Die Punkte \(P\) und \(Q\) liegen symmetrisch zu einer Ebene \(F\). Ermitteln Sie eine Gleichung von \(F\).
(3 BE)
Lösung zu Teilaufgabe 1b
Parallele Ebenen
\[E \colon 2x_{1} + x_{2} + 2x_{3} = 6\]
\(P(1|0|2)\), \(Q(5|2|6)\)
![Ebene E und parallele Ebene F durch den Mittelpunkt der Strecke [PQ] Ebene E und parallele Ebene F durch den Mittelpunkt der Strecke [PQ]](/images/stories/B2016_PT_A_G_2/B2016_PT_A_G_2_1b.png)
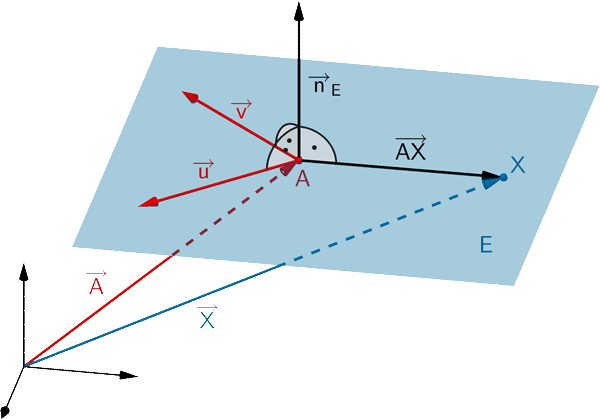
Planskizze: Ebene \(E\) und Ebene \(F \parallel E\) durch den Mittelpunkt \(M_{[PQ]}\) der Strecke \([PQ]\)
Die Punkte \(P\) und \(Q\) liegen symmetrisch zur Ebene \(F\), wenn die Gerade \(PQ\) senkrecht zur Ebene \(F\) verläuft und die Ebene \(F\) den Mittelpunkt \(M_{[PQ]}\) der Strecke \([PQ]\) enthält.
\[\left. \begin{align*} &PQ \perp E \\[0.8em] &PQ \perp F \end{align*} \right\} \quad \Longrightarrow \quad F \parallel E \quad \Longrightarrow \quad \overrightarrow{n}_{F} = \overrightarrow{n}_{E}\]
Ebenengleichung in Normalenform (vgl. Merkhilfe)
Jede Ebene lässt sich durch eine Gleichung in Normalenform beschreiben. Ist \(A\) ein beliebiger Aufpunkt der Ebene \(E\) und \(\overrightarrow{n}_{E}\) ein Normalenvektor von \(E\), so erfüllt jeder Punkt \(X\) der Ebene \(E\) folgende Gleichungen:
Normalenform in Vektordarstellung
\[E \colon \overrightarrow{n}_{E} \circ (\overrightarrow{X} - \overrightarrow{A}) = 0\]
Normalenform in Koordinatendarstellung
\[E \colon n_{1}x_{1} + n_{2}x_{2} + n_{3}x_{3} + n_{0} = 0\]
mit \(n_{0} = -(\overrightarrow{n}_{E} \circ \overrightarrow{A}) = - \: n_{1}a_{1} - n_{2}a_{2} - n_{3}a_{3}\)
\(n_{1}\), \(n_{2}\) und \(n_{3}\): Koordinaten eines Normalenvektors \(\overrightarrow{n}_{E}\)
\[F \colon \overrightarrow{n}_{E} \circ \left( \overrightarrow{X} - \overrightarrow{M}_{[PQ]} \right) = 0\]
Aus Teilaufgabe 1a ist bekannt:
\[\overrightarrow{n}_{E} = \begin{pmatrix} 2 \\ 1 \\ 2 \end{pmatrix} = \overrightarrow{n}_{F}\]
Ortsvektor \(\overrightarrow{M}_{[PQ]}\) berechnen:
Mittelpunkt einer Strecke
Für den Ortsvektor \(\overrightarrow{M}\) des Mittelpunkts \(M\) einer Strecke \([AB]\) gilt:
\[\overrightarrow{M} = \frac{1}{2} \left( \overrightarrow{A} + \overrightarrow{B} \right)\]
\[\begin{align*}\overrightarrow{M}_{[PQ]} &= \frac{1}{2} \cdot (\overrightarrow{P} + \overrightarrow{Q}) \\[0.8em] &= \frac{1}{2} \cdot \left[ \begin{pmatrix} 1 \\ 0 \\ 2 \end{pmatrix} + \begin{pmatrix} 5 \\ 2 \\ 6 \end{pmatrix} \right] \\[0.8em] &= \frac{1}{2} \cdot \begin{pmatrix} 6 \\ 2 \\ 8 \end{pmatrix} \\[0.8em] &= \begin{pmatrix} 3 \\ 1 \\ 4 \end{pmatrix} \end{align*}\]
Damit lässt sich die Ebene \(F\) in der Normalenform in Vektordarstellung angeben. Eine Umformung in die Kordiantendarstellung kann erfolgen, ist aber nicht zwingend erforderlich, da die Aufgabenstellung dies nicht ausdrücklich verlangt.
Ebenengleichung in Normalenform (vgl. Merkhilfe)
Jede Ebene lässt sich durch eine Gleichung in Normalenform beschreiben. Ist \(A\) ein beliebiger Aufpunkt der Ebene \(E\) und \(\overrightarrow{n}_{E}\) ein Normalenvektor von \(E\), so erfüllt jeder Punkt \(X\) der Ebene \(E\) folgende Gleichungen:
Normalenform in Vektordarstellung
\[E \colon \overrightarrow{n}_{E} \circ (\overrightarrow{X} - \overrightarrow{A}) = 0\]

Normalenform in Koordinatendarstellung
\[E \colon n_{1}x_{1} + n_{2}x_{2} + n_{3}x_{3} + n_{0} = 0\]
mit \(n_{0} = -(\overrightarrow{n}_{E} \circ \overrightarrow{A}) = - \: n_{1}a_{1} - n_{2}a_{2} - n_{3}a_{3}\)
\(n_{1}\), \(n_{2}\) und \(n_{3}\): Koordinaten eines Normalenvektors \(\overrightarrow{n}_{E}\)
\[F \colon \overrightarrow{n}_{E} \circ \left( \overrightarrow{X} - \overrightarrow{M}_{[PQ]} \right) = 0\]
\[F \colon \begin{pmatrix} 2 \\ 1 \\ 2 \end{pmatrix} \circ \left[ \overrightarrow{X} - \begin{pmatrix} 3 \\ 1 \\ 4 \end{pmatrix} \right] = 0\]
Umformung in die Koordinatendarstellung (nicht verlangt!):
Skalarprodukt
Unter dem Skalarprodukt \(\overrightarrow{a} \circ \overrightarrow{b}\) zweier Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) versteht man das Produkt aus den Beträgen der beiden Vektoren und dem Kosinus des von den Vektoren eingeschlossenen Winkels \(\varphi\).
\[\overrightarrow{a} \circ \overrightarrow{b} = \vert \overrightarrow{a} \vert \cdot \vert \overrightarrow{b} \vert \cdot \cos{\varphi} \quad (0^{\circ} \leq \varphi \leq 180^{\circ})\]
Berechnung eines Skalarprodukts im \(\boldsymbol{\mathbb R^{3}}\) (vgl. Merkhilfe)
\[\overrightarrow{a} \circ \overrightarrow{b} = \begin{pmatrix} a_{1} \\ a_{2} \\ a_{3} \end{pmatrix} \circ \begin{pmatrix} b_{1} \\ b_{2} \\ b_{3} \end{pmatrix} = a_{1}b_{1} + a_{2}b_{2} + a_{3}b_{3}\]
\[\begin{align*}\begin{pmatrix} 2 \\ 1 \\ 2 \end{pmatrix} \circ \left[ \overrightarrow{X} - \begin{pmatrix} 3 \\ 1 \\ 4 \end{pmatrix} \right] &= 0 \\[0.8em] 2 \cdot (x_{1} - 3) + 1 \cdot (x_{2} - 1) + 2 \cdot (x_{3} - 4) &= 0 \\[0.8em] 2x_{1} - 6 + x_{2} - 1 + 2x_{3} - 8 &= 0 \\[0.8em] 2x_{1} + x_{2} + 2x_{3} - 15 &= 0 \end{align*}\]
\[\Longrightarrow \quad F \colon 2x_{1} + x_{2} + 2x_{3} = 15\]


