Untersuchen Sie, ob \(K\) die \(x_1x_2\)-Ebene schneidet.
(2 BE)
Lösung zu Teilaufgabe b
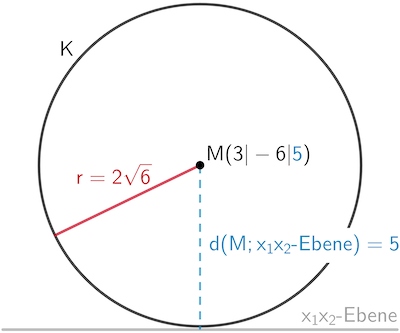
Planskizze (optional): Der Abstand \(\textcolor{#0087c1}{d(M;x_1x_2\text{-Ebene})}\) des Mittelpunkts \(M\) der Kugel \(K\) von der \(x_1x_2\)-Ebene lässt sich der \(\textcolor{#0087c1}{x_3}\)-Koordinate von \(M\) entnehmen.
Da \(\textcolor{#cc071e}{r = 2\sqrt{6} = \sqrt{24}} \boldsymbol{<} \textcolor{#0087c1}{\sqrt{25} = 5 = d(M;x_1x_2\text{-Ebene})}\) gilt, schneidet die Kugel \(K\) nicht die \(x_1x_2\)-Ebene.
Alternative: Lotfußpunktverfahren
Die Bestimmung des Abstands des Mittelpunkts \(M\) der Kugel \(K\) von der \(x_1x_2\)-Ebene mithilfe des Lotfußpunktverfahrens ist im Falle der vorliegenden Thematik Abstand Punkt - Koordinatenebene eigentlich zu aufwendig (vgl. Abiturskript - 2.4.4 Abstand Punkt - Ebene, Lotfußpunktverfahren). Der Vollständigkeit halber sei dieser Lösungsansatz dennoch aufgeführt.
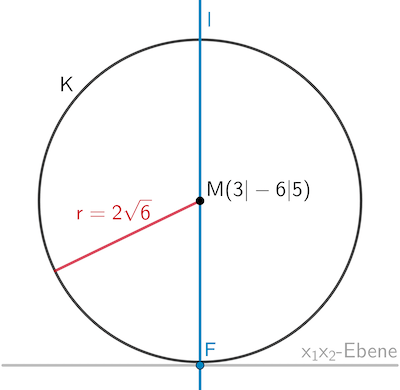
Planskizze (optional): Die Lotgerade \(\textcolor{#0087c1}{l}\) durch den Kugelmittelpunkt \(M\) auf die \(x_1x_2\)-Ebene schneidet die \(x_1x_2\)-Ebene im Lotfußpunkt \(\textcolor{#0087c1}{F}\). Für den Abstand des Kugelmittelpunkts \(M\) von der \(x_1x_2\)-Ebene gilt:
\[d(M;x_1x_2\text{-Ebene}) = \vert \overrightarrow{\textcolor{#0087c1}{F}M} \vert\]
Gleichung der Lotgerade \(\textcolor{#0087c1}{l}\) formulieren:
Der Normalenvektor \(\overrightarrow{n} = \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix}\) ist ein Richtungsvektor der Lotgerade \(\textcolor{#0087c1}{l}\).
Lotgerade auf eine Ebene
\[E\,\colon \overrightarrow{n}_E \circ (\overrightarrow{X} - \overrightarrow{A}) = 0; \quad P\,(p_1|p_2|p_3)\]
Die Lotgerade \(\ell\) mit \(P \in \ell\) auf eine Ebene \(E\) ist durch den Ortsvektor \(\overrightarrow{P}\) und den Normalenvektor \(\overrightarrow{n}_E\) eindeutig bestimmt:
\[\ell\,\colon \overrightarrow{X} = \overrightarrow{P} + \lambda \cdot \overrightarrow{n}_E; \; \lambda \in \mathbb R\]
\[\textcolor{#0087c1}{l \colon \overrightarrow{X} = \overrightarrow{M} + \lambda \cdot \overrightarrow{n}, \; \lambda \in \mathbb R}\]
\[l \colon \overrightarrow{X} = \begin{pmatrix} 3 \\ -6 \\ 5 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix}, \; \lambda \in \mathbb R \]
Eine Gleichung der \(x_1x_2\)-Ebene in Normalenform in Koordinatendarstellung (Koordinatenform) lautet: \(x_3 = 0\).
Lotfußpunkt \(\textcolor{#0087c1}{F}\) bestimmen:
Hierfür werden die Koordinaten des Ortsvektors \(X\) der Gleichung der Lotgerade \(l\) in die Gleichung der \(x_1x_2\)-Ebene eingesetzt (hier nur \(x_3\)-Koordinate) und diese nach \(\lambda\) aufgelöst.
\[l \colon \overrightarrow{X} = \begin{pmatrix} 3 \\ -6 \\ \textcolor{#e9b509}{5} \end{pmatrix} + \textcolor{#e9b509}{\lambda} \cdot \begin{pmatrix} 0 \\ 0 \\ \textcolor{#e9b509}{1} \end{pmatrix}, \; \lambda \in \mathbb R \]
\[x_1x_2\text{-Ebene} \colon x_3 = 0\]
\[\begin{align*}l \cap x_1x_2\text{-Ebene} \colon \textcolor{#e9b509}{5} + \textcolor{#e9b509}{\lambda} \cdot \textcolor{#e9b509}{1} &= 0 &&| -5 \\[0.8em] \lambda &= -5 \end{align*}\]
\(\textcolor{#89ba17}{\lambda = -5}\) in die Gleichung der Lotgerade \(\textcolor{#0087c1}{l}\) eingesetzt, ergibt den Ortsvektor \(\textcolor{#0087c1}{\overrightarrow{F}}\) des Lotfußpunkts \(\textcolor{#0087c1}{F}\).
\[\textcolor{#0087c1}{F \in l} \colon \textcolor{#0087c1}{\overrightarrow{F}} = \begin{pmatrix} 3 \\ -6 \\ 5 \end{pmatrix} + \textcolor{#89ba17}{(-5)} \cdot \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} = \textcolor{#0087c1}{\begin{pmatrix} 3 \\ -6 \\ 0 \end{pmatrix}}\]
Abstand des Kugelmittelpunkts \(M\) von der \(x_1x_2\)-Ebene berechnen:
Betrag eines Vektors
\[ \vert \overrightarrow{a} \vert = \sqrt{\overrightarrow{a} \circ \overrightarrow{a}} = \sqrt{{a_1}^2 + {a_2}^2 + {a_3}^2}\]
(vgl. Merkhilfe)
\[\begin{align*}d(M;x_1x_2\text{-Ebene}) &= \vert \overrightarrow{\textcolor{#0087c1}{F}M} \vert = \vert \overrightarrow{M} - \textcolor{#0087c1}{\overrightarrow{F}} \vert \\[0.8em] &= \left|\begin{pmatrix} 3 \\ -6 \\ 5 \end{pmatrix} - \textcolor{#0087c1}{\begin{pmatrix} 3 \\ -6 \\ 0 \end{pmatrix}} \right| = \left| \begin{pmatrix} 0 \\ 0 \\ 5 \end{pmatrix} \right| \\[0.8em] &= \sqrt{0^2 + 0^2 + 5^2} = \sqrt{25} = 5 \end{align*}\]
Da \(\textcolor{#cc071e}{r = 2\sqrt{6} = \sqrt{24}} \boldsymbol{<} \sqrt{25} = 5 = d(M;x_1x_2\text{-Ebene})\) gilt, schneidet die Kugel \(K\) nicht die \(x_1x_2\)-Ebene.


