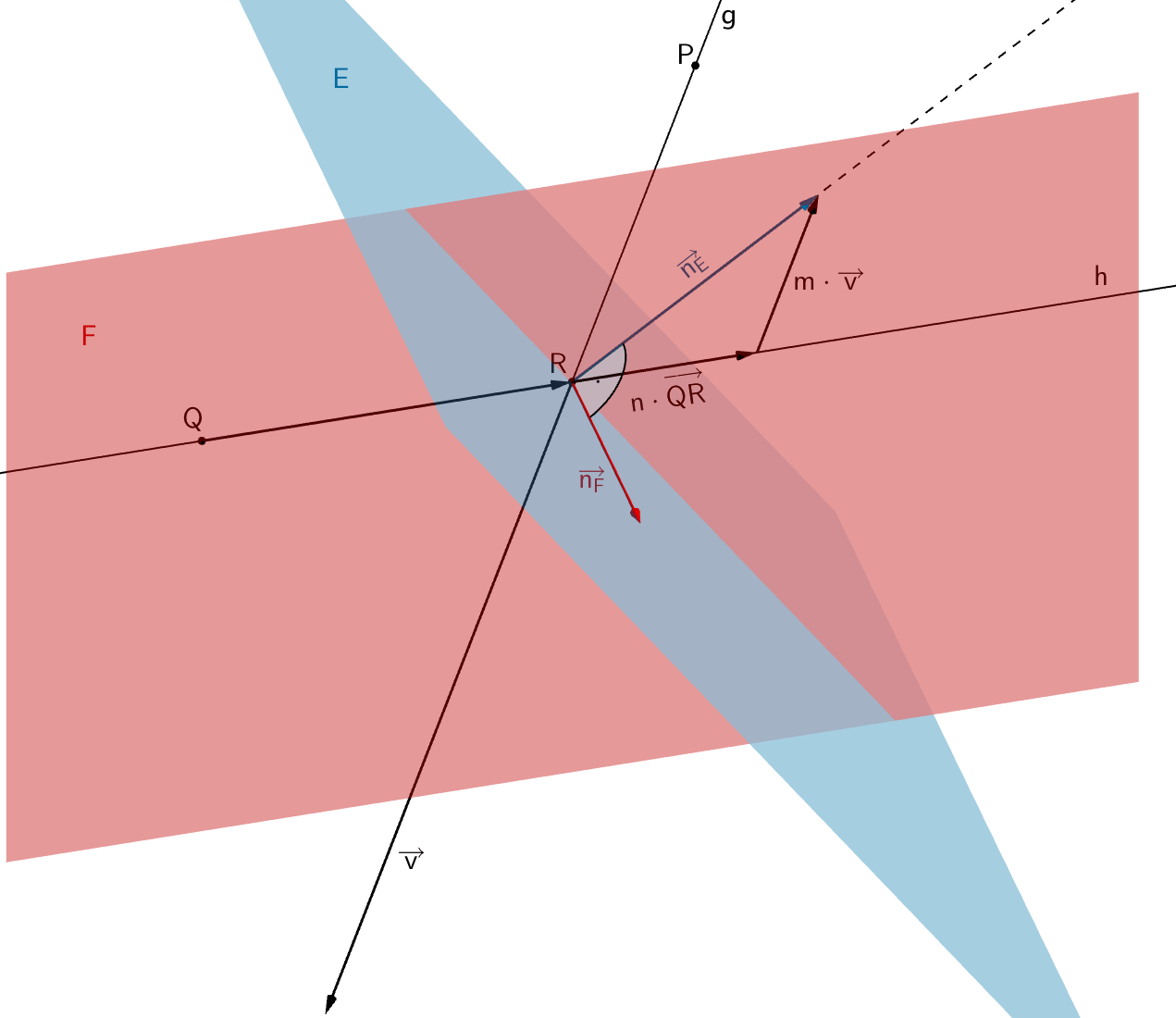
Das Lot zur Ebene \(E\) im Punkt \(R\) wird als Einfallslot bezeichnet.
Die beiden Geraden, entlang derer der einfallende und der reflektierte Lichtstrahl im Modell verlaufen, liegen in einer Ebene \(F\). Ermitteln Sie eine Gleichung von \(F\) in Normalenform. Weisen Sie nach, dass das Einfallslot ebenfalls in der Ebene \(F\) liegt.
(mögliches Teilergebnis: \(F\,\colon\, x_1 - x_2 = 0\))
(5 BE)
Lösung zu Teilaufgabe d
Ebene \(E\), Ebene \(F\), Dreieck \(ABC\), Gerde \(g\) (einfallender Lichtstrahl) und Gerade \(h\) (reflektierter Lichtstrahl)
Es sei \(h\) die Gerade, entlang der im Modell der reflektierte Lichtstrahl verläuft.
Gleichung der Ebene \(F\) in Normalenform
\[g\,\colon\, \overrightarrow{X} = \overrightarrow{P} + \lambda \cdot \overrightarrow{v}\,; \enspace \lambda \in \mathbb R \]
\[h\,\colon\,\overrightarrow{X} = \overrightarrow{Q} + \tau \cdot \overrightarrow{QR}\,; \enspace \tau \in \mathbb R\]
Ebenengleichung in Normalenform (vgl. Merkhilfe)
Jede Ebene lässt sich durch eine Gleichung in Normalenform beschreiben. Ist \(A\) ein beliebiger Aufpunkt der Ebene \(E\) und \(\overrightarrow{n}_{E}\) ein Normalenvektor von \(E\), so erfüllt jeder Punkt \(X\) der Ebene \(E\) folgende Gleichungen:
Normalenform in Vektordarstellung
\[E \colon \overrightarrow{n}_{E} \circ (\overrightarrow{X} - \overrightarrow{A}) = 0\]

Normalenform in Koordinatendarstellung
\[E \colon n_{1}x_{1} + n_{2}x_{2} + n_{3}x_{3} + n_{0} = 0\]
mit \(n_{0} = -(\overrightarrow{n}_{E} \circ \overrightarrow{A}) = - \: n_{1}a_{1} - n_{2}a_{2} - n_{3}a_{3}\)
\(n_{1}\), \(n_{2}\) und \(n_{3}\): Koordinaten eines Normalenvektors \(\overrightarrow{n}_{E}\)
Die beiden Geraden \(g\) (einfallender Lichtstrahl) und \(h\) (reflektierter Lichtstrahl) legen die Ebene \(F\) fest, deren Gleichung in Parameterform mit \(Q\) als Aufpunkt lautet:
\[F\,\colon\, \overrightarrow{X} = \overrightarrow{Q} + \lambda \cdot \overrightarrow{v} + \tau \cdot \overrightarrow{QR}\,; \enspace \lambda, \tau \in \mathbb R\]
Mithilfe des Vektorprodukts aus den beiden Richtungsvektoren \(\overrightarrow{v}\) und \(\overrightarrow{QR}\) der Gerden \(g\) bzw. \(h\) lässt sich der Normalenvektor \(\overrightarrow{n}_{F}\) für die Gleichung der Ebene \(F\) in Normalenform bestimmen.
Richtungsvektor \(\overrightarrow{QR}\) berechnen:
\[\overrightarrow{QR} = \overrightarrow{R} - \overrightarrow{Q} = \begin{pmatrix} 1{,}5 \\ 1{,}5 \\ 1 \end{pmatrix} - \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} = \begin{pmatrix} 1{,}5 \\ 1{,}5 \\ 0 \end{pmatrix}\]
Normalenvektor der Ebene \(F\) bestimmen:
\(\overrightarrow{v} = \begin{pmatrix} -1 \\ -1 \\ -4 \end{pmatrix}\) (siehe Teilaufgabe b)
\[\overrightarrow{QR} = \begin{pmatrix} 1{,}5 \\ 1{,}5 \\ 0 \end{pmatrix}\]
Vektorprodukt (Kreuzprodukt)
Das Vektorprodukt \(\overrightarrow{a} \times \overrightarrow{b}\) zweier Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) erzeugt einen neuen Vektor \(\overrightarrow{c} = \overrightarrow{a} \times \overrightarrow{b}\) mit den Eigenschaften:
\(\overrightarrow{c}\) ist sowohl zu \(\overrightarrow{a}\) als auch zu \(\overrightarrow{b}\) senkrecht.
\[\overrightarrow{c} = \overrightarrow{a} \times \overrightarrow{b} \quad \Longrightarrow \quad \overrightarrow{c} \perp \overrightarrow{a}, \enspace \overrightarrow{c} \perp \overrightarrow{b}\]
Der Betrag des Vektorprodukts zweier Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) ist gleich dem Produkt aus den Beträgen der Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) und dem Sinus des von ihnen eingeschlossenen Winkels \(\varphi\).
\[\vert \overrightarrow{a} \times \overrightarrow{b} \vert = \vert \overrightarrow{a} \vert \cdot \vert \overrightarrow{b} \vert \cdot \sin{\varphi} \quad (0^{\circ} \leq \varphi \leq 180^{\circ})\]
Die Vektoren \(\overrightarrow{a}\), \(\overrightarrow{b}\) und \(\overrightarrow{c}\) bilden in dieser Reihenfolge ein Rechtssystem. Rechtehandregel: Weist \(\overrightarrow{a}\) in Richtung des Daumens und \(\overrightarrow{b}\) in Richtung des Zeigefingers, dann weist \(\overrightarrow{c} = \overrightarrow{a} \times \overrightarrow{b}\) in Richtung des Mittelfingers.
Berechnung eines Vektorprodukts im \(\boldsymbol{\mathbb R^{3}}\) (vgl. Merkhilfe)
\[\overrightarrow{a} \times \overrightarrow{b} = \begin {pmatrix} a_1 \\ a_2 \\ a_3 \end {pmatrix} \times \begin {pmatrix} b_1 \\ b_2 \\ b_3 \end {pmatrix} = \begin {pmatrix} a_2 \cdot b_3 - a_3 \cdot b_2 \\ a_3 \cdot b_1 - a_1 \cdot b_3 \\ a_1 \cdot b_2 - a_2 \cdot b_1 \end {pmatrix}\]
\[\begin{align*} \overrightarrow{v} \times \overrightarrow{QR} &= \begin{pmatrix} -1 \\ -1 \\ -4 \end{pmatrix} \times \begin{pmatrix} 1{,}5 \\ 1{,}5 \\ 0 \end{pmatrix} \\[0.8em] &= \begin{pmatrix} (-1) & \cdot & 0 & - & (-4) & \cdot & 1{,}5 \\ (-4) & \cdot & 1{,}5 & - & (-1) & \cdot & 0 \\ (-1) & \cdot & 1{,}5 & - & (-1) & \cdot & 1{,}5 \end{pmatrix} \\[0.8em] &= \begin{pmatrix} 6 \\ -6 \\ 0 \end{pmatrix} = 6 \cdot \begin{pmatrix} 1 \\ -1 \\ 0 \end{pmatrix} \end{align*}\]
\[\Longrightarrow \quad \overrightarrow{n}_{F} = \begin{pmatrix} 1 \\ -1 \\ 0 \end{pmatrix}\]
Gleichung der Ebene \(F\) in Normalenform in Vektordarstellung:
Es sei \(Q\) der Aufpunkt der Ebene \(F\).
\[\begin{align*} F\,\colon\, \overrightarrow{n}_{F} \circ \bigg( \overrightarrow{X} - \overrightarrow{Q} \bigg) &= 0 \\[0.8em] \begin{pmatrix} 1 \\ -1 \\ 0 \end{pmatrix} \circ \left[ \overrightarrow{X} - \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} \right] &= 0\end{align*}\]
Gleichung der Ebene \(F\) in Normalenform in Koordinatendarstellung:
Skalarprodukt
Unter dem Skalarprodukt \(\overrightarrow{a} \circ \overrightarrow{b}\) zweier Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) versteht man das Produkt aus den Beträgen der beiden Vektoren und dem Kosinus des von den Vektoren eingeschlossenen Winkels \(\varphi\).
\[\overrightarrow{a} \circ \overrightarrow{b} = \vert \overrightarrow{a} \vert \cdot \vert \overrightarrow{b} \vert \cdot \cos{\varphi} \quad (0^{\circ} \leq \varphi \leq 180^{\circ})\]
Berechnung eines Skalarprodukts im \(\boldsymbol{\mathbb R^{3}}\) (vgl. Merkhilfe)
\[\overrightarrow{a} \circ \overrightarrow{b} = \begin{pmatrix} a_{1} \\ a_{2} \\ a_{3} \end{pmatrix} \circ \begin{pmatrix} b_{1} \\ b_{2} \\ b_{3} \end{pmatrix} = a_{1}b_{1} + a_{2}b_{2} + a_{3}b_{3}\]
\[\begin{align*} \begin{pmatrix} 1 \\ -1 \\ 0 \end{pmatrix} \circ \left[ \overrightarrow{X} - \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} \right] &= 0 \\[0.8em] 1 \cdot (x_{1} - 0) + (-1) \cdot (x_{2} - 0) + 0 \cdot (x_{3} - 1) &= 0 \\[0.8em] x_{1} - x_{2} &= 0 \end{align*}\]
\[F\,\colon\, x_{1} - x_{2} = 0\]
Es ist ebenso möglich, direkt mit der Normalenform in Koordinatendarstellung anzusetzen.
Ebenengleichung in Normalenform (vgl. Merkhilfe)
Jede Ebene lässt sich durch eine Gleichung in Normalenform beschreiben. Ist \(A\) ein beliebiger Aufpunkt der Ebene \(E\) und \(\overrightarrow{n}_{E}\) ein Normalenvektor von \(E\), so erfüllt jeder Punkt \(X\) der Ebene \(E\) folgende Gleichungen:
Normalenform in Vektordarstellung
\[E \colon \overrightarrow{n}_{E} \circ (\overrightarrow{X} - \overrightarrow{A}) = 0\]

Normalenform in Koordinatendarstellung
\[E \colon n_{1}x_{1} + n_{2}x_{2} + n_{3}x_{3} + n_{0} = 0\]
mit \(n_{0} = -(\overrightarrow{n}_{E} \circ \overrightarrow{A}) = - \: n_{1}a_{1} - n_{2}a_{2} - n_{3}a_{3}\)
\(n_{1}\), \(n_{2}\) und \(n_{3}\): Koordinaten eines Normalenvektors \(\overrightarrow{n}_{E}\)
\[\overrightarrow{n}_{F} = \begin{pmatrix} 1 \\ -1 \\ 0 \end{pmatrix}\]
\(Q\,(0|0|1) \in F\,\) (Aufpunkt)
\[\begin{align*}F\,\colon & & n_{1}x_{1} + n_{2}x_{2} + n_{3}x_{3} + n_{0} &= 0 & & (\text{mit} \; n_{0} = -n_{1}q_{1} - n_{2}q_{2} - n_{3}q_{3}) \\[0.8em] & & 1 \cdot x_{1} + (-1) \cdot x_{2} + 0 \cdot x_{3} + n_{0} &= 0 \\[0.8em] & & x_{1} - x_{2} + n_{0} &= 0 \end{align*}\]
\[\begin{align*}Q \in F\,\colon\, 0 - 0 + n_{0} &= 0 \\[0.8em] n_{0} &= 0\end{align*}\]
\[F\,\colon\,x_{1} - x_{2} = 0\]
Nachweis, dass das Einfallslot ebenfalls in der Ebene \(F\) liegt
Der Richtungsvektor des Einfallslots ist gleich dem Normalenvektor der Ebene \(E\). Lässt sich dieser als Linearkombination der Richtungsvektoren der Geraden \(g\) (einfallender Lichtstrahl) und \(h\) (reflektierter Lichtstrahl) beschreiben (komplanare Vektoren), liegt das Einfallslot in der Ebene \(F\).
Der Normalenvektor der Ebene \(F\) ist senkrecht zum Richtungsvektor von \(g\) und zum Richtungsvektor von \(h\). Liegt das Einfallslot in der Ebene \(F\), muss der Richtungsvektor des Einfallslots (Normalenvektor der Ebene \(E\)) ebenfalls senkrecht zum Normalenvektor der Ebene \(F\) sein.
1. Lösungsansatz: Linearkombination der Richtungsvektoren
Wenn \(\overrightarrow{n}_{E} = m \cdot \overrightarrow{v} + n \cdot \overrightarrow{QR}\,; \enspace m,n \in \mathbb R\) gilt, liegt das Einfallslot in der Ebene \(F\).
\(\overrightarrow{n}_{E} = \begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix};\;\) \(\overrightarrow{v} = \begin{pmatrix} -1 \\ -1 \\ -4 \end{pmatrix};\;\) \(\overrightarrow{OR} = \begin{pmatrix} 1{,}5 \\ 1{,}5 \\ 0 \end{pmatrix}\) (siehe Teilaufgaben b,c,d)
\[\begin{align*} \overrightarrow{n}_{E} &= m \cdot \overrightarrow{v} + n \cdot \overrightarrow{QR} \\[0.8em] \begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix} &= m \cdot \begin{pmatrix} -1 \\ -1 \\ -4 \end{pmatrix} + n \cdot \begin{pmatrix} 1{,}5 \\ 1{,}5 \\ 0 \end{pmatrix} \end{align*}\]
Lineares Gleichungssystem lösen:
\[\begin{align*} \text{I} & & & & 1 &= -m + 1{,}5n \\[0.8em] \text{II} & & & \wedge & 1 &= -m + 1{,}5n \\[0.8em] \text{III} & & & \wedge & 1 &= -4m & & \Longrightarrow \quad m = -\frac{1}{4} \end{align*}\]
\[\begin{align*}m = -\frac{1}{4} \; \text{in I}\,\colon\enspace 1 &= - \left( -\frac{1}{4} \right) + 1{,}5n \\[0.8em] 1 &= \frac{1}{4} + 1{,}5n & &| -\frac{1}{4} \\[0.8em] \frac{3}{4} &= 1{,}5n & &| : 1{,}5 \\[0.8em] \frac{1}{2} &= n \end{align*}\]
Eine Probe in II ist nicht notwendig, da die 1. und die 2. Gleichung übereinstimmen.
\[\Longrightarrow \quad \overrightarrow{n}_{E} = -\frac{1}{4} \cdot \overrightarrow{v} + \frac{1}{2} \cdot \overrightarrow{QR}\]
\(\Longrightarrow \quad\) Das Einfallslot liegt in der Ebene \(F\)
2. Löungsansatz: Orthogonale Normalenvektoren
Anwendung des Skalarprodukts:
Orthogonale (zueinander senkrechte) Vektoren (vgl. Merkhilfe)
\[\overrightarrow{a} \perp \overrightarrow{b} \; \Leftrightarrow \; \overrightarrow{a} \circ \overrightarrow{b} \quad (\overrightarrow{a} \neq \overrightarrow{0},\; \overrightarrow{b} \neq \overrightarrow{0})\]
Sind der Richtungvektor des Einfallslots (Normalenvektor der Ebene \(E\)) und der Normalenvektor der Ebene \(F\) zueinander senkrecht, liegt das Einfallslot in der Ebene \(F\).
\[\overrightarrow{n}_{E} \circ \overrightarrow{n}_{F} = 0 \quad \Longleftrightarrow \quad \overrightarrow{n}_{E} \perp \overrightarrow{n}_{F}\]
Skalarprodukt
Unter dem Skalarprodukt \(\overrightarrow{a} \circ \overrightarrow{b}\) zweier Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) versteht man das Produkt aus den Beträgen der beiden Vektoren und dem Kosinus des von den Vektoren eingeschlossenen Winkels \(\varphi\).
\[\overrightarrow{a} \circ \overrightarrow{b} = \vert \overrightarrow{a} \vert \cdot \vert \overrightarrow{b} \vert \cdot \cos{\varphi} \quad (0^{\circ} \leq \varphi \leq 180^{\circ})\]
Berechnung eines Skalarprodukts im \(\boldsymbol{\mathbb R^{3}}\) (vgl. Merkhilfe)
\[\overrightarrow{a} \circ \overrightarrow{b} = \begin{pmatrix} a_{1} \\ a_{2} \\ a_{3} \end{pmatrix} \circ \begin{pmatrix} b_{1} \\ b_{2} \\ b_{3} \end{pmatrix} = a_{1}b_{1} + a_{2}b_{2} + a_{3}b_{3}\]
\(\overrightarrow{n}_{E} = \begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix};\;\) \(\overrightarrow{n}_{F} = \begin{pmatrix} 1 \\ -1 \\ 0 \end{pmatrix};\;\) (siehe Teilaufgaben b,d)
\[\begin{align*} \overrightarrow{n}_{E} \circ \overrightarrow{n}_{F} &= 0 \\[0.8em] \begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix} \circ \begin{pmatrix} 1 \\ -1 \\ 0 \end{pmatrix} &= 0 \\[0.8em] 1 \cdot 1 + 1 \cdot (-1) + 1 \cdot 0 &= 0 \\[0.8em] 0 &= 0 \quad (w) \end{align*}\]
\[\Longrightarrow \quad \overrightarrow{n}_{E} \perp \overrightarrow{n}_{F}\]
\(\Longrightarrow \quad\) Das Einfallslot liegt in der Ebene \(F\)