- Details
- Kategorie: Geometrie 1
Die Abbildung 1 zeigt modellhaft eine Mehrzweckhalle, die auf einer horizontalen Fläche steht und die Form eines geraden Prismas hat.
Die Punkte \(A_{1}(0|0|0)\), \(A_{2}(20|0|0)\), \(A_{3}\) und \(A_{4}(0|10|0)\) stellen im Modell die Eckpunkte der Grundfläche der Mehrzweckhalle dar, die Punkte \(B_{1}\), \(B_{2}\), \(B_{3}\) und \(B_{4}\) die Eckpunkte der Dachfläche. Diejenige Seitenwand, die im Modell in der \(x_{1}x_{3}\)-Ebene liegt, ist 6 m hoch, die ihr gegenüberliegende Wand nur 4 m.
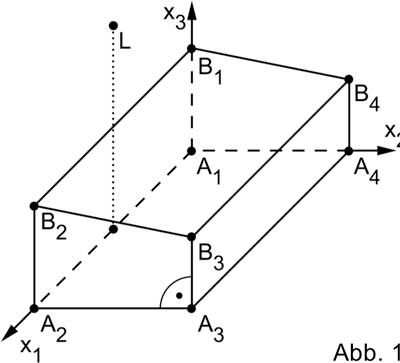
Eine Längeneinheit im Koordinatensystem entspricht 1 m, d.h. die Mehrzweckhalle ist 20 m lang.
Geben Sie die Koordinaten der Punkte \(B_{2}\), \(B_{3}\) und \(B_{4}\) an und bestätigen Sie, dass diese Punkte in der Ebene \(E \colon x_{2} + 5x_{3} - 30 = 0\) liegen.
(4 BE)
- Details
- Kategorie: Geometrie 1
Berechnen Sie die Größe des Neigungswinkels der Dachfläche gegenüber der Horizontalen.
(3 BE)
- Details
- Kategorie: Geometrie 1
Der Punkt \(T(7|10|0)\) liegt auf der Kante \([A_{3}A_{4}]\). Untersuchen Sie rechnerisch, ob es Punkte auf der Kante \([B_{3}B_{4}]\) gibt, für die gilt: Die Verbindungsstrecken des Punktes zu den Punkten \(B_{1}\) und \(T\) stehen aufeinander senkrecht. Geben Sie gegebenenfalls die Koordinaten dieser Punkte an.
(6 BE)
- Details
- Kategorie: Geometrie 1
Der Punkt \(L\), der vertikal über dem Mittelpunkt der Kante \([A_{1}A_{2}]\) liegt, veranschaulicht im Modell die Position einer Flutlichtanlage, die 12 m über der Grundfläche angebracht ist. Die als punktförmig angenommene Lichtquelle beleuchtet - mit Ausnahme des Schattenbereichs in der Nähe der Hallenwände - das gesamte Gelände um die Halle.
Die Punkte \(L\), \(B_{2}\) und \(B_{3}\) legen eine Ebene \(F\) fest. Ermitteln Sie eine Gleichung von \(F\) in Normalenform.
(zur Kontrolle: \(F \colon 3x_{1} + x_{2} + 5x_{3} - 90 = 0\))
(5 BE)
- Details
- Kategorie: Geometrie 1
Die Ebene \(F\) schneidet die \(x_{1}x_{2}\)-Ebene in der Geraden \(g\). Bestimmen Sie eine Gleichung von \(g\).
(zur Kontrolle: \(g \colon \overrightarrow{X} = \begin{pmatrix} 30 \\ 0 \\ 0 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 1 \\ -3 \\ 0 \end{pmatrix}, \; \lambda \in \mathbb R\))
(3 BE)
- Details
- Kategorie: Geometrie 1
Die Abbildung 2 zeigt den Grundriss des Hallenmodells in der \(x_{1}x_{2}\)-Ebene. Stellen Sie unter Verwendung der bisherigen Ergebnisse den Schattenbereich der Flutlichtanlage in der Abbildung exakt dar.
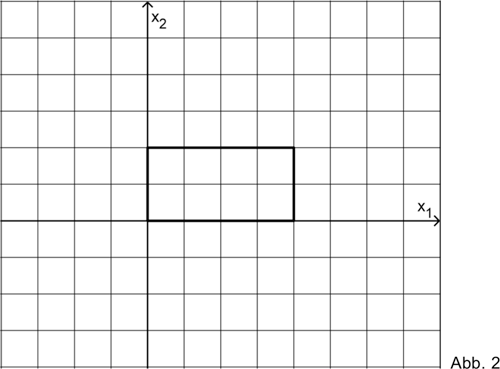
(4 BE)


