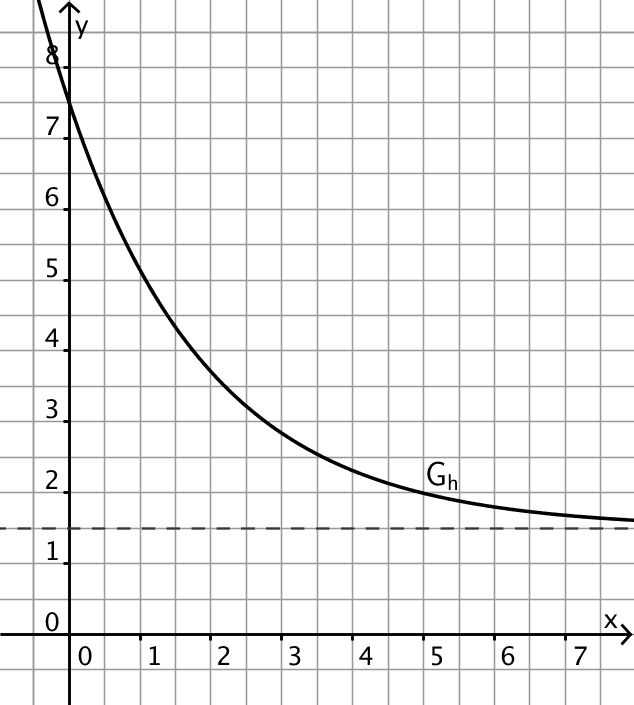
Gegeben ist die in \(\mathbb R\) definierte Funktion \(h : x \mapsto 6 \cdot e^{-0{,}5x} + 1{,}5\). Die Abbildung zeigt den in \(\mathbb R\) streng monoton fallenden Graphen \(G_h\) von \(h\) sowie dessen Asymptote, die durch die Gleichung \(y = 1{,}5\) gegeben ist.
Beschreiben Sie, wie \(G_h\) aus dem Graphen der in \(\mathbb R\) definierten natürlichen Exponentialfunktion \(x \mapsto e^x\) hervorgeht.
(4 BE)
Lösung zu Teilaufgabe 2a
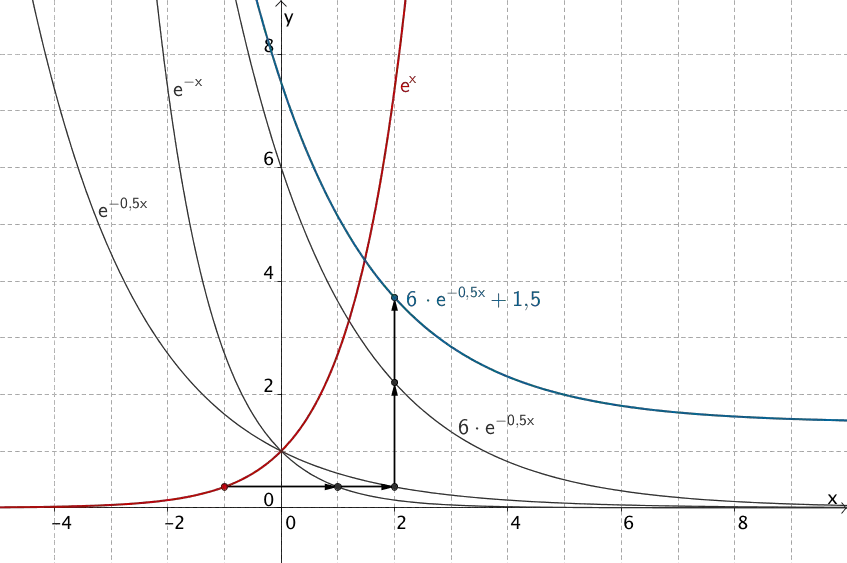
\(h(x) = 6 \cdot e^{-0{,}5x} + 1{,}5\)
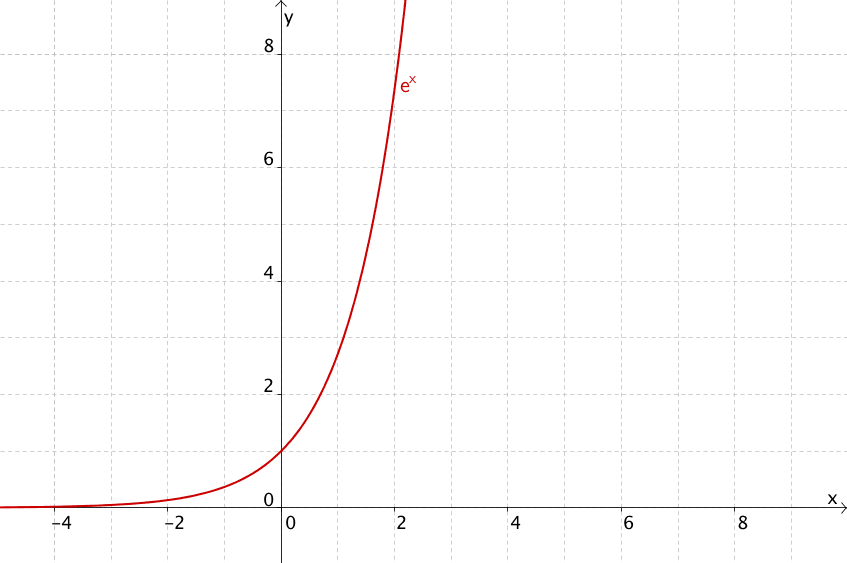
Natürliche Exponentialfunktion \(x \mapsto e^x\)
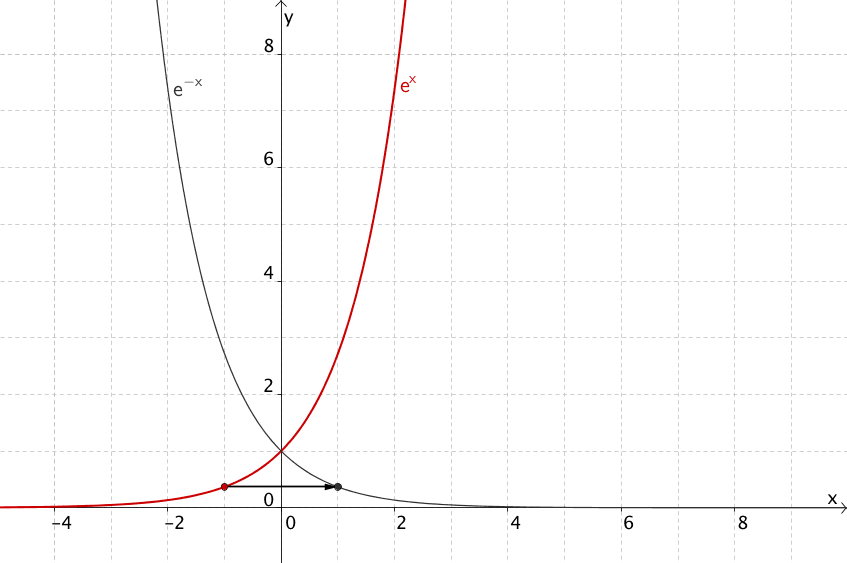
1. Spiegelung an der \(y\)-Achse
Spiegeln von Funktionsgraphen
Spiegelung an der \(x\)-Achse: \(g(x) = -f(x)\)
Spiegelung an der \(y\)-Achse: \(h(x) = f(-x)\)
\[\Rightarrow x \mapsto e^{-x}\]
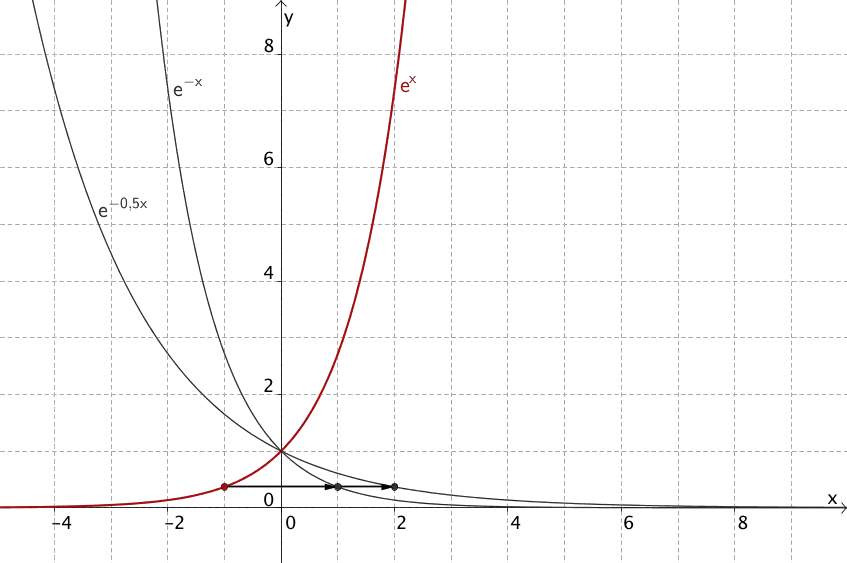
2. Streckung in \(x\)-Richtung mit Streckungsfaktor 2 \((k = \frac{1}{2})\)
Strecken von Funktionsgraphen
Streckung in \(\textcolor{#0087c1}{x}\)-Richtung mit Streckungsfaktor \(\textcolor{#0087c1}{k}\,\):
\[h(x) = f\left(\textcolor{#0087c1}{\frac{1}{k}} \cdot x \right), \enspace k > 0\]
Streckung in \(\textcolor{#0087c1}{x}\)-Richtung mit Streckungsfaktor \(\textcolor{#0087c1}{\dfrac{1}{k}}\):
\[h(x) = f(\textcolor{#0087c1}{k} \cdot x), \enspace k > 0\]
Streckung in \(\textcolor{#cc071e}{y}\)-Richtung mit Streckungsfaktor \(\textcolor{#cc071e}{k}\,\):
\[g(x) = \textcolor{#cc071e}{k} \cdot f(x), \enspace k > 0\]
\[\Rightarrow x \mapsto e^{-0{,}5x}\]
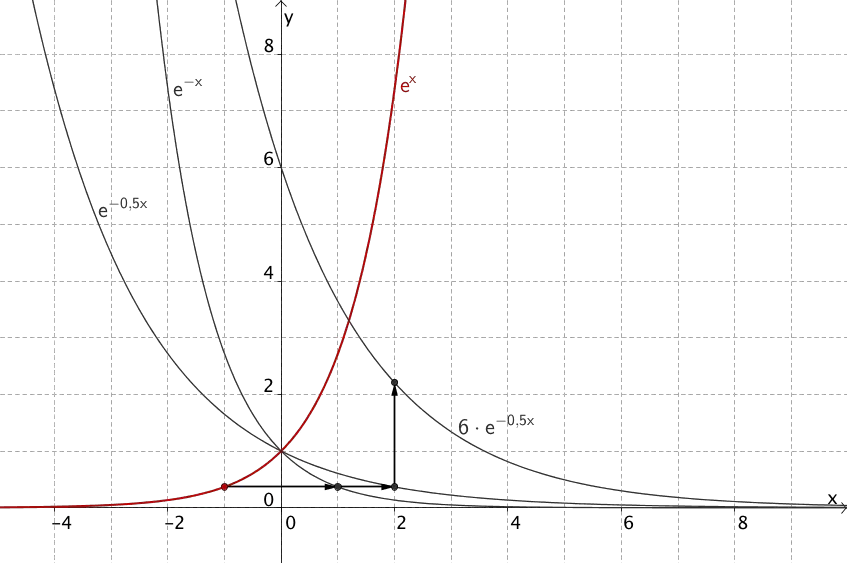
3. Streckung in \(y\)-Richtung mit Streckungsfaktor 6
Strecken von Funktionsgraphen
Streckung in \(\textcolor{#0087c1}{x}\)-Richtung mit Streckungsfaktor \(\textcolor{#0087c1}{k}\,\):
\[h(x) = f\left(\textcolor{#0087c1}{\frac{1}{k}} \cdot x \right), \enspace k > 0\]
Streckung in \(\textcolor{#0087c1}{x}\)-Richtung mit Streckungsfaktor \(\textcolor{#0087c1}{\dfrac{1}{k}}\):
\[h(x) = f(\textcolor{#0087c1}{k} \cdot x), \enspace k > 0\]
Streckung in \(\textcolor{#cc071e}{y}\)-Richtung mit Streckungsfaktor \(\textcolor{#cc071e}{k}\,\):
\[g(x) = \textcolor{#cc071e}{k} \cdot f(x), \enspace k > 0\]
\[\Rightarrow x \mapsto 6 \cdot e^{-0{,}5x}\]
4. Verschiebung in \(y\)-Richtung um 1,5
Verschieben von Funktionsgraphen
\[g(x) = f(x +a) + b\]
Verschiebung in \(x\)-Richtung um \(-a\), Verschiebung in \(y\)-Richtung um \(b\)
\[\Rightarrow h \colon x \mapsto 6 \cdot e^{-0{,}5x} + 1{,}5\]
Entstehung des Graphen der Funktion \(h \colon x \mapsto 6 \cdot e^{-0{,}5x} + 1{,}5\) aus dem Graphen der natürlichen Exponentialfunktion \(x \mapsto e^{x}\)