Aufgabe 1
Bestimmen Sie jeweils die erste Ableitung der folgenden Funktionen, ohne anschließend zu vereinfachen.
a) \(f(x) = 2\sqrt{x} \cdot \cos(0{,}5x)\)
b) \(g(x) = \dfrac{\ln\left(\dfrac{1}{x^{3}}\right)}{2x + 3}\)
Aufgabe 2
Die Abbildung zeigt den Graphen \(G_{f}\) der Funktion \(f \colon x \mapsto 4 - 2e^{x - 4}\).
a) Geben Sie die Definitionsmenge der Funktion \(f\) an. Bestimmen Sie das Verhalten an den Rändern des Definitionsbereichs. Geben Sie die Wertemenge der Funktion \(f\) an.
b) Begründen Sie, dass die Funktion \(f\) umkehrbar ist.
c) Berechnen Sie die Umkehrfunktion \(f^{-1}\) der Funktion \(f\) und geben Sie die Definitions- und Wertemenge der Umkehrfunktion an. Skizzieren Sie den Graphen der Umkehrfunktion \(f^{-1}\) in das obige Koordinatensystem.
Aufgabe 3
Gegeben ist die Funktion \(f\colon x \mapsto 2(e^{x} - 1)^{2}\). Der Graph der Funktion \(f\) wird mit \(G_{f}\) bezeichnet.
a) Geben Sie die Definitionsmenge der Funktion \(f\) an.
b) Ermitteln Sie das Verhalten von \(f\) für \(x \to -\infty\) und \(x \to +\infty\). Geben Sie die Gleichungen aller Asymptoten von \(G_{f}\) an.
c) Weisen Sie nach, dass der Koordinatenursprung absoluter Tiefpunkt von \(G_{f}\) ist. Geben Sie die Wertemenge der Funktion \(f\) an.
Aufgabe 4
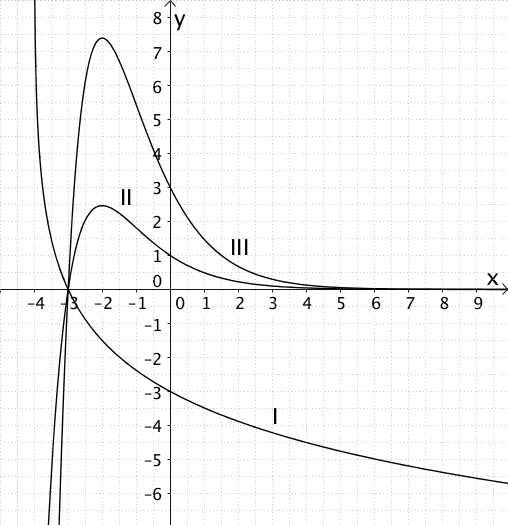
Einer der folgenden Graphen gehört zu der in \(\mathbb R\) definierten Funktion \(f \colon x \mapsto \dfrac{x + 3}{e^{x}}\). Der Graph der Funktion \(f\) wird mit \(G_{f}\) bezeichnet.
Geben Sie an, welcher der Graphen I, II oder III den Graphen \(G_{f}\) zeigt und begründen Sie jeweils, warum die beiden anderen Graphen nicht in Frage kommen.
Aufgabe 5
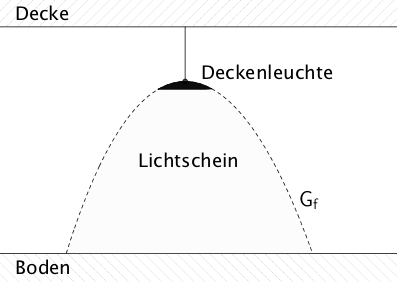
An der Decke eines Hausflurs ist eine Deckenleuchte angebracht. Die Randlinie des Lichtkegels der Deckenleuchte kann näherungsweise durch die Funktion \(\displaystyle f \colon x \mapsto -3 \cdot \left( e^{0{,}4x} + e^{-0{,}5x} \right) + 9\) beschrieben werden mit \(x\) und \(y\) in Metern (vgl. Abbildung). Der Graph der Funktion \(f\) wird mit \(G_{f}\) bezeichnet.
a) Zeigen Sie, dass \(G_{f}\) nicht symmetrisch bezüglich des Koordinatensystems ist.
b) Ersetzen Sie einen Zahl \((\neq 0)\) des Funktionsterms \(f(x)\) so, dass \(G_{f}\) symmetrisch ist und geben Sie die Art der Symmetrie an.
Eine Feinjustierung der LEDs der Deckenleuchte verändert den Lichtkegel. Die Randlinie des Lichtkegels wird nun näherungsweise durch die Funktion \(g \colon x \mapsto -3 \cdot \left( e^{0{,}5x} + e^{-0{,}5x} \right) + 9\) beschrieben. Der Graph der Funktion \(g\) wird mit \(G_{g}\) bezeichnet.
c) Bestimmen Sie die Schnittpunkte von \(G_{g}\) mit den Koordinatenachsen. Hinweis: Verwenden Sie die Substitution \(u = e^{0{,}5x}\) zur Bestimmung der Schnittpunkte mit der \(x\)-Achse.
d) Berechnen Sie den Winkel, unter dem \(G_{g}\) die negative \(x\)-Achse schneidet.
e) Die Position der Aufhängung der Deckenleuchte entspricht der Lage des Hochpunkts von \(G_{g}\). Die Aufhängung ist 85 cm von der Decke entfernt. Berechnen Sie die Raumhöhe \(h\) des Hausflurs, an dessen Decke die Deckenleuchte angebracht ist.
Aufgabe 6
Der Punkt \(A(4|-1|0)\) ist Mittelpunkt der Kugel \(K\), auf deren Oberfläche der Punkt \(B(-1|1|4)\) liegt.
Ermitteln Sie die Koordinaten eines weiteren Punktes \(C\), der ebenfalls auf der Kugeloberfläche liegt.