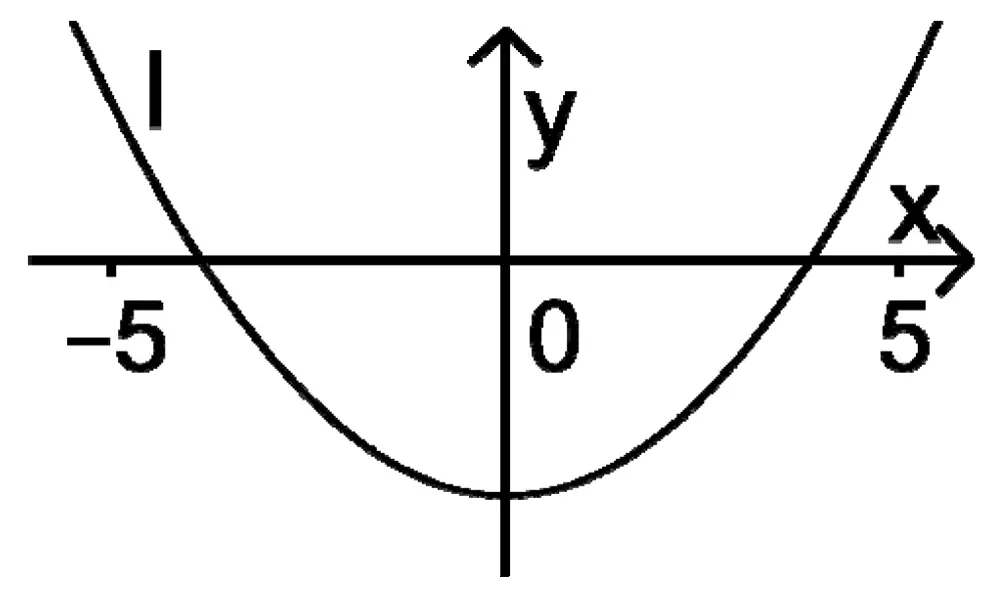
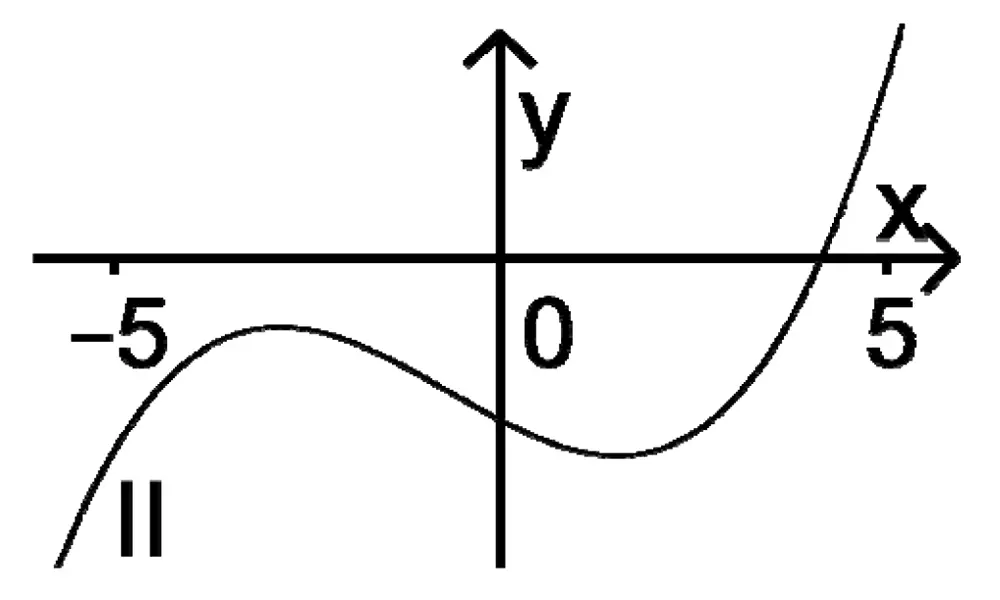
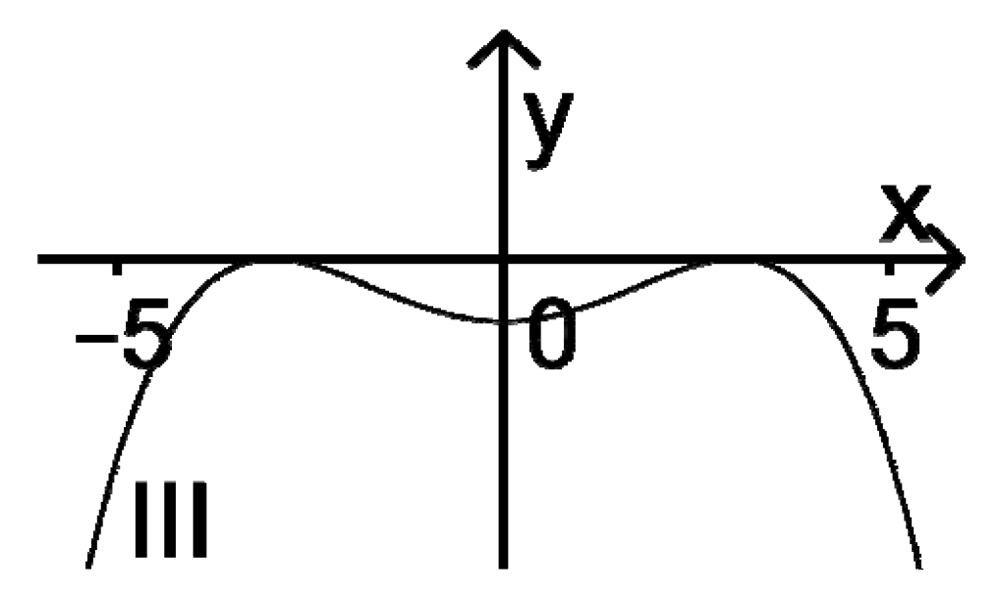
Der Graph einer in \(\mathbb R\) definierten Funktion \(g \, \colon \mapsto g(x)\) besitzt für \(-5 \leq x \leq 5\) zwei Wendepunkte. Entscheiden Sie, welcher der Graphen I, II und III zur zweiten Ableitungsfunktion \(g''\) von \(g\) gehört. Begründen Sie Ihre Entscheidung.
(2 BE)
Lösung zu Teilaufgabe 3
Graph I gehört zur zweiten Ableitungsfunktion \(g''\) von \(g\).
Anwendung der Differetialrechnung:
Wendepunkt
Ist \(f''(x_0) = 0\) und wechselt \(f''\) an der Stelle \(x_0\) das Vorzeichen, so hat \(G_f\) an der Stelle \(x_0\) einen Wendepunkt.
(vgl. Merkhilfe)
Alternative:
Es muss \(f''(x_{0}) = 0\) und \(f'''(x_{0}) \neq 0\) gelten.
Da der Graph der Funktion \(g\) für \(-5 \leq x \leq 5\) zwei Wendepunkte besitzt, muss der Graph der zweiten Ableitungsfunktion \(g''\) von \(g\) für \(-5 \leq x \leq 5\) zwei Nullstellen mit Vorzeichenwechsel besitzen. Somit kommt nur Graph I in Betracht.


