Auf der Kante \([AD]\) liegt der Punkt \(Q\), auf der Kante \([BE]\) der Punkt \(R(0|6|2)\). Das Dreieck \(FQR\) hat in \(Q\) einen rechten Winkel. Bestimmen Sie die \(x_3\)-Koordinate von \(Q\).
(5 BE)
Lösung zu Teilaufgabe f
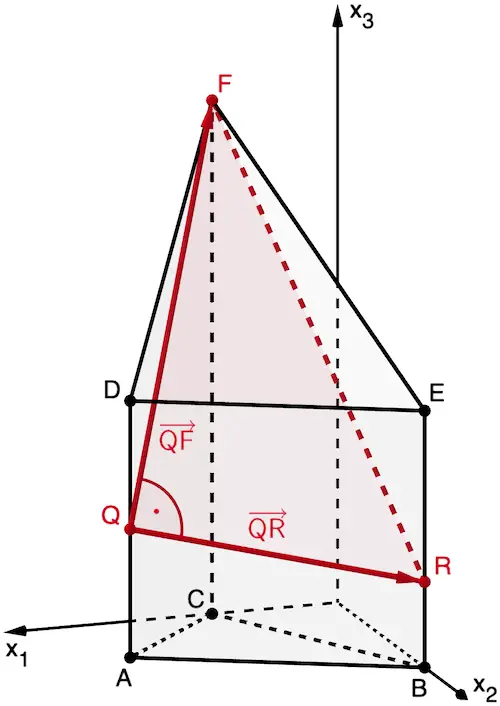
Planskizze (optional): Das Dreieck \(\textcolor{#cc071e}{FQR}\) hat bei \(\textcolor{#cc071e}{Q}\) einen rechten Winkel, wenn die Verbindungsvektoren \(\textcolor{#cc071e}{\overrightarrow{QR}}\) und \(\textcolor{#cc071e}{\overrightarrow{QF}}\) zueinander senkrecht sind. Dies ist dann der Fall, wenn das Skalarprodukt der Vektoren null ist.
Anwendung des Skalarprodukts:
Orthogonale (zueinander senkrechte) Vektoren (vgl. Merkhilfe)
\[\overrightarrow{a} \perp \overrightarrow{b} \; \Leftrightarrow \; \overrightarrow{a} \circ \overrightarrow{b} \quad (\overrightarrow{a} \neq \overrightarrow{0},\; \overrightarrow{b} \neq \overrightarrow{0})\]
\[\overrightarrow{QR} \perp \overrightarrow{QF}\;\Leftrightarrow \; \textcolor{#cc071e}{\overrightarrow{QR}} \circ \textcolor{#cc071e}{\overrightarrow{QF}} = \textcolor{#cc071e}{0}\]
Der Punkt \(Q\) liegt vertikal über Punkt \(A(6|3|0)\) auf der Kante \([AD]\) und hat somit dieselbe \(x_1\)- und \(x_2\)-Koordinate wie \(A\). Mit \(D(6|3|6)\) kann die \(x_3\)-Koordinate von \(Q\), im Folgenden mit \(q\) bezeichnet, nur Werte zwischen \(0\) und \(6\) annehmen.
\[\Rightarrow\;Q(6|3|q), \; q\in \;]0;6[\]
Verbindungsvektoren \(\textcolor{#cc071e}{\overrightarrow{QR}}\) und \(\textcolor{#cc071e}{\overrightarrow{QF}}\) bestimmen:
\(F(3|0|12)\), \(Q(6|3|q)\), \(R(0|6|2)\)
\[\textcolor{#cc071e}{\overrightarrow{QR}} = \overrightarrow{R} - \overrightarrow{Q} = \begin{pmatrix} 0\\6\\2 \end{pmatrix} - \begin{pmatrix} 6\\3\\q \end{pmatrix} = \textcolor{#cc071e}{\begin{pmatrix} -6 \\3\\2-q \end{pmatrix}}\]
\[\textcolor{#cc071e}{\overrightarrow{QF}} = \overrightarrow{F} - \overrightarrow{Q} = \begin{pmatrix} 3\\0\\12 \end{pmatrix} - \begin{pmatrix} 6\\3\\q \end{pmatrix} = \textcolor{#cc071e}{\begin{pmatrix} -3 \\-3\\12-q \end{pmatrix}}\]
Bedingung \(\textcolor{#cc071e}{\overrightarrow{QR}} \circ \textcolor{#cc071e}{\overrightarrow{QF}} = \textcolor{#cc071e}{0}\) ausformulieren:
Skalarprodukt
Unter dem Skalarprodukt \(\overrightarrow{a} \circ \overrightarrow{b}\) zweier Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) versteht man das Produkt aus den Beträgen der beiden Vektoren und dem Kosinus des von den Vektoren eingeschlossenen Winkels \(\varphi\).
\[\overrightarrow{a} \circ \overrightarrow{b} = \vert \overrightarrow{a} \vert \cdot \vert \overrightarrow{b} \vert \cdot \cos{\varphi} \quad (0^{\circ} \leq \varphi \leq 180^{\circ})\]
Berechnung eines Skalarprodukts im \(\boldsymbol{\mathbb R^{3}}\) (vgl. Merkhilfe)
\[\overrightarrow{a} \circ \overrightarrow{b} = \begin{pmatrix} a_{1} \\ a_{2} \\ a_{3} \end{pmatrix} \circ \begin{pmatrix} b_{1} \\ b_{2} \\ b_{3} \end{pmatrix} = a_{1}b_{1} + a_{2}b_{2} + a_{3}b_{3}\]
\[\begin{align*} \textcolor{#cc071e}{\overrightarrow{QR}} \circ \textcolor{#cc071e}{\overrightarrow{QF}} &= \textcolor{#cc071e}{0} \\[0.8em]\textcolor{#cc071e}{\begin{pmatrix} -6 \\3\\2-q \end{pmatrix}} \circ \textcolor{#cc071e}{\begin{pmatrix} -3 \\-3\\12-q \end{pmatrix}} &= \textcolor{#cc071e}{0} \\[0.8em] -6 \cdot (-3) + 3 \cdot (-3) + (2 - q) \cdot (12 - q) &= 0 \\[0.8em] 18 - 9 + 24 - 2q - 12q + q^2 &= 0 \\[0.8em] q^2 - 14q +33 &= 0 &&(q \in \;]0;6[)\end{align*}\]
Lösungsformel für quadratische Gleichungen (Mitternachtsformel) anwenden:
Lösungsformel für quadratische Gleichungen (vgl. Merkhilfe)
\[ax^2 + bx + c = 0 \,, \qquad a, b, c \in \mathbb R \,, \quad a \neq 0\]
\[\begin{align*} x_{1,2} &= \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}, \quad b^2 \geq 4ac \\[0.8em] x_{1,2} &= \frac{-b \pm \sqrt{D}}{2a}, \quad D \geq 0 \end{align*}\]
Diskriminante \(D = b^2 -4ac \;\):
\(D < 0\,\): keine Lösung
\(D = 0\,\): genau eine Lösung
\(D > 0\,\): zwei verschiedene Lösungen
\[q_{1,2} = \frac{14 \pm \sqrt{(-14)^2 - 4 \cdot 1 \cdot 33}}{2 \cdot 1} = \frac{14 \pm 8}{2} = 7 \pm 4\]
Mit \(q \in \;]0;6[\) kommt nur die Lösung \(q = 7 - 4 = 3\) infrage.
Die \(x_3\)-Koordinate von \(Q\) ist \(3\) und \(Q\) hat somit die Koordinaten \(Q(6|3|3)\).


