Der Hochpunkt des Graphen von \(f\) liegt auf einer Seite eines Quadrats; zwei Seiten dieses Quadrats liegen auf den Koordinatenachsen (vgl. Abbildung 1). Der Flächeninhalt des Quadrats stimmt mit dem Inhalt des Flächenstücks, das der Graph von \(f\) mit der \(x\)-Achse einschließt, überein. Bestimmen Sie den Wert von \(a\).
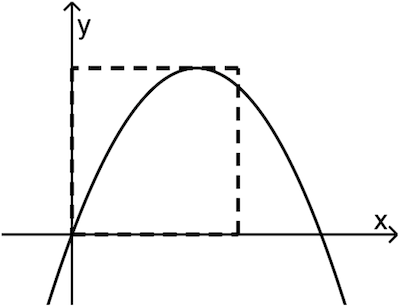Abb. 1
(3 BE)
Lösung zu Teilaufgabe 3b
Der Inhalt des Flächenstücks, das der Graph von \(f\) mit der \(x\)-Achse einschließt, ist aus Teilaufgabe a mit \(\dfrac{4}{3}a^3\) bekannt.
Der Hochpunkt des Graphen von \(f\) (Scheitelpunkt einer Parabel) liegt auf der Symmetrieachse mit der Gleichung \(x = a\) zwischen den bekannten Nullstellen \(x = 0\) und \(x = 2a\) (vgl. Angabe Aufgabe 3).
Also hat der Hochpunkt die Koordinaten \(\textcolor{#cc071e}{(a|f(a))}\) und damit ist \(\textcolor{#cc071e}{f(a)}\) die Seitenlänge des Quadrats.
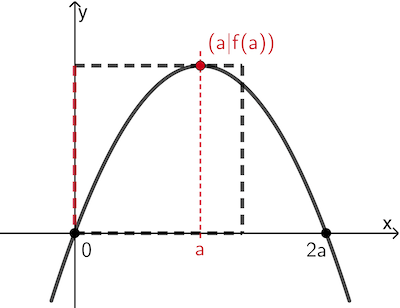Abb. 1
\(f(x) = -x^2 + 2ax\) (vgl. Angabe Aufgabe 3)
\[\textcolor{#cc071e}{f(a)} = -\textcolor{#cc071e}{a}^2 + 2a \cdot \textcolor{#cc071e}{a} = a^2\]
Somit folgt:
\[\begin{align*} \left[ \textcolor{#cc071e}{f(a)} \right]^2 &= \frac{4}{3}a^3 \\[0.8em] \left[ a^2 \right]^2 &= \frac{4}{3}a^3 \\[0.8em] a^4 &= \frac{4}{3}a^3 &&| \;-\frac{4}{3}a^3 \\[0.8em] a^4 - \frac{4}{3}a^3 &= 0 &&| \; a^3\;\text{ausklammern (Produkt formulieren)} \\[0.8em] a^3 \cdot \left( a - \frac{4}{3} \right) &= 0 &&| \; a \in \; ]1;+\infty[\;\text{(vgl. Angabe Aufgabe 3)} \\[0.8em] \Rightarrow a &= \frac{4}{3} \end{align*}\]
