Der Punkt \((2|3)\) ist der einzige Wendepunkt des Graphen von \(g\). Die in \(\mathbb R\) definierte Funktion \(h\) ist gegeben durch \(h(x) = g(2x) - 1\).
Geben Sie die Koordinaten des Wendepunkts des Graphen von \(h\) an und begründen Sie Ihre Angabe.
(3 BE)
Lösung zu Teilaufgabe 2b
\[h(x) = g(2x) - 1; \; D_h = \mathbb R\]
Wendepunkt des Graphen von \(h\): \((1|2)\)
Begründung
\[h(x) = g(\textcolor{#0087c1}{2}x)\textcolor{#cc071e}{-1}\]
Wie verändern die Parameter \(a\), \(b\), \(c\) und \(d\) den Graphen einer Funktion \(x \mapsto a \cdot f(b \cdot (x + c)) + d\) gegenüber dem Graphen einer Funktion \(x \mapsto f(x)\)?
Erst strecken oder spiegeln, dann verschieben!
Ein Vertauschen der Reihenfolge von Strecken und Verschieben bzw. Spiegel und Verschieben ergibt unterschiedliche Graphen und Funktionsterme.


Strecken in \(\boldsymbol{y}\)-Richtung mit dem Faktor \(\textcolor{#e9b509}{\boldsymbol{a}}\)
\(g(x) = \textcolor{#e9b509}{a} \cdot f(x)\) mit \(a \in \mathbb R\)
\(a < 0\) bewirkt zusätzlich eine Spiegelung an der \(x\)-Achse.

Strecken in \(\boldsymbol{x}\)-Richtung mit dem Faktor \(\textcolor{#e9b509}{\boldsymbol{\dfrac{1}{b}}}\)
\(h(x) = f(\textcolor{#e9b509}{b} \cdot x)\) mit \(b \in \mathbb R\)
\(b < 0\) bewirkt zusätzlich eine Spiegelung an der \(y\)-Achse.

Verschieben in \(\boldsymbol{y}\)-Richtung um \(\textcolor{#e9b509}{\boldsymbol{d}}\)
\(k(x) = f(x) + \textcolor{#e9b509}{d}\) mit \(d \in \mathbb R\)

Verschieben in \(\boldsymbol{x}\)-Richtung um \(\textcolor{#e9b509}{\boldsymbol{-c}}\)
\(l(x) = f(x + \textcolor{#e9b509}{c})\) mit \(c \in \mathbb R\)
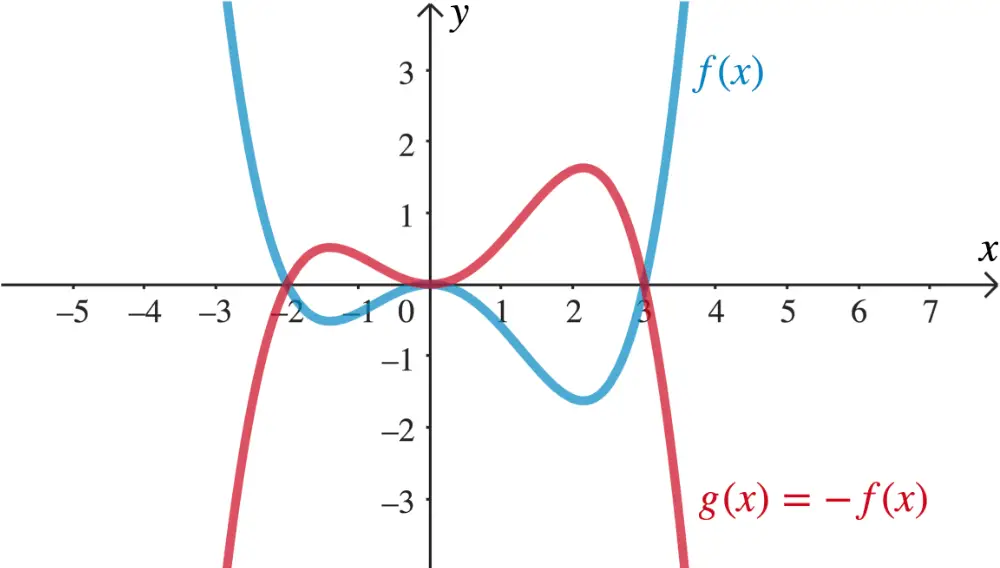
Spiegelung an der \(\boldsymbol{x}\)-Achse
\[g(x) = -f(x)\]

Spiegelung an der \(\boldsymbol{y}\)-Achse
\[h(x) = f(-x)\]
Der Graph der Funktion \(h\) geht aus dem Graphen der Funktion \(g\)
- durch Streckung in \(\textcolor{#0087c1}{x}\)-Richtung mit dem Faktor \(\textcolor{#0087c1}{\frac{1}{2}}\) und
- durch Verschiebung in \(\textcolor{#cc071e}{y}\)-Richtung um \(\textcolor{#cc071e}{-1}\)
hervor.
Wendepunkt des Graphen von \(g\): \((2|3)\)
Wendepunkt des Graphen von \(h\): \(\big(\textcolor{#0087c1}{\frac{1}{2}} \cdot 2|3 \textcolor{#cc071e}{-1}\big)\)
Somit ist der Punkt \((1|2)\) Wendepunkt des Graphen von \(h\).


