Gegeben ist die Funktion \(g \colon x \mapsto \sqrt{x-2}\) mit \(x \in [2;+\infty[\). Abbildung 2 zeigt den Graphen \(G\) von \(g\) sowie den Punkt \(P(3|1)\). Die Gerade mit der Gleichung \(y = \frac{1}{2}x-\frac{1}{2}\) ist Tangente an \(G\) im Punkt \(P\) und hat mit \(G\) nur den Punkt \(P\) gemeinsam.
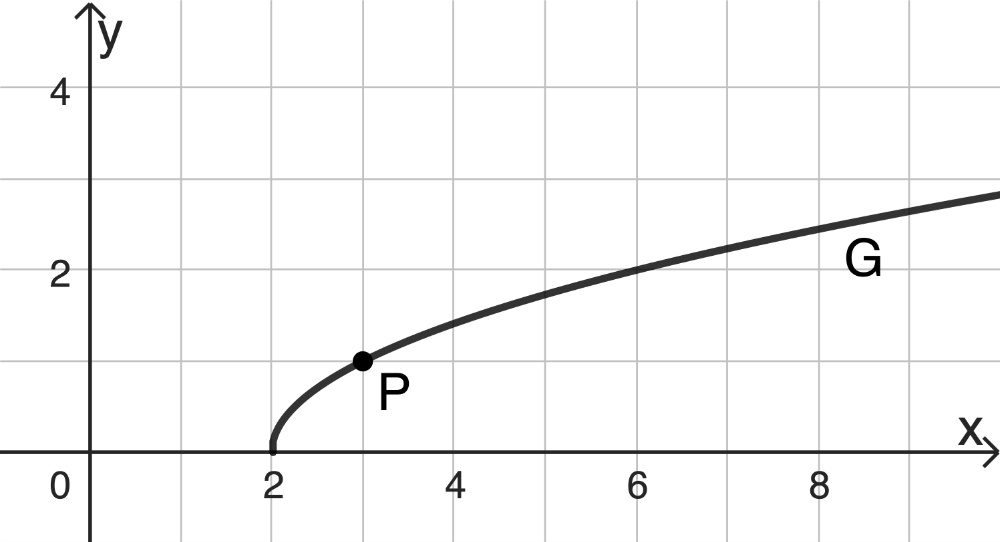 Abb. 2
Abb. 2
Zeichnen Sie die Tangente in Abbildung 2 ein.
(1 BE)
Lösung zu Teilaufgabe 4a

Tangente an den Graphen \(G\) im Punkt \(P(3|1)\)


