Machen Sie plausibel, dass das Volumen des Spats mithilfe der Formel \(V = G \cdot h\) berechnet werden kann, wobei \(G\) der Flächeninhalt des Rechtecks \(ABQP\) und \(h\) die zugehörige Höhe des Spats ist.
(3 BE)
Lösung zu Teilaufgabe e
Schrittweise Erläuterung
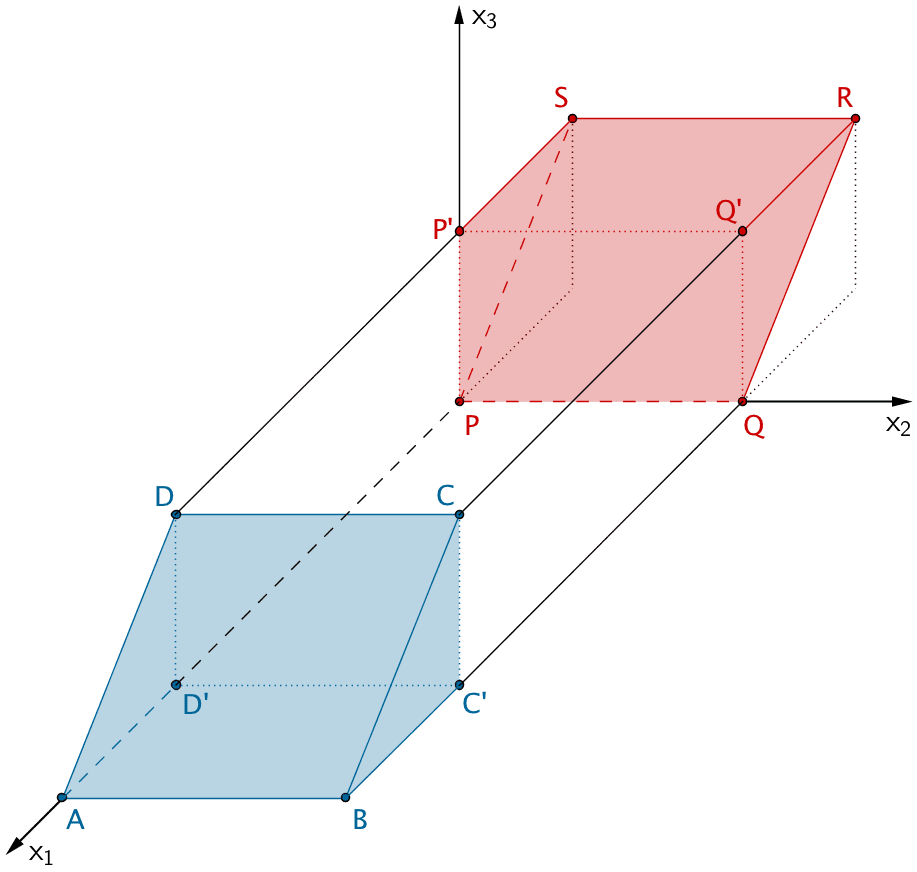
Teilt man den Spat einmal entlang der \(x_2x_3\)-Ebene und einmal entlang der parallelen Ebene, welche die Strecke \([DC]\) enthält, entstehen die beiden kongruenten Dreiecksprismen \(QRQ'PSP'\) und \(BCB'ADA'\).
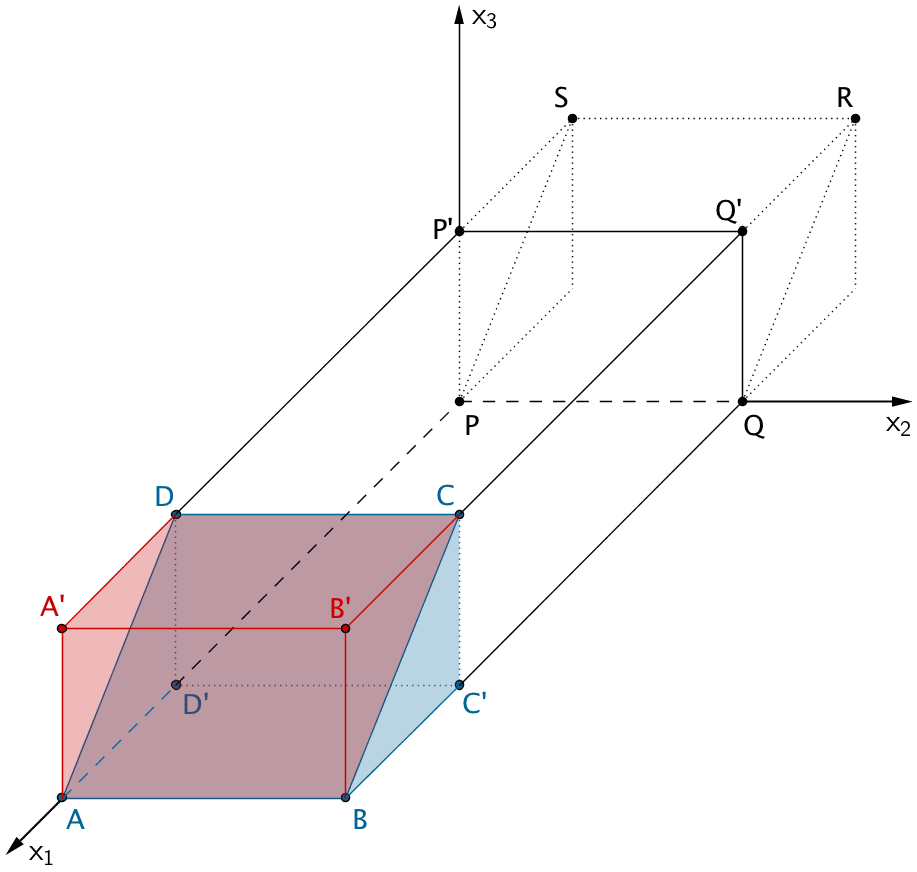
Verschiebt man das Dreiecksprisma \(QRQ'PSP'\) in Richtung der \(x_1\)-Achse, bis seine quadratische Seitenfläche \(PQRS\) mit der quadratischen Fläche \(ABCD\) des Spats zur Deckung kommt, entsteht der Quader \(ABQPA'B'Q'P'\), der den gleichen Volumeninhalt besitzt wie der Spat \(ABCDPQRS\).
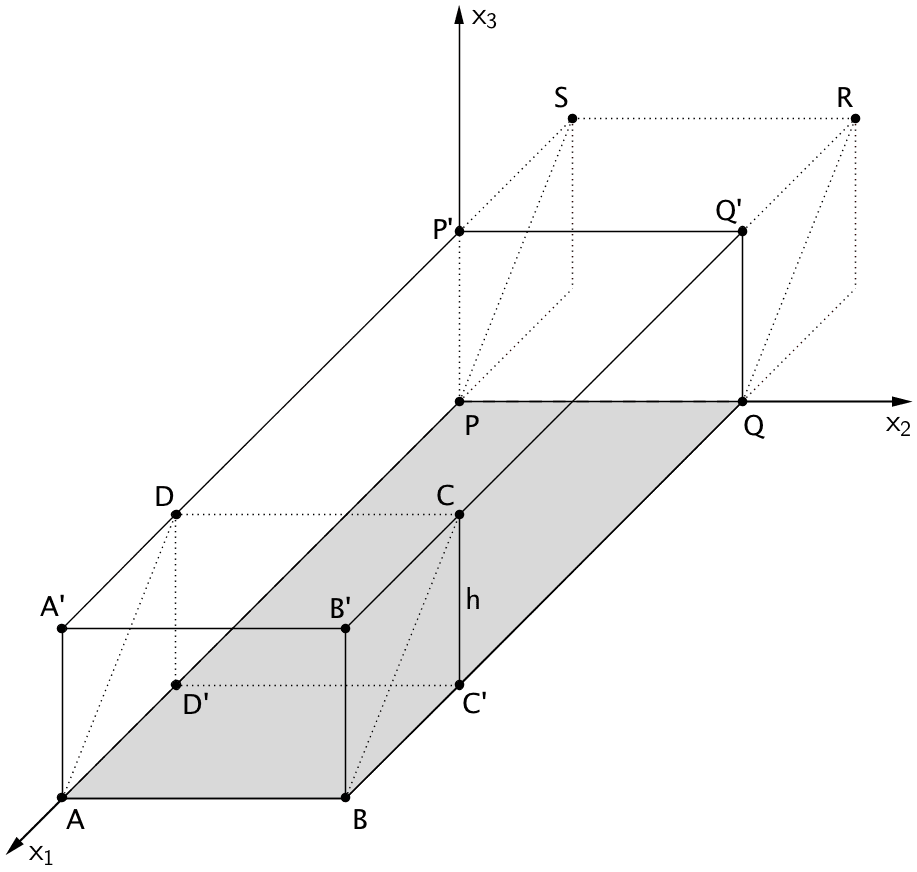
Für das Volumen des Quaders \(ABQPA'B'Q'P'\) gilt: \(V = G \cdot h\), wobei \(G\) der Flächeninhalt des Rechtecks \(ABQP\) und \(h\) die Höhe des Spats \(ABCDPQRS\) ist.


