Die Tangente an \(G_f\) im Punkt \(\big(\frac{9}{4}\big|0\big)\) wird mit \(t\) bezeichnet.
Weisen Sie nach, dass \(t\) durch den Punkt \(\big(0 \big| \frac{27}{8} \big)\) verläuft. Begründen Sie, dass der Inhalt des Flächenstücks, das \(G_f\) im ersten Quadranten mit \(t\) und der \(y\)-Achse einschließt, kleiner als \(\frac{1}{2} \cdot \frac{9}{4} \cdot \frac{27}{8}\) ist.
(5 BE)
Lösung zu Teilaufgabe 1c
Nachweis, dass \(t\) durch den Punkt \(\big(0\big| \frac{27}{8}\big)\) verläuft
Der Punkt \(\big( 0 \big|\frac{27}{8}\big)\) liegt auf der \(y\)-Achse. Es ist entweder zu zeigen, dass \(\frac{27}{8}\) der \(y\)-Achsenabschnitt der Tangente \(t\) ist, oder dass der Punkt \(\big(\frac{9}{4}\big|0\big)\) die Gleichung \(t \colon y = \textcolor{#cc071e}{m}x + \frac{27}{8}\) erfüllt. Vorab muss die Tangentensteigung \(\textcolor{#cc071e}{m}\) bestimmt werden.
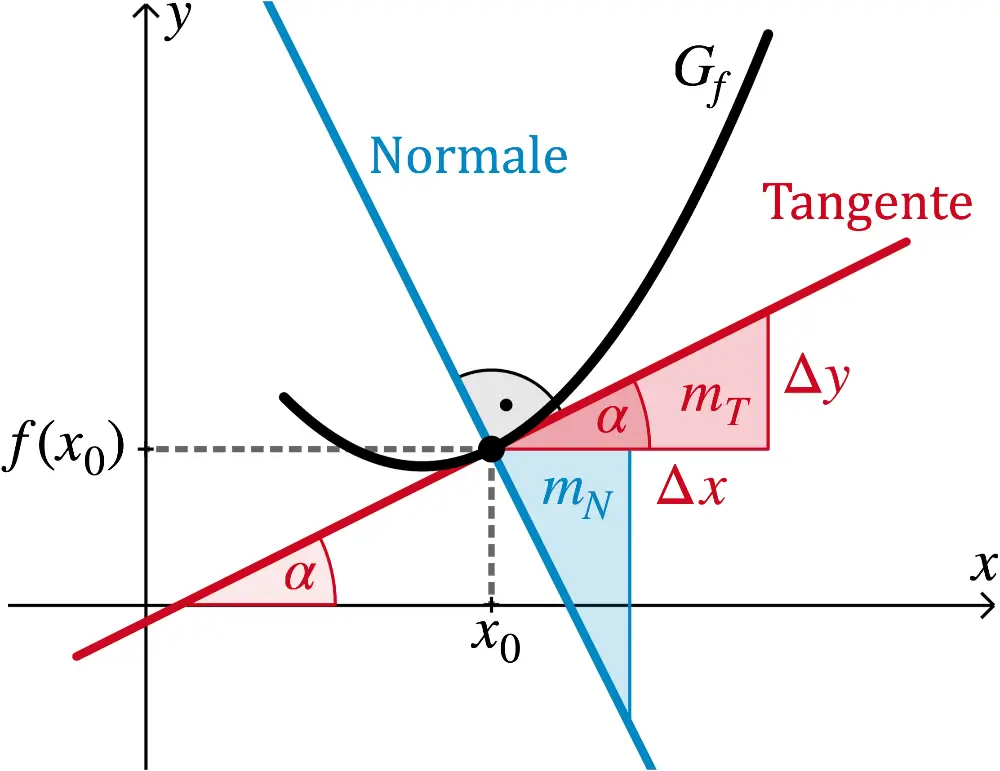
Tangentensteigung und Normalensteigung
\[\textcolor{#cc071e}{m_{T}} = f'(x_0) \qquad \textcolor{#0087c1}{m_{N}} = -\dfrac{1}{f'(x_0)}\]
Steigungswinkel \(\boldsymbol{\alpha}\) einer Tangente
\[{\textcolor{#cc071e}{\tan{\alpha}}} = f'(x_0)\]
\[\textcolor{#cc071e}{m} = f'\left(\frac{9}{4}\right) = -\frac{8}{9} \cdot \left( \frac{9}{4}\right)^2 + \frac{4}{3} \cdot \frac{9}{4} = \textcolor{#cc071e}{-\frac{3}{2}}\]
Ansatz: \(t \colon y = \textcolor{#cc071e}{-\dfrac{3}{2}}x + b\)
Koordinaten von Punkt \(\big(\textcolor{#e9b509}{\frac{9}{4}}\big|\textcolor{#e9b509}{0}\big)\) einsetzen und den \(y\)-Achsenabschnitt \(b\) bestimmen.
\[\begin{align*}\textcolor{#e9b509}{0} &= -\frac{3}{2} \cdot \textcolor{#e9b509}{\frac{9}{4}} + b \\[0.8em] 0 &= -\frac{27}{8} + b &&| +\frac{27}{8} \\[0.8em] \frac{27}{8} &= b\end{align*}\]
Ansatz: \(t \colon y = \textcolor{#cc071e}{-\dfrac{3}{2}}x + \dfrac{27}{8}\)
Koordinaten von Punkt \(\big(\textcolor{#e9b509}{\frac{9}{4}}\big|\textcolor{#e9b509}{0}\big)\) einsetzen und zeigen, dass sich eine wahre Aussage ergibt.
\[\begin{align*}\textcolor{#e9b509}{0} &= -\frac{3}{2} \cdot \textcolor{#e9b509}{\frac{9}{4}} + \frac{27}{8} \\[0.8em] 0 &= -\frac{27}{8} + \frac{27}{8} \\[0.8em] 0 &= 0\end{align*}\]
Also verläuft die Tangente \(t\) an \(G_f\) im Punkt \(\big(\frac{9}{4}\big|0\big)\) durch den Punkt \(\big( 0 \big|\frac{27}{8}\big)\).
Begründung, dass ...
... der Inhalt des Flächenstücks, das \(G_f\) im ersten Quadranten mit \(t\) und der \(y\)-Achse einschließt kleiner als \(\frac{1}{2} \cdot \frac{9}{4} \cdot \frac{27}{8}\) ist.
![Dreieck, das die Tangente t mit den Koordinatenachsen einschließt und Fläche, die der Graph von f im Intervall [0;9/4] mit der x-Achse einschließt sowie Fläche, die der Graph von f, die Tangente t und die y-Achse einschließen](/images/stories/BY2026BA_PT_B_B2/BY2026BA_PT_B_B2_1c_web.png)
Der Term \(\dfrac{1}{2} \cdot \textcolor{#0087c1}{\dfrac{9}{4}} \cdot \textcolor{#0087c1}{\dfrac{27}{8}}\) beschreibt den Flächeninhalt des Dreiecks, das die Tangente \(\textcolor{#cc071e}{t}\) mit den Koordinatenachsen einschließt.
Da \(G_f\) für \(0 < x < \frac{9}{4}\) im ersten Quadranten verläuft und somit innerhalb des Dreiecks, ist der Inhalt \(A\) des Flächenstücks, das \(G_f\) im ersten Quadranten mit der Tangente \(\textcolor{#cc071e}{t}\) und der \(y\)-Achse einschließt, kleiner als der Flächeninhalt des Dreiecks.
\[A = \frac{1}{2} \cdot \textcolor{#0087c1}{\frac{9}{4}} \cdot \textcolor{#0087c1}{\frac{27}{8}} - \textcolor{#e9b509}{\int_0^{\frac{9}{4}} f(x) dx}\]


