An einem Teil der südlichen Außenwand sind Solarmodule flächenbündig montiert. Die Solarmodule bedecken im Modell eine dreieckige Fläche, deren Eckpunkte die Spitze \(S\) sowie die Mittelpunkte der Kanten \([SB]\) und \([SC]\) sind.
Ermitteln Sie den Inhalt der von den Solarmodulen bedeckten Fläche.
(4 BE)
Lösung zu Teilaufgabe 1d
1. Lösungsansatz: Zweiter Strahlensatz
2. Lösungsansatz: Anwenden des Vektorprodunkts (Flächeninhalt eines Parallelogramms/Dreiecks)
3. Lösungsansatz: Trigonometrische Flächenberechnung
1. Lösungsansatz: Zweiter Strahlensatz
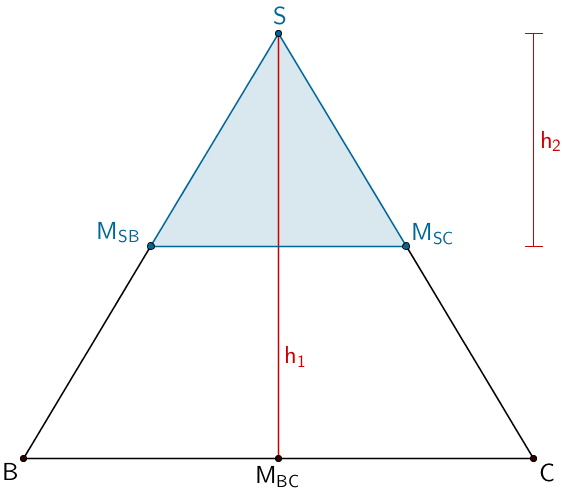
Dreieck \(BCS\) mit Höhe \(h_1\) und Dreieck \(M_{SB}M_{SC}S\) mit Höhe \(h_2\)
Flächeninhalt des Dreiecks \(M_{SB}M_{SC}S\):
\[A_{M_{SB}M_{SC}S} = \frac{1}{2} \cdot \overline{M_{SB}M_{SC}} \cdot h_2\]
Die Länge der Strecke \([M_{SB}M_{SC}]\) und die Länge der Höhe \(h_2\) lässt sich mithilfe des zweiten Strahlensatzes berechen.
Länge der Strecke \([M_{SB}M_{SC}]\) berechnen:
Strahlensätze (vgl. Merkhilfe)
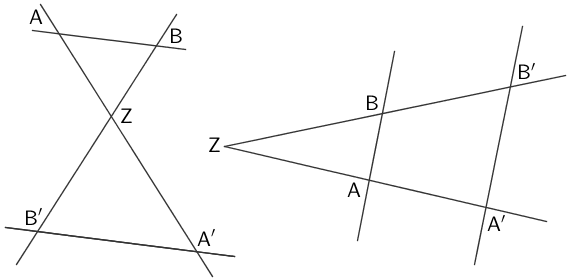
Erster Strahlensatz:
\[AB \parallel A'B' \quad \Longleftrightarrow \quad \frac{\overline{ZA}}{\overline{ZA'}} = \frac{\overline{ZB}}{\overline{ZB'}}\]
\[AB \parallel A'B' \quad \Longleftrightarrow \quad \frac{\overline{ZA}}{\overline{AA'}} = \frac{\overline{ZB}}{\overline{BB'}}\]
Zweiter Strahlensatz:
\[AB \parallel A'B' \quad \Longrightarrow \quad \frac{\overline{AB}}{\overline{A'B'}} = \frac{\overline{ZA}}{\overline{ZA'}}\]
\[\frac{\overline{SM_{SB}}}{\overline{SB}} = \frac{\overline{M_{SB}M_{SC}}}{\overline{BC}} = \frac{1}{2}\]
\[\Longrightarrow \quad \overline{M_{SB}M_{SC}} = \frac{1}{2} \cdot \overline{BC} = \frac{1}{2} \cdot 12 = 6\]
Länge der Höhe \(h_2\) berechnen:
Strahlensätze (vgl. Merkhilfe)
Erster Strahlensatz:
\[AB \parallel A'B' \quad \Longleftrightarrow \quad \frac{\overline{ZA}}{\overline{ZA'}} = \frac{\overline{ZB}}{\overline{ZB'}}\]
\[AB \parallel A'B' \quad \Longleftrightarrow \quad \frac{\overline{ZA}}{\overline{AA'}} = \frac{\overline{ZB}}{\overline{BB'}}\]
Zweiter Strahlensatz:
\[AB \parallel A'B' \quad \Longrightarrow \quad \frac{\overline{AB}}{\overline{A'B'}} = \frac{\overline{ZA}}{\overline{ZA'}}\]
\[\frac{h_2}{h_1} = \frac{\overline{M_{SB}M_{SC}}}{\overline{BC}} = \frac{6}{12} = \frac{1}{2}\]
\[\Longrightarrow \quad h_2 = \frac{1}{2} \cdot h_1\]
Länge der Höhe \(h_1\) berechnen:
![Mittelpunkte der Kanten [SB] und [SC], Mittelpunkt der Seitenlänge [BC], Höhe h₁ des Dreiecks BCS zur Grundlinie [BC]](/images/stories/B2013_G_II/B2013_G_II_1d.png "Mittelpunkte der Kanten [SB] und [SC], Mittelpunkt der Seitenlänge [BC], Höhe h₁ des Dreiecks BCS zur Grundlinie [BC]")
Im rechtwinkligen Dreieck \(SMM_{BC}\) gilt nach dem Satz des Pythagoras:
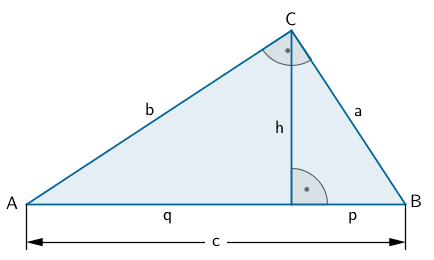
Satzgruppe des Pythagoras im rechtwinkligen Dreieck
Satz des Pythagoras
\[\hspace{5px}a^2 + b^2 = c^2\]
Höhensatz
\[h^2 = p \cdot q\]
Kathetensatz
\[a^2 = c \cdot p\,; \enspace b^2 = c \cdot q\]
\[\begin{align*} {h_1}^2 &= {\overline{MS}}^2 + {\overline{MM_{BC}}}^2 & &| \; \sqrt{\quad} \\[0.8em] h_1 &= \sqrt{{\overline{MS}}^2 + {\overline{MM_{BC}}}^2} \\[0.8em] &= \sqrt{8^2 + 6^2} \\[0.8em] &= 10 \end{align*}\]
\[\Longrightarrow \quad h_2 = \frac{1}{2} \cdot h_1 = \frac{1}{2} \cdot 10 = 5\]
Flächeninhalt \(A_{M_{SB}M_{SC}S}\) des Dreiecks \(M_{SB}M_{SC}S\) berechnen:
\[\begin{align*} A_{M_{SB}M_{SC}S} &= \frac{1}{2} \cdot \overline{M_{SB}M_{SC}} \cdot h_2 \\[0.8em] &= \frac{1}{2} \cdot 6 \cdot 5 \\[0.8em] &= 15 \end{align*}\]
Der Inhalt der von den Solarmodulen bedeckten Fläche beträgt 15 m².
2. Lösungsansatz: Anwenden des Vektorprodukts (Flächenihalt eines Parallelogramms/Dreiecks)
![Die Spitze S und die Mittelpunkte der Kanten [SB] und [SC] legen zwei linear unabhängige Vektoren fest, deren halbes Vektorprodukt gleich dem Inhalt der von den Solarmodulen bedeckten dreieckigen Fläche ist.](/images/stories/B2013_G_II/B2013_G_II_1d_03.png "Die Spitze S und die Mittelpunkte der Kanten [SB] und [SC] legen zwei linear unabhängige Vektoren fest, deren halbes Vektorprodukt gleich dem Inhalt der von den Solarmodulen bedeckten dreieckigen Fläche ist.")
Das halbe Vektorprodukt der Vektoren \(\overrightarrow{SM_{SB}}\) und \(\overrightarrow{SM_{SC}}\) ist gleich dem Inhalt der von den Solarmodulen bedeckten dreieckigen Fläche \(M_{SB}M_{SC}S\).
\[A_{M_{SB}M_{SC}S} = \frac{1}{2} \cdot \left| \left( \overrightarrow{SM_{SB}} \times \overrightarrow{SM_{SC}} \right) \right|\]
Anwendung des Vekorprodukts
Der Betrag des Vektorprodukts \(\overrightarrow{a} \times \overrightarrow{b}\) entspricht der Maßzahl des Flächeninhalts eines von zwei Vektoren \(\overrightarrow{a} \neq \overrightarrow{0}\) und \(\overrightarrow{b} \neq \overrightarrow{0}\) aufgespannten Parallelogramms.
\[\vert \overrightarrow{a} \times \overrightarrow{b} \vert = \vert \overrightarrow{a} \vert \cdot \textcolor{#cc071e}{\vert \overrightarrow{b} \vert \cdot \sin{\varphi}}\]
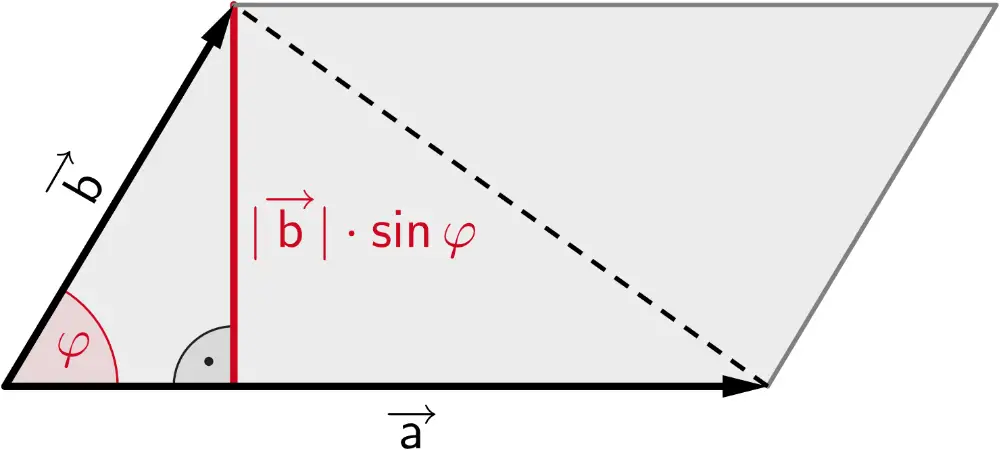
Flächeninhalt eines Parallelogramms
\[A = \vert \overrightarrow{a} \times \overrightarrow{b} \vert\]
Flächeninhalt eines Dreiecks
\[A = \frac{1}{2} \cdot \vert \overrightarrow{a} \times \overrightarrow{b} \vert\]
Vektoren \(\overrightarrow{SM_{SB}}\) und \(\overrightarrow{SM_{SC}}\) berechnen:
\[\begin{align*} \overrightarrow{SM_{SB}} &= \frac{1}{2} \cdot \overrightarrow{SB} \\[0.8em] &= \frac{1}{2} \cdot \left( \overrightarrow{B} - \overrightarrow{S} \right) \\[0.8em] &= \frac{1}{2} \cdot \left[ \begin{pmatrix} 12 \\ 12 \\ 0 \end{pmatrix} - \begin{pmatrix} 6 \\ 6 \\ 8 \end{pmatrix} \right] \\[0.8em] &= \begin{pmatrix} 3 \\ 3 \\ -4 \end{pmatrix} \end{align*}\]
\[\begin{align*} \overrightarrow{SM_{SC}} &= \frac{1}{2} \cdot \overrightarrow{SC} \\[0.8em] &= \frac{1}{2} \cdot \left( \overrightarrow{C} - \overrightarrow{S} \right) \\[0.8em] &= \frac{1}{2} \cdot \left[ \begin{pmatrix} 0 \\ 12 \\ 0 \end{pmatrix} - \begin{pmatrix} 6 \\ 6 \\ 8 \end{pmatrix} \right] \\[0.8em] &= \begin{pmatrix} -3 \\ 3 \\ -4 \end{pmatrix} \end{align*}\]
Flächeninhalt \(A_{M_{SB}M_{SC}S}\) des Dreiecks \(M_{SB}M_{SC}S\) berechnen:
Vektorprodukt (Kreuzprodukt)
Das Vektorprodukt \(\overrightarrow{a} \times \overrightarrow{b}\) zweier Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) erzeugt einen neuen Vektor \(\overrightarrow{c} = \overrightarrow{a} \times \overrightarrow{b}\) mit den Eigenschaften:
\(\overrightarrow{c}\) ist sowohl zu \(\overrightarrow{a}\) als auch zu \(\overrightarrow{b}\) senkrecht.
\[\overrightarrow{c} = \overrightarrow{a} \times \overrightarrow{b} \quad \Longrightarrow \quad \overrightarrow{c} \perp \overrightarrow{a}, \enspace \overrightarrow{c} \perp \overrightarrow{b}\]
Der Betrag des Vektorprodukts zweier Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) ist gleich dem Produkt aus den Beträgen der Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) und dem Sinus des von ihnen eingeschlossenen Winkels \(\varphi\).
\[\vert \overrightarrow{a} \times \overrightarrow{b} \vert = \vert \overrightarrow{a} \vert \cdot \vert \overrightarrow{b} \vert \cdot \sin{\varphi} \quad (0^{\circ} \leq \varphi \leq 180^{\circ})\]
Die Vektoren \(\overrightarrow{a}\), \(\overrightarrow{b}\) und \(\overrightarrow{c}\) bilden in dieser Reihenfolge ein Rechtssystem. Rechtehandregel: Weist \(\overrightarrow{a}\) in Richtung des Daumens und \(\overrightarrow{b}\) in Richtung des Zeigefingers, dann weist \(\overrightarrow{c} = \overrightarrow{a} \times \overrightarrow{b}\) in Richtung des Mittelfingers.
Berechnung eines Vektorprodukts im \(\boldsymbol{\mathbb R^{3}}\) (vgl. Merkhilfe)
\[\overrightarrow{a} \times \overrightarrow{b} = \begin {pmatrix} a_1 \\ a_2 \\ a_3 \end {pmatrix} \times \begin {pmatrix} b_1 \\ b_2 \\ b_3 \end {pmatrix} = \begin {pmatrix} a_2 \cdot b_3 - a_3 \cdot b_2 \\ a_3 \cdot b_1 - a_1 \cdot b_3 \\ a_1 \cdot b_2 - a_2 \cdot b_1 \end {pmatrix}\]
\[\begin{align*} A_{M_{SB}M_{SC}S} &= \frac{1}{2} \cdot \left| \left( \overrightarrow{SM_{SB}} \times \overrightarrow{SM_{SC}} \right) \right| \\[0.8em] &= \frac{1}{2} \cdot \left| \begin{pmatrix} 3 \\ 3 \\ -4 \end{pmatrix} \times \begin{pmatrix} -3 \\ 3 \\ -4 \end{pmatrix} \right| \\[0.8em] &= \frac{1}{2} \cdot \left| \begin{pmatrix} 3 & \cdot & (-4) & - & (-4) & \cdot & 3 \\ (-4) & \cdot & (-3) & - & 3 & \cdot & (-4) \\ 3 & \cdot & 3 & - & 3 & \cdot & (-3) \end{pmatrix} \right| \\[0.8em] &= \frac{1}{2} \cdot \left| \begin{pmatrix} 0 \\ 24 \\ 18 \end{pmatrix} \right| \\[0.8em] &= \frac{1}{2} \cdot \sqrt{0^2 + 24^2 + 18^2} \\[0.8em] &= \frac{1}{2} \cdot \sqrt{900} \\[0.8em] &= 15 \end{align*}\]
Der Inhalt der von den Solarmodulen bedeckten Fläche beträgt 15 m².
3. Lösungsansatz: Trigonometrische Flächenberechnung
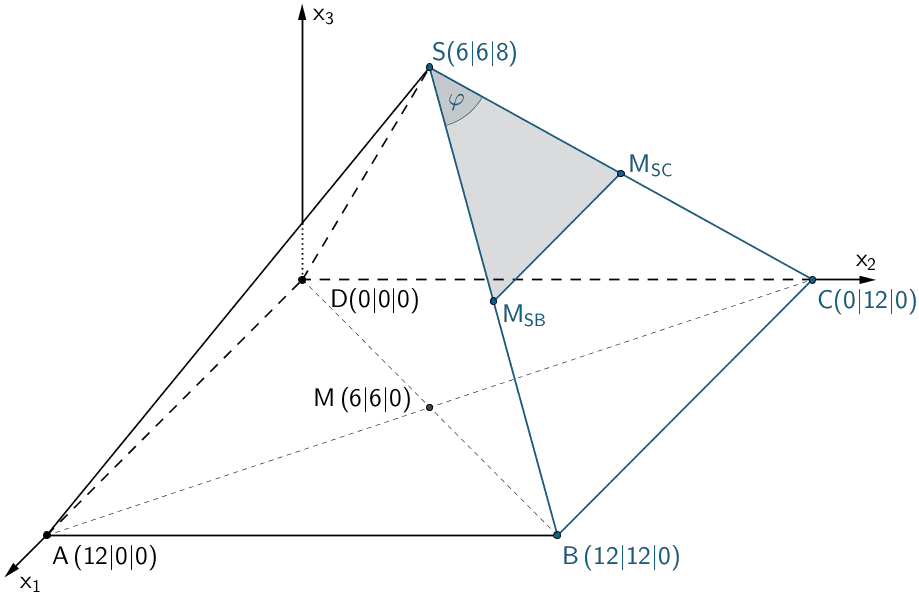
Ist z.B. das Maß \(\varphi\) des Winkels \(\measuredangle BSC\) bekannt, lässt sich der Flächeninhat \(A_{M_{SB}M_{SC}S}\) des Dreiecks \(M_{SB}M_{SC}S\) trigonometrisch berechnen.
Trigonometrische Berechnung im Allgemeinen Dreieck:
Flächeninhalt \(\boldsymbol{A}\) eines Dreiecks
\[A = \frac{1}{2} b \cdot c \cdot \sin \alpha\]
\[A = \frac{1}{2} a \cdot c \cdot \sin \beta\]
\[A = \frac{1}{2} a \cdot b \cdot \sin \gamma\]
\[\begin{align*}A_{M_{SB}M_{SC}S} &= \frac{1}{2} \cdot \overline{SM_{SB}} \cdot \overline{SM_{SC}} \cdot \sin{\varphi} & &| \; \overline{SM_{SB}} = \overline{SM_{SC}} \\[0.8em] &= \frac{1}{2} \cdot {\overline{SM_{SB}}}^2 \cdot \sin{\varphi} & &| \; \overline{SM_{SB}} = \frac{1}{2} \cdot \overline{SB} \\[0.8em] &= \frac{1}{8} \cdot {\overline{SB}}^2 \cdot \sin{\varphi} \end{align*}\]
Maß \(\varphi\) des Winkels \(\measuredangle BSC\) berechnen:
1. Möglichkeit: Winkel zwischen zwei Vektoren
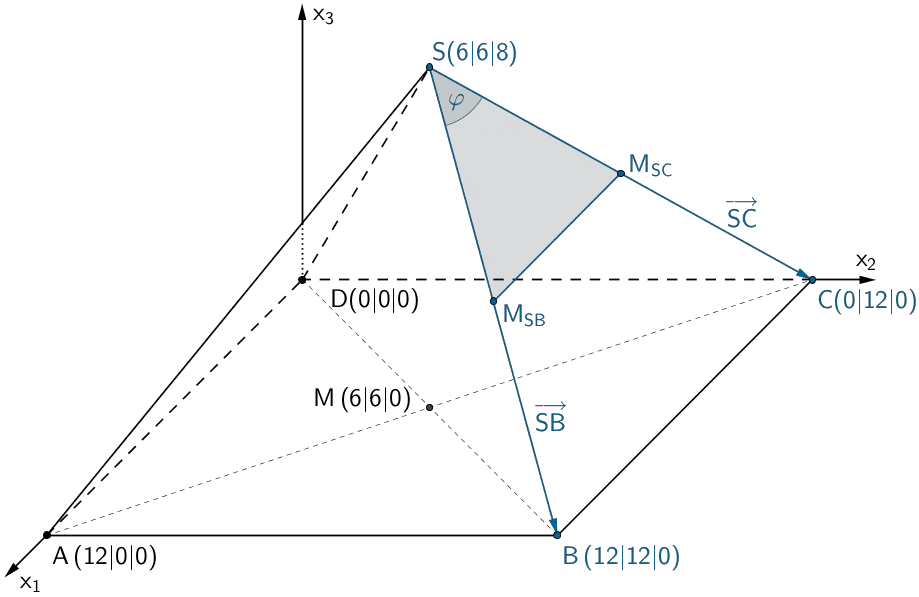
Maß \(\varphi\) des Winkels \(\measuredangle BSC\) zwischen den den Vektoren \(\overrightarrow{SB}\) und \(\overrightarrow{SC}\)
Anwendung des Skalarprodukts:
Winkel zwischen zwei Vektoren (vgl. Merkhilfe)
\[\cos \varphi = \frac{\overrightarrow{a} \circ \overrightarrow{b}}{\vert \overrightarrow{a} \vert \cdot \vert \overrightarrow{b} \vert}\,; \quad \varphi \in [0;\pi]\]
\[\begin{align*}\cos{\varphi} &= \frac{\vert \overrightarrow{SB} \circ \overrightarrow{SC} \vert}{\vert \overrightarrow{SB} \vert \cdot \vert \overrightarrow{SC} \vert} & &| \; \vert \overrightarrow{SB} \vert = \vert \overrightarrow{SC} \vert \\[0.8em] &= \frac{\vert \overrightarrow{SB} \circ \overrightarrow{SC} \vert}{{\vert \overrightarrow{SB} \vert}^2} \end{align*}\]
Vektoren \(\overrightarrow{SB}\) und \(\overrightarrow{SC}\) und deren Betrag berechnen:
\[\overrightarrow{SB} = \overrightarrow{B} - \overrightarrow{S} = \begin{pmatrix} 12 \\ 12 \\ 0 \end{pmatrix} - \begin{pmatrix} 6 \\ 6 \\ 8 \end{pmatrix} = \begin{pmatrix} 6 \\ 6 \\ -8 \end{pmatrix}\]
\[\overrightarrow{SC} = \overrightarrow{C} - \overrightarrow{S} = \begin{pmatrix} 0 \\ 12 \\ 0 \end{pmatrix} - \begin{pmatrix} 6 \\ 6 \\ 8 \end{pmatrix} = \begin{pmatrix} -6 \\ 6 \\ -8 \end{pmatrix}\]
\[\vert \overrightarrow{SB} \vert = \left| \begin{pmatrix} 6 \\ 6 \\ -8 \end{pmatrix} \right| = \sqrt{6^2 + 6^2 + (-8)^2} = 2\sqrt{34}\]
\[\begin{align*}\cos{\varphi} &= \frac{\vert \overrightarrow{SB} \circ \overrightarrow{SC} \vert}{{\vert \overrightarrow{SB} \vert}^2} \\[0.8em] &= \frac{\left| \begin{pmatrix} 6 \\ 6 \\ -8 \end{pmatrix} \circ \begin{pmatrix} -6 \\ 6 \\ -8 \end{pmatrix} \right|}{(2\sqrt{34})^2} \\[0.8em] &= \frac{\vert 6 \cdot (-6) + 6 \cdot 6 + (-8) \cdot (-8) \vert}{136} \\[0.8em] &= \frac{8}{17} & &| \; \cos^{-1}(\dots) \\[0.8em] \varphi &= 68{,}8^{\circ} \end{align*}\]
2. Möglichkeit: Satz des Pythagoras, Trigonometrie - rechtwinkliges Dreieck
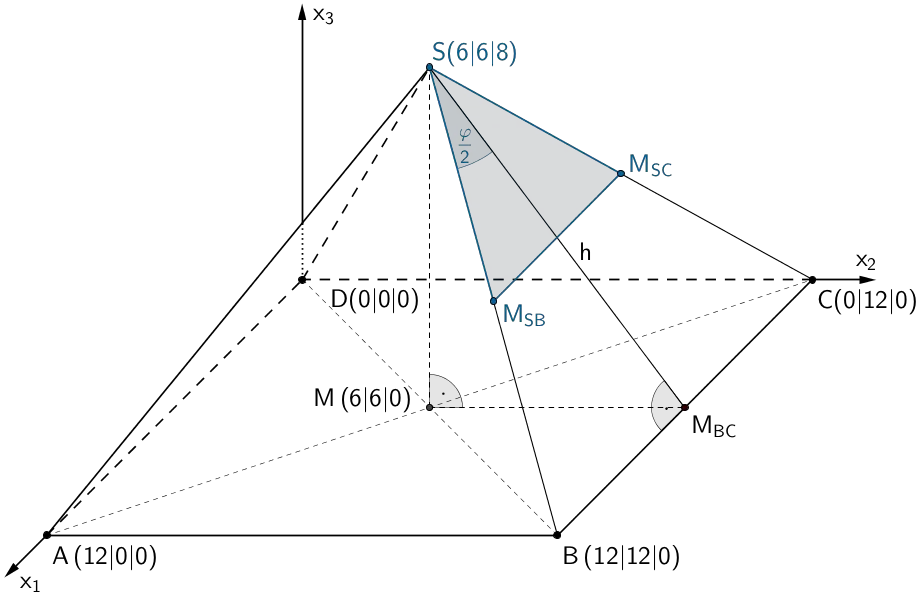
Höhe \(h\) des Dreiecks \(BCS\), rechtwinkliges Dreieck \(SMM_{BC}\) und rechtwinkliges Dreieck \(BM_{BC}S\)
Satz des Pythagoras im rechtwinkligen Dreieck \(SMM_{BC}\) anwenden:
Satzgruppe des Pythagoras im rechtwinkligen Dreieck
Satz des Pythagoras
\[\hspace{5px}a^2 + b^2 = c^2\]
Höhensatz
\[h^2 = p \cdot q\]
Kathetensatz
\[a^2 = c \cdot p\,; \enspace b^2 = c \cdot q\]
\[\begin{align*} {h}^2 &= {\overline{MS}}^2 + {\overline{MM_{BC}}}^2 & &| \; \sqrt{\quad} \\[0.8em] h &= \sqrt{{\overline{MS}}^2 + {\overline{MM_{BC}}}^2} \\[0.8em] &= \sqrt{8^2 + 6^2} \\[0.8em] &= 10 \end{align*}\]
Trigonometrische Beziehung im rechtwinkligen Dreieck \(BM_{BC}S\) anwenden:
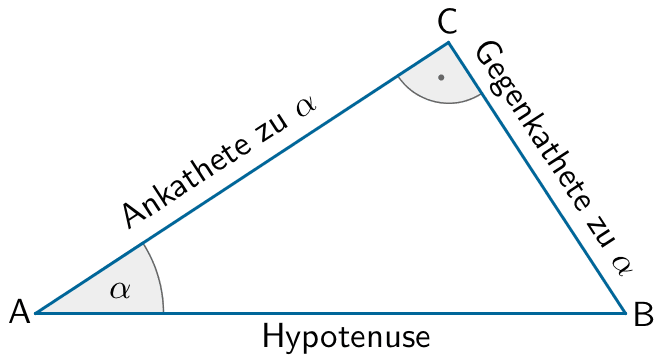
Trigonometrische Beziehungen im rechtwinkligen Dreieck (vgl. Merkhilfe)
\[\sin \alpha = \frac{\text{Gegenkathete}}{\text{Hypotenuse}}\]
\[\cos \alpha = \frac{\text{Ankathete}}{\text{Hypotenuse}}\]
\[\tan \alpha = \frac{\text{Gegenkathete}}{\text{Ankathete}}\]
\[\begin{align*}\tan{\frac{\varphi}{2}} &= \frac{\frac{1}{2} \cdot \overline{BC}}{h} \\[0.8em] &= \frac{6}{10} \\[0.8em] &= \frac{3}{5} & &| \; \tan^{-1}(\dots) \\[0.8em] \frac{\varphi}{2} &= 34{,}4^{\circ} & &| \cdot 2 \\[0.8em] \varphi &= 68{,}8^{\circ} \end{align*}\]
Flächeninhalt \(A_{M_{SB}M_{SC}S}\) des Dreiecks \(M_{SB}M_{SC}S\) berechnen:
\[\begin{align*}A_{M_{SB}M_{SC}S} &= \frac{1}{8} \cdot {\overline{SB}}^2 \cdot \sin{\varphi} \\[0.8em] &= \frac{1}{8} \cdot (2\sqrt{34})^2 \cdot \sin{68{,}8^{\circ}} \\[0.8em] &= 15 \end{align*}\]
Der Inhalt der von den Solarmodulen bedeckten Fläche beträgt 15 m².
