Eine auf einem Hausdach installierte Photovoltaikanlage wandelt Lichtenergie in elektrische Energie um. Für \(4 \leq x \leq 20\) beschreibt die Funktion \(p\) modellhaft die zeitliche Entwicklung der Leistung der Anlage an einem bestimmten Tag. Dabei ist \(x\) die seit Mitternacht vergangene Zeit in Stunden und \(p(x)\) die Leistung in kW (Kilowatt).
Bestimmen Sie rechnerisch die Uhrzeit am Nachmittag auf Minuten genau, ab der die Leistung der Anlage weniger als 40 % ihres Tageshöchstwerts von 10 kW beträgt.
(4 BE)
Lösung zu Teilaufgabe 3b
\(p(x) = \dfrac{40}{(x - 12)^{2} + 4}; \; 4 \leq x \leq 20\) (vgl. Angabe Aufgabe 3)
\(x\): Seit Mitternacht vergangene Zeit in Stunden (h)
\(p(x)\): Leistung in Kilowatt (kW)
\[\begin{align*} p(x) &= 0{,}4 \cdot 10 \\[0.8em] \frac{40}{(x - 12)^{2} + 4} &= 4 &&| \cdot [(x - 12)^{2} + 4] \\[0.8em] 40 &= 4 \cdot [(x - 12)^{2} + 4] &&| : 4 \\[0.8em] 10 &= (x - 12)^{2} + 4 &&| - 4 \\[0.8em] 6 &= (x - 12)^{2} &&| \; \sqrt{\quad} \\[0.8em] \pm \sqrt{6} &= x - 12 &&| + 12 \\[0.8em] 12 \pm \sqrt{6} &= x &&| \; 4 \leq x \leq 20 \\[0.8em] \Rightarrow \enspace x_{1}& = 12 + \sqrt{6} \approx 14{,}45 \\ (\textcolor{#cc071e}{x_{2}} &\textcolor{#cc071e}{=} \textcolor{#cc071e}{12 -\sqrt{6} \approx 9{,}55)} \end{align*}\]
Oder mithilfe der Lösungsformel für quadratische Gleichungen (Mitternachtsformel:
\[\begin{align*}p(x) &= 0{,}4 \cdot 10 \\[0.8em] &\enspace\vdots \\[0.8em] 6 &= (\textcolor{#e9b509}{x} - \textcolor{#0087c1}{12})^{2} &&| \; \text{2. B. F.:}\;(\textcolor{#e9b509}{a} - \textcolor{#0087c1}{b})^{2} = \textcolor{#e9b509}{a}^{2} - 2\textcolor{#e9b509}{a}\textcolor{#0087c1}{b} + \textcolor{#0087c1}{b}^{2} \\[0.8em] 6 &= x^{2} - 24x + 144 &&| - 6 \\[0.8em] 0 &= x^{2} - 24x + 138\end{align*}\]
Lösungsformel für quadratische Gleichungen (vgl. Merkhilfe)
\[ax^2 + bx + c = 0 \,, \qquad a, b, c \in \mathbb R \,, \quad a \neq 0\]
\[\begin{align*} x_{1,2} &= \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}, \quad b^2 \geq 4ac \\[0.8em] x_{1,2} &= \frac{-b \pm \sqrt{D}}{2a}, \quad D \geq 0 \end{align*}\]
Diskriminante \(D = b^2 -4ac \;\):
\(D < 0\,\): keine Lösung
\(D = 0\,\): genau eine Lösung
\(D > 0\,\): zwei verschiedene Lösungen
\[\begin{align*} x_{1,2} &= \frac{24 \pm \sqrt{(-24)^{2} - 4 \cdot 1 \cdot 138}}{2 \cdot 1} \\[0.8em] &= \frac{24 \pm \sqrt{24}}{2} \\[0.8em] &= \frac{24 \pm 2\sqrt{6}}{2} \\[0.8em] &= 12 \pm \sqrt{6} \\[0.8em] \Rightarrow \enspace x_{1}& = 12 + \sqrt{6} \approx 14{,}45 \\ (\textcolor{#cc071e}{x_{2}} &\textcolor{#cc071e}{=} \textcolor{#cc071e}{12 -\sqrt{6} \approx 9{,}55)}\end{align*}\]
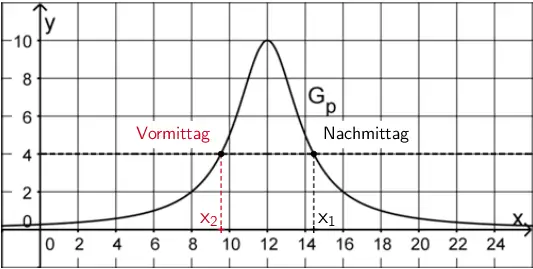
Die Lösung \(\textcolor{#cc071e}{x_{2} = 12 - \sqrt{6} \approx 9{,}55}\) kommt im Sachzusammenhang nicht in Betracht, da diese der Uhrzeit am Vormittag entspricht, zu der die Leistung erstmalig 40 % ihres Tageshöchstwerts von 10 kW erreicht.
Uhrzeit auf Minuten genau berechnen:
\[x_{1} \approx 14{,}45\; \text{h}\]
\[0{,}45\;\text{h} = 0{,}45 \cdot 60 \; \text{min} = 27\;\text{min}\]
Ab etwa 14:27 Uhr beträgt die Leistung der Anlage weniger als 40 % ihres Tageshöchstwerts von 10 kW.


