An der Stelle, die im Modell dem Punkt \(C\) entspricht, wird die Fahrlinie der Skifahrerin ohne Knick durch eine kreisbogenförmige Kurve fortgesetzt. Während der Fahrt entlang dieser Kurve erreicht die Skifahrerin eine Stelle, die dem Punkt \(D(18|-2|2)\) entspricht.
Der Kreisbogen, der diese Kurve beschreibt, ist Teil eines Kreises mit Mittelpunkt \(M(m_1|m_2|m_3)\). Die Koordinaten von \(M\) können mit folgendem Gleichungssystem ermittelt werden.
\[\textsf{I} \quad m_1 + m_2+2m_3 -20 = 0\]
\[\textsf{II} \;\begin{pmatrix} m_1 -9\\m_2 -1\\m_3 - 5 \end{pmatrix} \circ \begin{pmatrix}1{,}8\\0{,}2\\-1 \end{pmatrix} = 0\]
\[\textsf{III} \; \, \sqrt{(m_1-9)^2+(m_2-1)^2+(m_3-5)^2} = \sqrt{(m_1-18)^2+(m_2+2)^2+(m_3-2)^2}\]
Erläutern Sie die geometrischen Überlegungen, die den Gleichungen I, II und III zugrunde liegen.
(3 BE)
Lösung zu Teilaufgabe g
Gleichung \(\textsf{I}\): Der Mittelpunkt \(M\) liegt in der Ebenen \(E\).
Gleichung \(\textsf{II}\): Die Strecke \([MC]\) und die Gerade \(g_{0{,}8}\) sind zueinander senkrecht.
Gleichung \(\textsf{III}\): Die Punkte \(C\) und \(D\) haben vom Mittelpunkt \(M\) den gleichen Abstand.
Ausführliche Erklärung (nicht verlangt)
\[\textsf{I} \quad m_1 + m_2+2m_3 -20 = 0\]
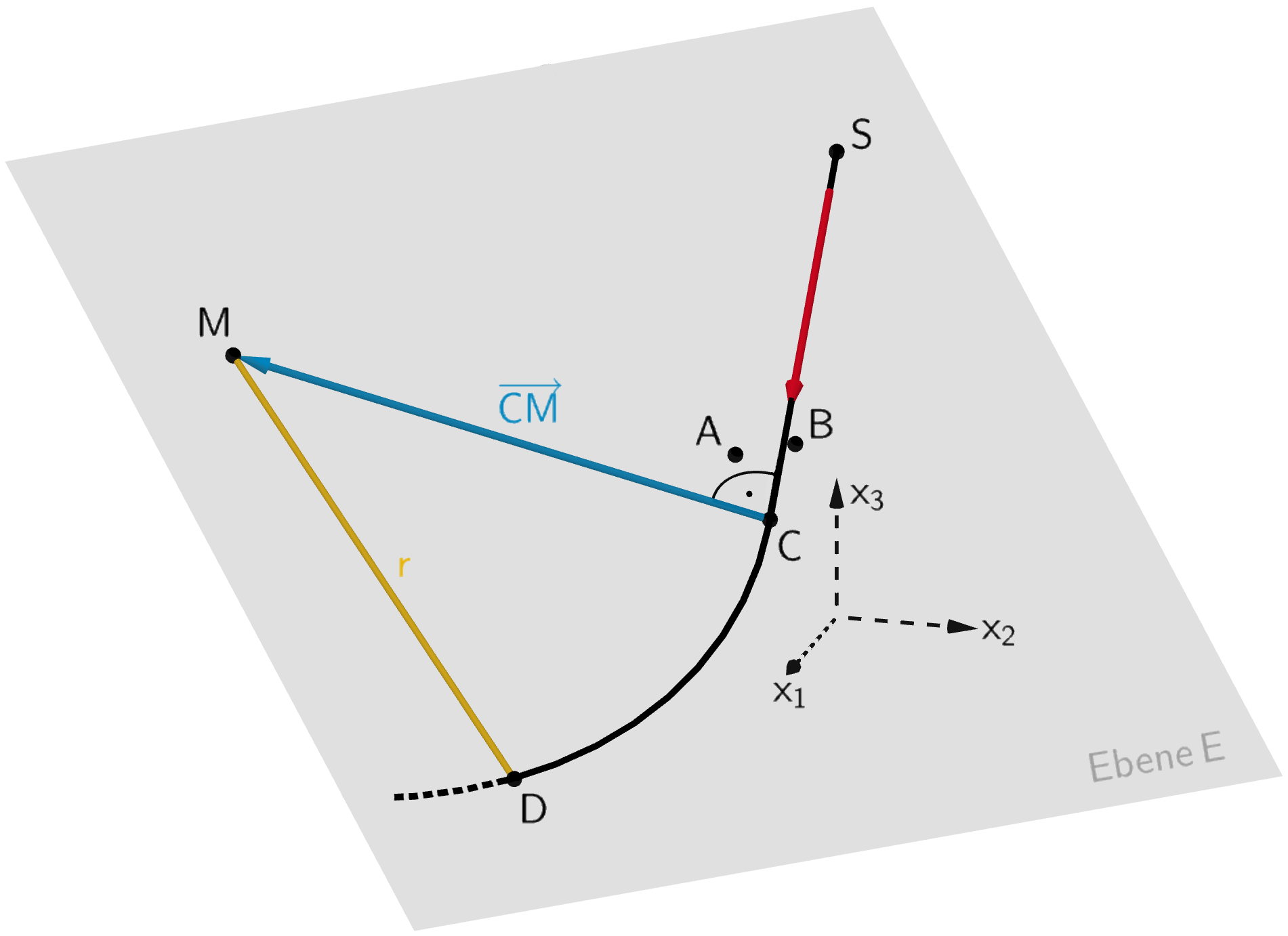
Damit der Kreisbogen \(\overset{\Large{\frown}}{DC}\) (Kurve) im Modell in der Ebene \(E\) liegt, muss dessen Mittelpunkt \(M\) in der Ebene \(E\) liegen.
Gleichung \(\textsf{I}\) formuliert diese Bedingung, indem die Koordinaten des Mittelpunkts \(M(m_1|m_2|m_3)\) in die Gleichung der Ebene \(E \colon x_1 +x_2+x_3 - 20 = 0\) eingesetzt sind.
\[\textsf{II} \enspace \, \textcolor{#0087c1}{\begin{pmatrix} m_1 -9\\m_2 -1\\m_3 - 5 \end{pmatrix}} \circ \textcolor{#cc071e}{\begin{pmatrix}1{,}8\\0{,}2\\-1\end{pmatrix}} = 0\]
Damit der Kreisbogen \(\overset{\Large{\frown}}{DC}\) (Kurve) im Modell ohne Knick an die Gerade \(g_{0{,}8}\) (gerade Fahrlinie) anschließt, müssen die Strecke \([MC]\) und die Gerade \(g_{0{,}8}\) zueinander senkrecht sein. Dies ist dann der Fall, wenn das Skalarprodukt aus dem Richtungsvektor der Gerade \(g_{0{,}8} \colon \overrightarrow{X} = \begin{pmatrix} 0\\0\\10 \end{pmatrix} + \lambda \cdot \textcolor{#cc071e}{\begin{pmatrix} 1{,}8\\0{,}2\\-1 \end{pmatrix}}\) und dem Vektor \(\textcolor{#0087c1}{\overrightarrow{CM}} = \textcolor{#0087c1}{\begin{pmatrix} m_1 -9\\m_2 -1\\m_3 - 5 \end{pmatrix}}\) gleich null ist. Gleichung \(\textsf{II}\) beschreibt diese Bedingung.
Anwendung des Skalarprodukts:
Orthogonale (zueinander senkrechte) Vektoren (vgl. Merkhilfe)
\[\overrightarrow{a} \perp \overrightarrow{b} \; \Leftrightarrow \; \overrightarrow{a} \circ \overrightarrow{b} \quad (\overrightarrow{a} \neq \overrightarrow{0},\; \overrightarrow{b} \neq \overrightarrow{0})\]
\[\textsf{III} \quad \underbrace{\sqrt{(m_1-9)^2+(m_2-1)^2+(m_3-5)^2}}_{\Large{\textcolor{#0087c1}{r}\,=\,d(M;C)}} = \underbrace{\sqrt{(m_1-18)^2+(m_2+2)^2+(m_3-2)^2}}_{\Large{\textcolor{#e9b509}{r}\,=\,d(M;D)}}\]
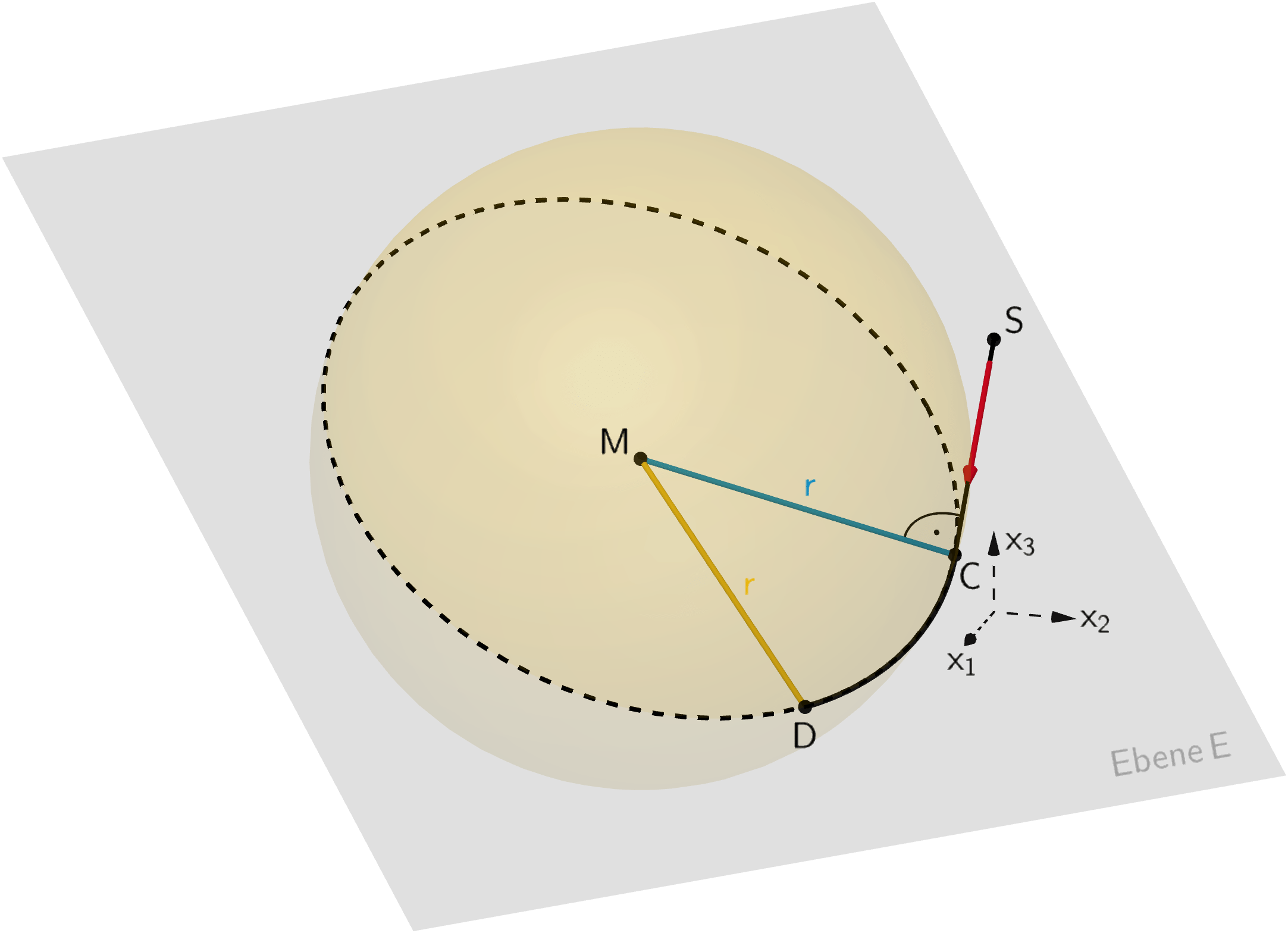
Der Kreisbogen \(\overset{\Large{\frown}}{DC}\) mit \(C(9|1|5)\) und \(D(18|-2|2)\) (vgl. Angabe) ist Teil des Schnittkreises, den die Kugel mit Mittelpunkt \(M\) und Radius \(r = d(M;D) = d(M;C)\) mit der Ebene \(E\) bildet.
Kugelgleichung
Eine Kugel mit dem Mittelpunkt \(M(m_{1}|m_{2}|m_{3})\) und dem Radius \(r\) wird beschrieben durch:
Vektordarstellung
\[(\overrightarrow{X} - \overrightarrow{M})^{2} = r^{2}\]
Koordinatendarstellung
\[(x_{1} - m_{1})^{2} + (x_{2} - m_{2})^{2} + (x_{3} - m_{3})^{2} = r^{2}\]
Gleichung \(\textsf{III}\) formuliert ausgehend von der Kugelgleichung \((m_1 - x_1)^2 + (m_2 - x_2)^2 + (m_3 - x_3)^2 = r^2\) die Bedingung \(r = d(M;D) = d(M;C)\). Das heiß, die Punkte \(C\) und \(D\) müssen vom Mittelpunkt \(M\) den gleichen Abstand haben.


