Berechnen Sie die Funktionswerte \(p(0)\), \(p(\pi)\), \(p(2\pi)\), \(p(3\pi)\) und \(p(4\pi)\). Zeichnen Sie für \(x \geq 0\) den Graphen von \(p\) sowie den Graphen der in \(\mathbb R\) definierten Funktion \(-p\,\colon x \mapsto -p(x)\) unter Berücksichtigung der bisherigen Ereignisse in die Abbildung ein.
(4 BE)
Lösung zu Teilaufgabe 2b
\[p(x) = e^{-\frac{1}{4}x}\,; \quad D = \mathbb R\]
Berechnung der Funktionswerte \(p(0)\), \(p(\pi)\), \(p(2\pi)\), \(p(3\pi)\) und \(p(4\pi)\)
\[p(0) = e^{-\frac{1}{4} \cdot 0} = 1\]
\[p(\pi) = e^{-\frac{1}{4} \cdot \pi} \approx 0{,}46\]
\[p(2\pi) = e^{-\frac{1}{4} \cdot 2\pi} \approx 0{,}21\]
\[p(3\pi) = e^{-\frac{1}{4} \cdot 3\pi} \approx 0{,}09\]
\[p(4\pi) = e^{-\frac{1}{4} \cdot 4\pi} \approx 0{,}04\]
Zeichnung des Graphen von \(p\) sowie des Graphen von \(-p\) für \(x \geq 0\)
Bisherige Ergebnisse (siehe Teilaufgabe 2a):
- Der Graph von \(p\) ist für alle \(x \in \mathbb R\) streng monoton fallend.
- \[\lim \limits_{x \to +\infty} p(x) = 0\]
- \[\lim \limits_{x \to -\infty} p(x) = +\infty\]
Der Graph der Funktion \(-p\) entsteht durch Spiegelung des Graphen der Funktion \(p\) an der \(x\)-Achse.
Spiegeln von Funktionsgraphen
Spiegelung an der \(x\)-Achse: \(g(x) = -f(x)\)
Spiegelung an der \(y\)-Achse: \(h(x) = f(-x)\)
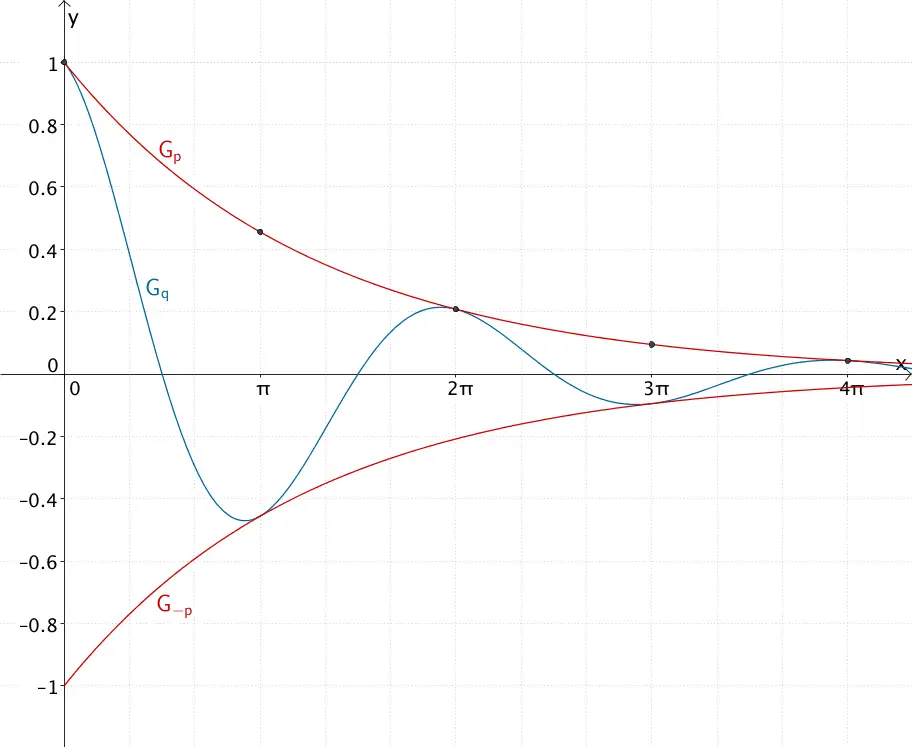
Graph der Funktion \(p\) und Graph der Funktion \(-p\), Graph der Funktion \(g\)

