Die Anzahl der KInder, die eine Frau im Laufe ihres Lebens durchschnittlich zur Welt bringt, wird durch eine sogenannte Geburtenziffer angegeben, die jedes Jahr statistisch ermittelt wird.

Die Funktion \(g_{1{,}4} \colon x \mapsto 2x \cdot e^{-0{,}5x^2} + 1{,}4\) beschreibt für \(x \geq 0\) modelhaft die zeitliche Entwicklung der Geburtenziffer in einem europäischen Land. Dabei ist \(x\) die seit dem Jahr 1955 vergangene Zeit in Jahrzehnten (d.h. \(x = 1\) entspricht dem Jahr 1965) und \(g_{1{,}4} (x)\) die Geburtenziffer. Damit die Bevölkerungszahl in diesem Land langfristig näherungsweise konstant bleibt, ist dort eine Geburtenziffer von etwa 2,1 erforderlich.

Zeichnen Sie den Graphen von \(g_{1{,}4}\) in Abbildung 2 ein und ermitteln Sie graphisch mit angemessener Genauigkeit, in welchem Zeitraum die Geburtenziffer mindestens 2,1 beträgt.

(4 BE)

Lösung zu Teilaufgabe 3a

\[g_{1{,}4}(x) = 2x \cdot e^{-0{,}5x^2} + 1{,}4\,; \quad x \geq 0\]

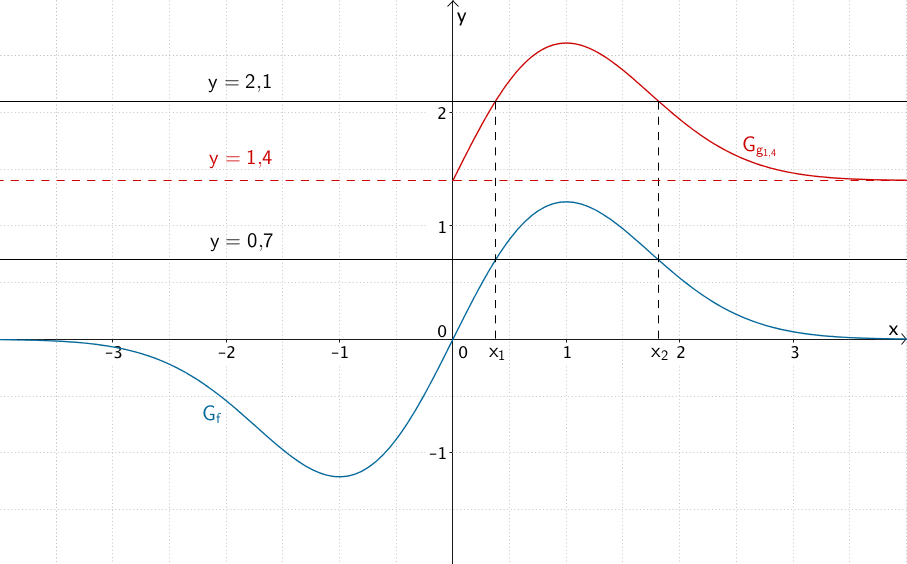
Im Rahmen der Ablesegenauigkeit entnimmt man die \(x\)-Koordinaten der Schnittpunkte des Graphen von \(g_{1{,}4}\) und der Geraden \(y = 2{,}1\).

\[x_1 \approx 0{,}4\,; \quad x_2 \approx 1{,}8\]

\(x_1 \approx 0{,}4\) entspricht dem Jahr 1959.

\(x_2 \approx 1{,}8\) entspricht dem Jahr 1973.

Im Zeitraum von 1959 bis 1973 beträgt die Geburtenziffer mindestens 2,1.

Anmerkung: Der gesuchte Zeitraum lässt sich ebenfalls am u.U. genaueren Graphen der Funktion \(f\) ablesen. In diesem Fall muss \(f(x) = 2{,}1 - 1{,}4 = 0{,}7\) gelten. Man liest also die \(x\)-Koordinaten der Schnittpunkte des Graphen von \(f\) und der Geraden \(y = 0{,}7\) ab.