Die Schülerinnen und Schüler untersuchen nun den Abstand \(d(x)\) der Graphenpunkte \(P_{x}(x|p(x))\) vom Ursprung des Koordinatensystems.
Zeigen Sie, dass \(d(x) = \sqrt{0{,}04x^{4} - x^{2} + 25}\) gilt.
(3 BE)
Lösung zu Teilaufgabe 1b
Satz des Pythagoras anwenden
\[d(x) = \sqrt{0{,}04x^{4} - x^{2} + 25}\]
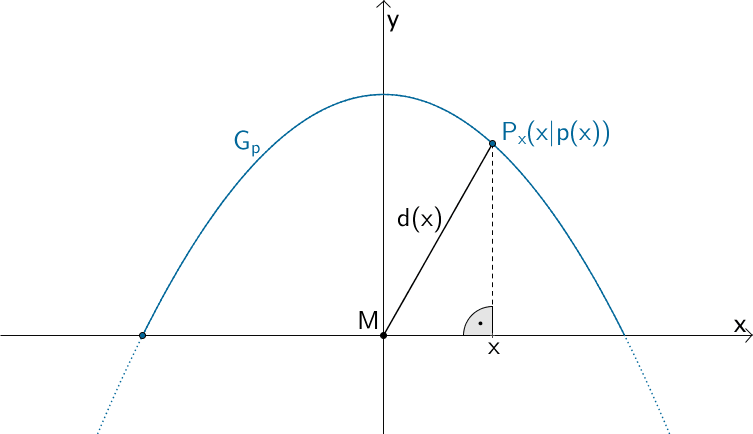
Der Abstand \(d(x)\) der Graphenpunkte \(P_{x}(x|p(x))\) vom Ursprung des Koordinatensystems \((M)\) lässt sich mithilfe des Satzes des Pythagoras beschreiben.
Satz des Pythagoras anwenden:
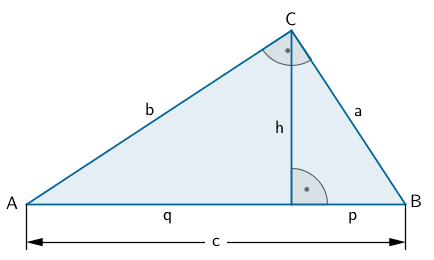
Satzgruppe des Pythagoras im rechtwinkligen Dreieck
Satz des Pythagoras
\[\hspace{5px}a^2 + b^2 = c^2\]
Höhensatz
\[h^2 = p \cdot q\]
Kathetensatz
\[a^2 = c \cdot p\,; \enspace b^2 = c \cdot q\]
\[p(x) = -0{,}2x^{2} + 5; \; D_{p} = [-5;5]\]
\[\begin{align*} [d(x)]^{2} &= x^{2} + [p(x)]^{2} & &| \; \sqrt{\enspace} \enspace (d(x) > 0) \\[0.8em] d(x) &= \sqrt{x^{2} + [p(x)]^{2}} \\[0.8em] &= \sqrt{x^{2} + (-0{,}2x^{2} + 5)^{2}} \\[0.8em] &= \sqrt{x^{2} + 0{,}04x^{4} - 2x^{2} + 25} \\[0.8em] &= \sqrt{0{,}04x^{2} - x^{2} + 25} \end{align*}\]
Anmerkung:
Der Abstand d(x) der Graphenpunkte \(P_{x}(x|p(x))\) vom Koordinatenursprung ist ein im Sachzusammenhang positiver Wert. Wegen \(d(x) > 0\) kann hier die Wurzel beidseitig der Gleichung „problemlos" (ohne Fallunterscheidung) gezogen werden. Das ist nicht selbstverständlich, denn allgemein gilt: \(\sqrt{a^{2}} = \vert a \vert; \; a \in \mathbb R\).


