In einem Koordinatensystem (vgl. Abbildung 1) werden alle Rechtecke betrachtet, die folgende Bedingungen erfüllen:
-
Zwei Seiten liegen auf den Koordinatenachsen.
-
Ein Eckpunkt liegt auf dem Graphen \(G_f\) der Funktion \(f \, \colon x \mapsto -\ln x\) mit \(0 < x < 1\).
Abbildung 1 zeigt ein solches Rechteck.
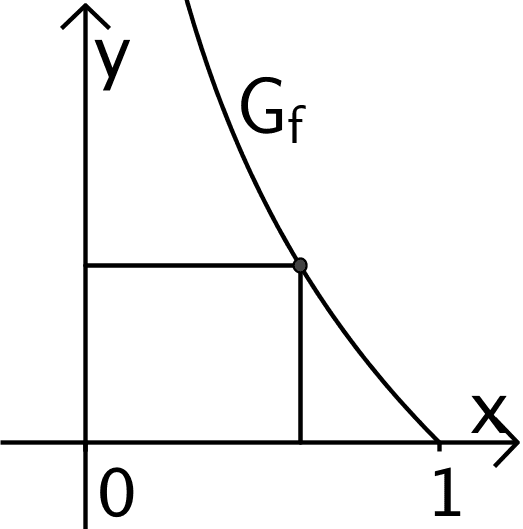 Abb. 1
Abb. 1
Unter den betrachteten Rechtecken gibt es eines mit größtem Flächeninhalt. Berechnen Sie die Seitenlängen dieses Rechtecks.
(5 BE)
Lösung zu Teilaufgabe 4
\[f(x) = -\ln x \,; \quad 0 < x < 1\]
Flächeninhalt \(A\) der Rechtecke in Abhängigkeit von \(x\) bestimmen:
\[\begin{align*} A(x) &= x \cdot f(x) \\[0.8em] &= x \cdot (-\ln x) \\[0.8em] &= - x \cdot \ln x \end{align*}\]
Notwendige Bedingung für maximalen Flächeninhalt:
\[A'(x) \overset{!}{=} 0\]
Erste Ableitung \(A'\) bilden:
\[A(x) = - x \cdot \ln x\]
Produktregel
\[f(x) = u(x) \cdot v(x) \quad \Longrightarrow \quad f'(x) = u'(x) \cdot v(x) + u(x) \cdot v'(x)\]
Ableitung einer Potenzfunktion
\[f(x) = x^r \quad \Longrightarrow \quad f'(x) = rx^{r - 1} \quad (r \in \mathbb R)\]
Ableitung der natürlichen Logarithmusfunktion:
\[f(x) = \ln x \quad (x > 0) \quad \Longrightarrow \quad f'(x) = \frac{1}{x}\]
(vgl. Merkhilfe)
\[\begin{align*}A'(x) &= - 1 \cdot \ln x + (-x) \cdot \frac{1}{x} \\[0.8em] &= -\ln x - 1 \end{align*}\]
\[\begin{align*} A'(x) \overset{!}{=} 0 \quad \Longrightarrow \quad -\ln x - 1 &= 0 & &| + \ln{x} \\[0.8em] -1 &= \ln{x} & &| \; a^x = b \enspace \Longleftrightarrow \enspace x = \log_{a}{b} \\[0.8em] e^{-1} &= x \\[0.8em] \frac{1}{e} &= x \end{align*}\]
\(\Longrightarrow \quad\) Für \(\displaystyle x = \frac{1}{e}\) ist der Flächeninhalt \(A\) des Rechtecks extremal.
Art des Extremums nachweisen:
Anwendung der Differentialrechnung:
Art von Extrempunkten mithilfe der zweiten Ableitung nachweisen
Ist \(f'(x_{0}) = 0\) und \(f''(x_{0}) > 0\), so hat der Graph \(G_{f}\) an der Stelle \(x_{0}\) ein relatives Minimum (Tiefpunkt).
Ist \(f'(x_{0}) = 0\) und \(f''(x_{0}) < 0\), so hat der Graph \(G_{f}\) an der Stelle \(x_{0}\) ein relatives Maximum (Hochpunkt).
\[A'(x) = - \ln x - 1\]
Ableitung der natürlichen Logarithmusfunktion
\[f(x) = \ln x \enspace (x > 0) \quad \Longrightarrow \quad f'(x) = \frac{1}{x}\]
(vgl. Merkhilfe)
\[A''(x) = -\frac{1}{x}\]
\[A''({\textstyle \frac{1}{e}}) = -\frac{1}{\frac{1}{e}} = -e\]
\[\left. \begin{align*} &A'({\textstyle \frac{1}{e}}) = 0 \\ &A''({\textstyle \frac{1}{e}}) < 0 \end{align*} \right\} \enspace \Rightarrow \enspace \text{lokales Maximum}\]
Mögliche Randextrema berücksichtigen:
Mit \(0 < x < 1\) ist die Funktion \(A(x)\) für \(x = 0\) und \(x = 1\) nicht definiert. Folglich kann es keine Randmaxima \(A(0)\) bzw. \(A(1)\) geben.
\(\Longrightarrow \quad\) Für \(\displaystyle x = \frac{1}{e}\) ist der Flächeninhalt \(A\) des Rechtecks maximal.
Seitenlängen des Rechtecks mit dem größten Flächeninhalt:
\[x = \frac{1}{e}\]
\[\begin{align*}f({\textstyle \frac{1}{e}}) &= -\ln({\textstyle \frac{1}{e}}) \\[0.8em] &= -\ln(e^{-1}) & &| \; \log_a(b^n) = n \cdot \log_a {b} \\[0.8em] &= (-1) \cdot (-\ln e) \\[0.8em] &= \ln e & &| \; \log_a{a} = 1 \\[0.8em] &= 1\end{align*}\]
Das Rechteck mit dem größten Flächeninhalt hat die Seitenlängen \(\displaystyle \frac{1}{e}\) LE und 1 LE (Längeneinheit).
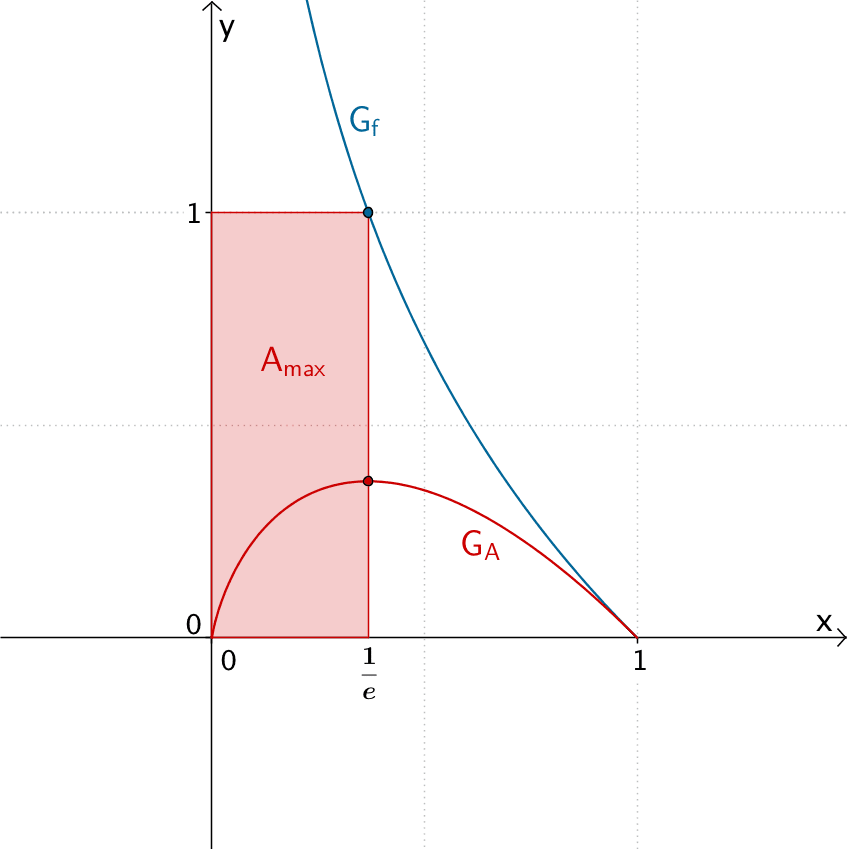
Graph der Funktion \(f\) und Graph der Funktion \(A\,\colon x \mapsto -x\cdot \ln x\) für \(0 < x < 1\), Rechteck mit größtem Flächeninhalt \(A_{\text{max}}\)


