Spiegelung eines Punktes an einem Punkt
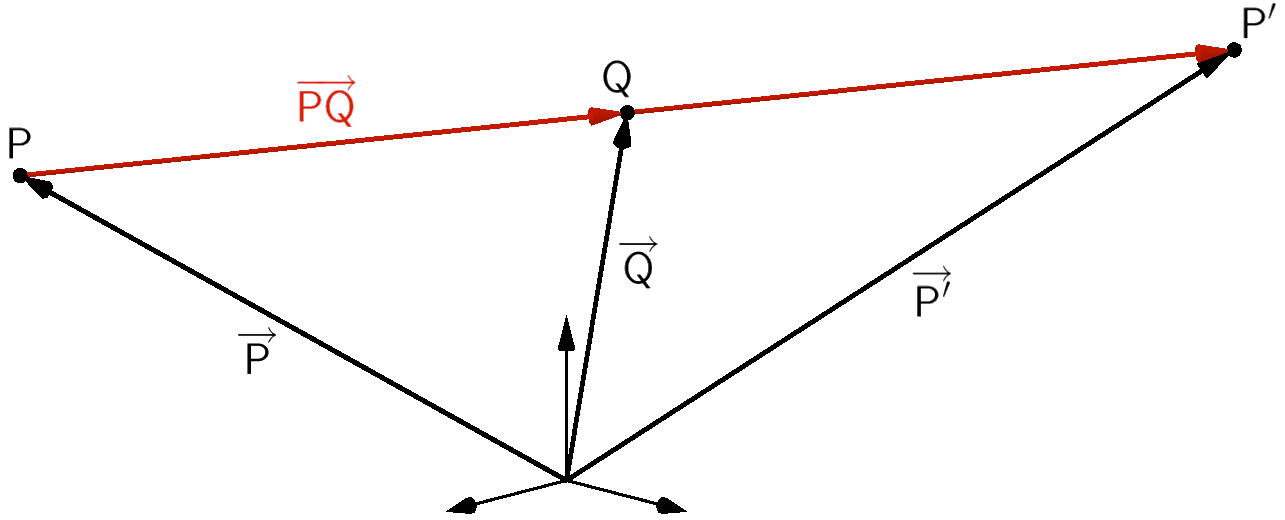
Die Entstehung eines Bildpunktes \(P'\), der durch Spiegelung eines Punktes \(P\) an einem Punkt \(Q\) hervorgeht, lässt sich durch Vektoraddition beschreiben.
\[\overrightarrow{P'} = \overrightarrow{P} + 2 \cdot \overrightarrow{PQ}\]
oder
\[\overrightarrow{P'} = \overrightarrow{Q} + \overrightarrow{PQ}\]
Beispielaufgabe
Gegeben seien die Punkte \(A(8|-1|5)\) und \(B(1|2|5)\).
Berechnen Sie die Koordinaten des Bildpunktes \(A'\), welcher durch Spiegelung des Punktes \(A\) an Punkt \(B\) entsteht.
Verbindungsvektor \(\overrightarrow{AB}\) ermitteln:
\(A(8|-1|5)\), \(B(1|2|5)\)
\[\overrightarrow{AB} = \overrightarrow{B} - \overrightarrow{A} = \begin{pmatrix} 1 \\ 2 \\ 5 \end{pmatrix} - \begin{pmatrix} 8 \\ -1 \\ 5 \end{pmatrix} = \begin{pmatrix} -7 \\ 3 \\ 0 \end{pmatrix}\]
Koordinaten des Bildpunktes \(A'\) berechnen:
\[\overrightarrow{A'} = \overrightarrow{A} + 2 \cdot \overrightarrow{AB} = \begin{pmatrix} 8 \\ -1 \\ 5 \end{pmatrix} + 2 \cdot \begin{pmatrix} -7 \\ 3 \\ 0 \end{pmatrix} = \begin{pmatrix} -6 \\ 5 \\ 5 \end{pmatrix}\]
\[\Longrightarrow \quad A'(-6|5|5)\]
oder
\[\overrightarrow{A'} = \overrightarrow{B} + \overrightarrow{AB} = \begin{pmatrix} 1 \\ 2 \\ 5 \end{pmatrix} + \begin{pmatrix} -7 \\ 3 \\ 0 \end{pmatrix} = \begin{pmatrix} -6 \\ 5 \\ 5 \end{pmatrix}\]
\[\Longrightarrow \quad A'(-6|5|5)\]


