Ermitteln Sie das Symmetrieverhalten des Graphen von \(f\) und geben Sie den Grenzwert von \(f\) für \(x \to +\infty\) an.
(3 BE)
Lösung zu Teilaufgabe 3b
Symmetrieverhalten von \(G_f\)
\[f(x) = \frac{\sin x}{x^2}\]
Symmetrie von Funktionsgraphen bzgl. des Koordinatensystems
Der Graph einer Funktion \(f\) ist
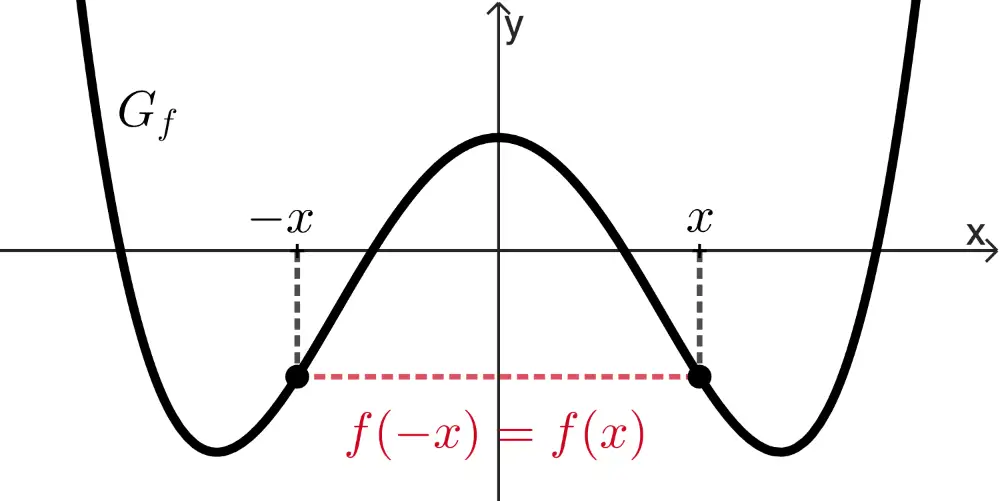
achsensymmetrisch bzgl. der \(\boldsymbol{y}\)-Achse,
wenn für alle \(x \in D_f\) gilt: \(f(-x) = f(x)\).
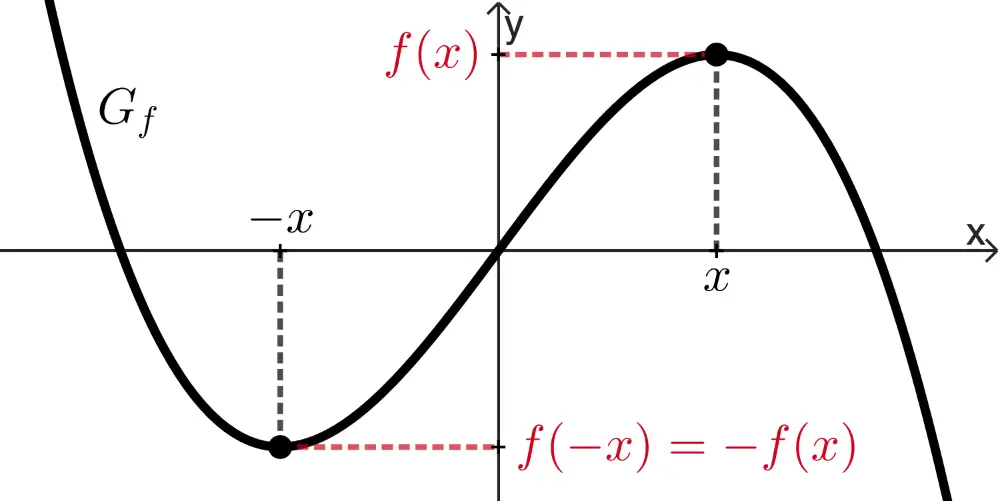
punktsymmetrisch bzgl. des Koordinatenursprungs,
wenn für alle \(x \in D_f\) gilt: \(f(-x) = -f(x)\)
\[f(-x) = \frac{\sin(-x)}{(-x)^2} = \frac{-\sin x}{x^2} = -f(x)\]
\(\Longrightarrow \quad\) Der Graph von \(f\) ist punktsymmetrisch zum Ursprung.
Grenzwert von \(f\) für \(x \to +\infty\)
\[f(x) = \frac{\sin x}{x^2}\]
\[\lim \limits_{x \, \to \, +\infty} f(x) = \lim \limits_{x \, \to \, +\infty} \bigg ( \frac{\overbrace{\enspace \sin x \enspace}^{[-1;1]}}{\underbrace{\enspace x^2 \enspace}_{\to \; +\infty}} \bigg ) = 0\]


