Der Flächeninhalt des Dreiecks \(ABC\) kann mit dem Term \(6 \cdot 6 - \dfrac{1}{2} \cdot 3 \cdot 3 - 2 \cdot \dfrac{1}{2} \cdot 3 \cdot 6\) berechnet werden. Veranschaulichen Sie diese Tatsache durch geeignete Eintragungen in der Abbildung.
(3 BE)
Lösung zu Teilaufgabe c
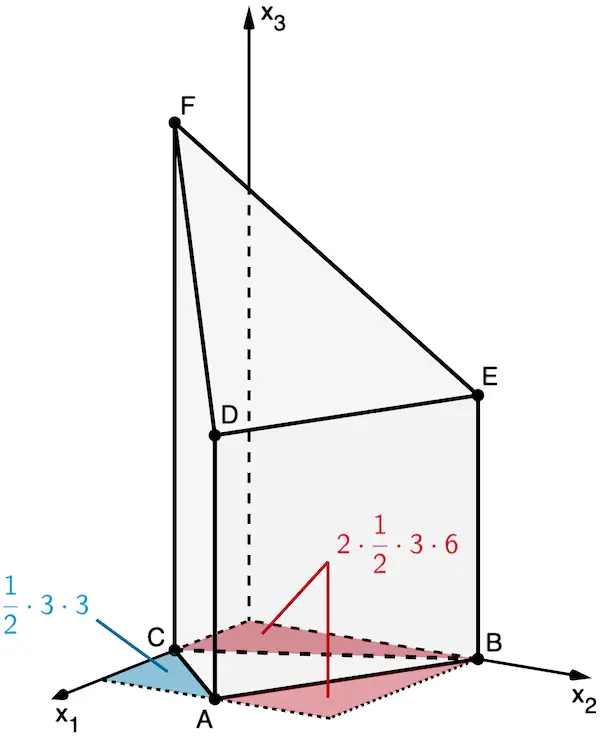
MIt \(A(6|3|0)\), \(B(0|6|0)\) und \(C(3|0|0)\) ergibt sich (nicht verlangt):
\[\begin{align*}A_{\text{ABC}} &= A_{\square} - \textcolor{#0087c1}{A_{\triangle}} - \textcolor{#cc071e}{2 \cdot A_{\triangle}} \\[0.8em] &= 6 \cdot 6 - \textcolor{#0087c1}{\frac{1}{2} \cdot 3 \cdot 3} - \textcolor{#cc071e}{2 \cdot \frac{1}{2} \cdot 3 \cdot 6} \end{align*}\]


