Auf das Solarmodul fällt Sonnenlicht, das im Modell durch parallele Geraden dargestellt wird, die senkrecht zur Ebene \(E\) verlaufen. Das Solarmodul erzeugt auf der horizontalen Fläche einen rechteckigen Schatten. Zeigen Sie unter Verwendung einer geeignet beschrifteten Skizze, dass der Flächeninhalt des Schattens mithilfe des Terms \(\vert \overrightarrow{AB} \vert \cdot \frac{\vert \overrightarrow{AD} \vert}{\cos{\varphi}} \cdot (0{,}8\,\sf{m})^{2}\) berechnet werden kann.
(5 BE)
Lösung zu Teilaufgabe e
Flächeninhalt eines Rechtecks, Trigonometrische Beziehung im rechtwinkligen Dreieck
Das senkrecht auf das Solarmodul (Viereck \(ABCD\)) einfallende Sonnenlicht bildet die gegenüber der Horizontalen geneigten Seiten \([AD]\) und \([BC]\) verlängert ab.
Aus Teilaufgabe a ist bekannt, dass die Gerade \(AB\) parallel zur \(x_{1}x_{2}\)-Achse verläuft. Demnach werden die Seiten \([AB]\) und \([CD]\) in wahrer Länge abgebildet.
![Einfallendes Sonnenlicht, Strecke [AD], Schatten [A'D'] Einfallendes Sonnenlicht, Strecke [AD], Schatten [A'D']](/images/stories/B2017_PT_B_G_1/B2017_PT_B_G_1_e_2.png)
Aus den senkrecht einfallenden Sonnenstrahlen, der Strecke \([AD]\) und der Schattenlänge \([A'D']\) lässt sich ein rechtwinkliges Dreieck konstruieren, in dem der Neigungswinkel \(\varphi\) des Solarmoduls gegenüber der Horizontalen auftritt (vgl. Teilaufgabe d).
Es gilt:
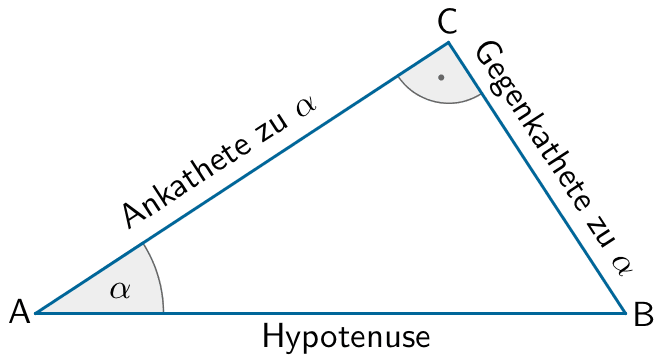
Trigonometrische Beziehungen im rechtwinkligen Dreieck
\[\sin \alpha = \frac{\text{Gegenkathete}}{\text{Hypotenuse}}\]
\[\cos \alpha = \frac{\text{Ankathete}}{\text{Hypotenuse}}\]
\[\tan \alpha = \frac{\text{Gegenkathete}}{\text{Ankathete}}\]
\[\cos{\varphi} = \frac{\overline{AD}}{\overline{A'D'}} \quad \Longleftrightarrow \quad \overline{A'D'} = \frac{\overline{AD}}{\cos{\varphi}}\]
Flächeninhalt des Schattens in FE (Flächeneinheiten):
Betrag eines Vektors
\[ \vert \overrightarrow{a} \vert = \sqrt{\overrightarrow{a} \circ \overrightarrow{a}} = \sqrt{{a_1}^2 + {a_2}^2 + {a_3}^2}\]
(vgl. Merkhilfe)
\[\begin{align*}A_{\text{Schatten}} &= \overline{A'B'} \cdot \overline{A'D'} \; & &| \; \overline{A'B'} = \overline{AB} \\[0.8em] &= \overline{AB} \cdot \overline{A'D'} & &| \; \overline{A'D'} = \frac{\overline{AD}}{\cos{\varphi}} \\[0.8em] &= \overline{AB} \cdot \frac{\overline{AD}}{\cos{\varphi}} \\[0.8em] &= \vert \overrightarrow{AB} \vert \cdot \frac{\vert \overrightarrow{AD} \vert}{\cos{\varphi}} \end{align*}\]
Flächeninhalt des Schattens in m²:
Eine Längeneinheit entspricht \(0{,}8\,\sf{m}\) (vgl. Angabe). Folglich entspricht eine Flächeneinheit \((0{,}8\,\sf{m})^{2}\).
\[\Longrightarrow \quad A_{\text{Schatten}} = \vert \overrightarrow{AB} \vert \cdot \frac{\vert \overrightarrow{AD} \vert}{\cos{\varphi}} \cdot (0{,}8\,\sf{m})^{2}\]
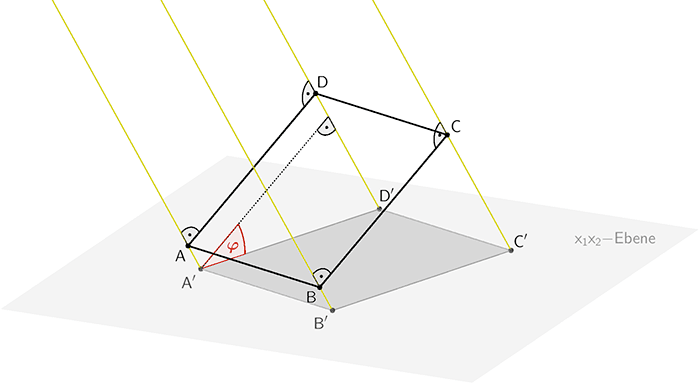
Entstehung des Schattens des Solarmoduls (Viereck \(ABCD\)) auf der horizontalen Fläche (\(x_{1}x_{2}\text{-Ebene}\))


