Ein Federball wird von einem Spieler in Hälfte A im Abstand von 1 m zur Netzebene in einer Höhe von 2,60 m geschlagen und trifft im Abstand von 3 m zur Netzebene in Hälfte B senkrecht zum Boden auf diesem auf. Ermitteln Sie die zugehörigen Werte von \(a\), \(b\) und \(c\).
(4 BE)
Lösung zu Teilaufgabe 3b
\(h(x) = a \cdot \sqrt{b-x} + c\) mit \(a,b,c \in \mathbb R\)
Analyse der Angabe:
„wird von einem Spieler in Hälfte A im Abstand von 1 m zur Netzebene in einer Höhe von 2,60 m geschlagen"
Abschlag im Punkt \((\textcolor{#cc071e}{-1}|\textcolor{#0087c1}{2{,}6})\)
\[\begin{align*}\Rightarrow\; h(\textcolor{#cc071e}{-1}) &= \textcolor{#0087c1}{2{,}6} \\[0.8em] a \cdot \sqrt{b- \textcolor{#cc071e}{(-1)}} + c &= \textcolor{#0087c1}{2{,}6} &&\text{(I)} \end{align*}\]
„trifft im Abstand von 3 m zur Netzebene in Hälfte B senkrecht zum Boden auf diesem auf."
Auftreffen im Punkt \((\textcolor{#cc071e}{3}|\textcolor{#0087c1}{0})\)
\[\begin{align*}\Rightarrow\; h(\textcolor{#cc071e}{3}) &= \textcolor{#0087c1}{0} \\[0.8em] a \cdot \sqrt{b- \textcolor{#cc071e}{3}} + c &= \textcolor{#0087c1}{0} &&\text{(II)} \end{align*}\]
\(\lim \limits_{x\,\to\,\textcolor{#cc071e}{3}} h'(x) = \textcolor{#e9b509}{-\infty}\) (vgl. Teilaufgabe 1c)
Ableitungen der Grundfunktionen
\[c' = 0 \enspace (c \in \mathbb R)\]
\[\left( x^r \right)' = r \cdot x^{r - 1} \enspace (r \in \mathbb R)\]
\[\left( \sqrt{x} \right)' = \frac{1}{2\sqrt{x}}\]
\[\left( \sin{x} \right)' = \cos{x}\]
\[\left( \cos{x} \right)' = -\sin{x}\]
\[\left( \ln{x} \right)' = \frac{1}{x}\]
\[\left( \log_{a}{x}\right)' = \frac{1}{x \cdot \ln{a}}\]
\[\left( e^x \right)' = e^x\]
\[\left(a^x \right)' = a^x \cdot \ln{a}\]
Faktorregel
\[\begin{align*}f(x) &= a \cdot \textcolor{#0087c1}{u(x)} \\[0.8em] f'(x) &= a \cdot \textcolor{#0087c1}{u'(x)}\end{align*}\]
Summenregel
\[\begin{align*}f(x) &= \textcolor{#0087c1}{u(x)} + \textcolor{#cc071e}{v(x)} \\[0.8em] f'(x) &= \textcolor{#0087c1}{u'(x)} + \textcolor{#cc071e}{v'(x)}\end{align*}\]
Produktregel
\[\begin{align*}f(x) &= \textcolor{#0087c1}{u(x)} \cdot \textcolor{#cc071e}{v(x)} \\[0.8em] f'(x) &= \textcolor{#0087c1}{u'(x)} \cdot \textcolor{#cc071e}{v(x)} + \textcolor{#0087c1}{u(x)} \cdot \textcolor{#cc071e}{v'(x)}\end{align*}\]
Quotientenregel
\[\begin{align*}f(x) &= \dfrac{\textcolor{#0087c1}{u(x)}}{\textcolor{#cc071e}{v(x)}} \\[0.8em] f'(x) &= \dfrac{\textcolor{#0087c1}{u'(x)} \cdot \textcolor{#cc071e}{v(x)} - \textcolor{#0087c1}{u(x)} \cdot \textcolor{#cc071e}{v'(x)}}{[\textcolor{#cc071e}{v(x)}]^{2}}\end{align*}\]
Kettenregel
\[\begin{align*}f(x) &= \textcolor{#0087c1}{u(}\textcolor{#cc071e}{v(x)}\textcolor{#0087c1}{)} \\[0.8em] f'(x) &= \textcolor{#0087c1}{u'(}\textcolor{#cc071e}{v(x)}\textcolor{#0087c1}{)} \cdot \textcolor{#cc071e}{v'(x)}\end{align*}\]
\[h'(x) = a \cdot \frac{1}{2\sqrt{b-x}} \cdot (-1) = -\frac{a}{2\sqrt{b-x}}\]
\[\lim \limits_{x\,\to\,\textcolor{#cc071e}{3}} -\frac{a}{2\sqrt{b-x}} = \textcolor{#e9b509}{-\infty} \; \Rightarrow \; b = 3\]
Nur mit \(b = 3\) nähert sich der Nenner \(2\sqrt{b-x}\) für \(x \to \textcolor{#cc071e}{3}\) dem Wert \(0^+\) an, sodass sich zusätzlich mit \(a > 0\) der Grenzwert \(\lim \limits_{x\,\to\,\textcolor{#cc071e}{3}} h'(x) = \textcolor{#e9b509}{-\infty}\) ergibt.
Das bedeutet, dass mit \(b = 3\) und \(a > 0\) die Steigung des Graphen von \(h\) für \(x \to \textcolor{#cc071e}{3}\) beliebig große negative Werte annimmt und somit der Graph von \(h\) im Punkt \((\textcolor{#cc071e}{3}|0)\) senkrecht zur \(x\)-Achse ist (vgl. Teilaufgabe 1c).
\(b = 3\) in Gleichungen (I) und (II) eingesetzt:
\[\; \text{(I)} \quad a \cdot \sqrt{3 + 1} + c = 2{,}6 \; \Leftrightarrow \; 2a + c = 2{,}6\]
\[\text{(II)} \quad a \cdot \sqrt{3- 3} + c = 0 \; \Leftrightarrow \; c = 0\]
\(c = 0\) in \(\text{(I)}\): \(2a=2{,}6 \; \Leftrightarrow \; a = 1{,}3\)
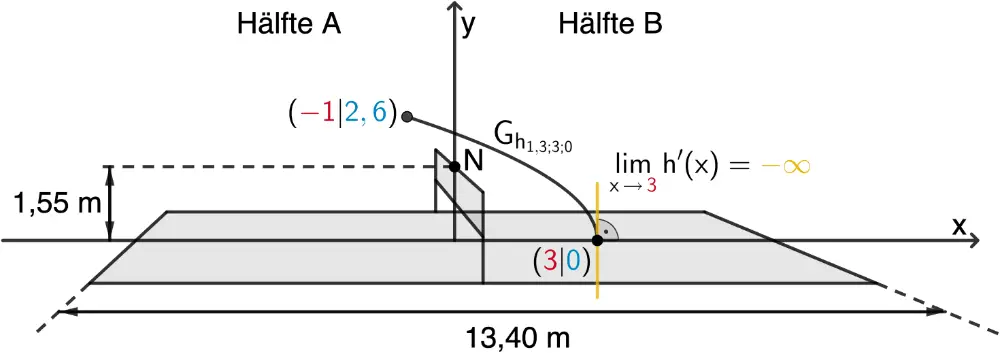ergänzende Darstellung
Flugbahn des Federballs, die im Modell durch den Graphen der Funktion \(h_{1{,}3;3;0}\colon x \mapsto 1{,}3 \cdot \sqrt{3-x}\) beschrieben wird.
Abschlag im Punkt \((\textcolor{#cc071e}{-1}|\textcolor{#0087c1}{2{,}6})\) und senkrechtes Auftreffen auf dem Boden im Punkt \((\textcolor{#cc071e}{3}|\textcolor{#0087c1}{0})\)
