Gegeben sind die Punkte \(R\,(8|5|1)\), \(S\,(-4|-1|1)\) und \(T_u\,(u|4|3)\) mit \(u \in \mathbb R\).
Bestimmen Sie einen Wert von \(u\) so, dass die drei Punkte ein gleichschenkliges Dreieck mit der Basis \([RS]\) bilden.
(4 BE)
Lösung zu Teilaufgabe 2
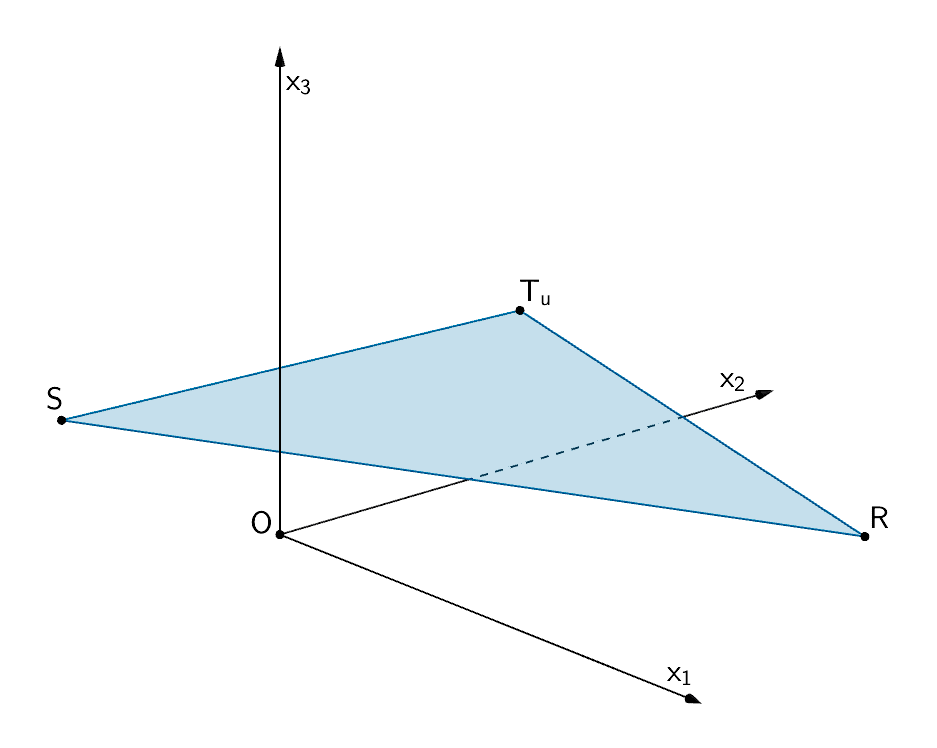
Die Punkte \(R\,(8|5|1)\), \(S\,(-4|-1|1)\) und \(T_u\,(u|4|3)\) bilden dann ein gleichschenkliges Dreieck mit der Basis \([RS]\), wenn die Seiten \([RT_u]\) und \([ST_u]\) gleich lang sind.
Betrag eines Vektors
\[ \vert \overrightarrow{a} \vert = \sqrt{\overrightarrow{a} \circ \overrightarrow{a}} = \sqrt{{a_1}^2 + {a_2}^2 + {a_3}^2}\]
(vgl. Merkhilfe)
\[\begin{align*} \overline{RT_u} &= \overline{ST_u} \\[0.8em] \vert \overrightarrow{RT_u} \vert &= \vert \overrightarrow{ST_u} \vert \\[0.8em] \vert \overrightarrow{T_u} - \overrightarrow{R} \vert &= \vert \overrightarrow{T_u} - \overrightarrow{S} \vert \\[0.8em] \left| \begin{pmatrix} u \\ 4 \\ 3 \end{pmatrix} - \begin{pmatrix} 8 \\ 5 \\ 1 \end{pmatrix} \right| &= \left| \begin{pmatrix} u \\ 4 \\ 3 \end{pmatrix} - \begin{pmatrix} -4 \\ -1 \\ 1 \end{pmatrix} \right| \\[0.8em] \left| \begin{pmatrix} u - 8 \\ -1 \\ 2 \end{pmatrix} \right| &= \left| \begin{pmatrix} u + 4 \\ 5 \\ 2 \end{pmatrix} \right| \\[0.8em] \sqrt{(u - 8)^2 + (-1)^2 + 2^2} &= \sqrt{(u + 4)^2 + 5^2 + 2^2} & &|\;(\dots)^2 \\[0.8em] (u - 8)^2 + 1 + 4 &= (u + 4)^2 + 25 + 4 \\[0.8em] u^2 - 16u + 69 &= u^2 + 8u + 45 & &| - u^2 + 16u - 45 \\[0.8em] 24 &= 24u & &| : 24 \\[0.8em] 1 &= u \end{align*}\]
\[\Longrightarrow \quad T_1\,(1|4|3)\]
Die Punkte \(R\,(8|5|1)\), \(S\,(-4|-1|1)\) und \(T_1\,(1|4|3)\) bilden ein gleichschenkliges Dreieck mit der Basis \([RS]\).


