Zeigen Sie, dass der Graph der in \(\mathbb R\) definierten Funktion \(g \colon x \mapsto x^{2} \cdot \sin{x}\) punktsymmetrisch bezüglich des Koordinatenursprungs ist, und geben Sie den Wert des Integrals \(\displaystyle \int_{-\pi}^{\pi} x^{2} \cdot \sin{x}\, dx\) an.
(3 BE)
Lösung zu Teilaufgabe 2
Symmetrieverhalten einer Funktion, Bestimmtes Integral und Flächenbilanz
\[g(x) = x^{2} \cdot \sin{x}; \; D = \mathbb R\]
Nachweis der Punktsymmetrie des Graphen der Funktion \(g\)
Symmetrie von Funktionsgraphen bzgl. des Koordinatensystems
Der Graph einer Funktion \(f\) ist
achsensymmetrisch bzgl. der \(\boldsymbol{y}\)-Achse,
wenn für alle \(x \in D_f\) gilt: \(f(-x) = f(x)\).
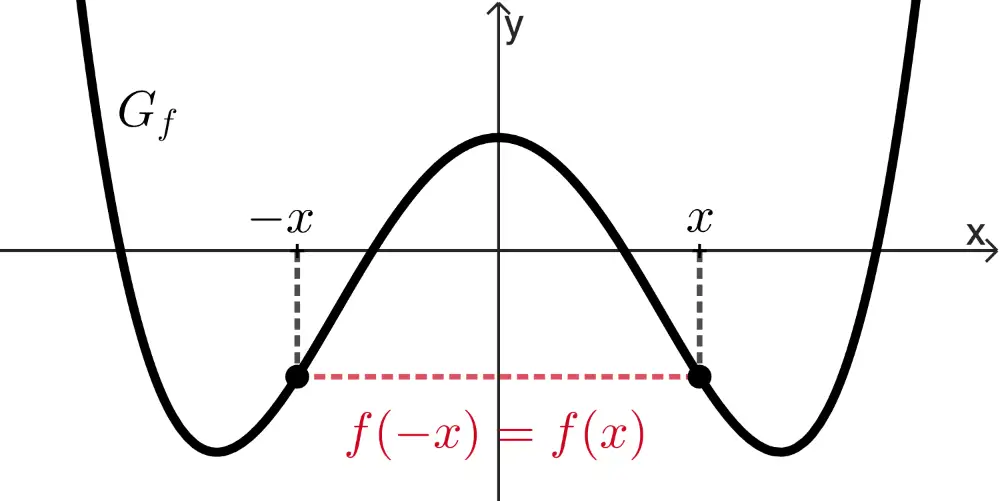
punktsymmetrisch bzgl. des Koordinatenursprungs,
wenn für alle \(x \in D_f\) gilt: \(f(-x) = -f(x)\)
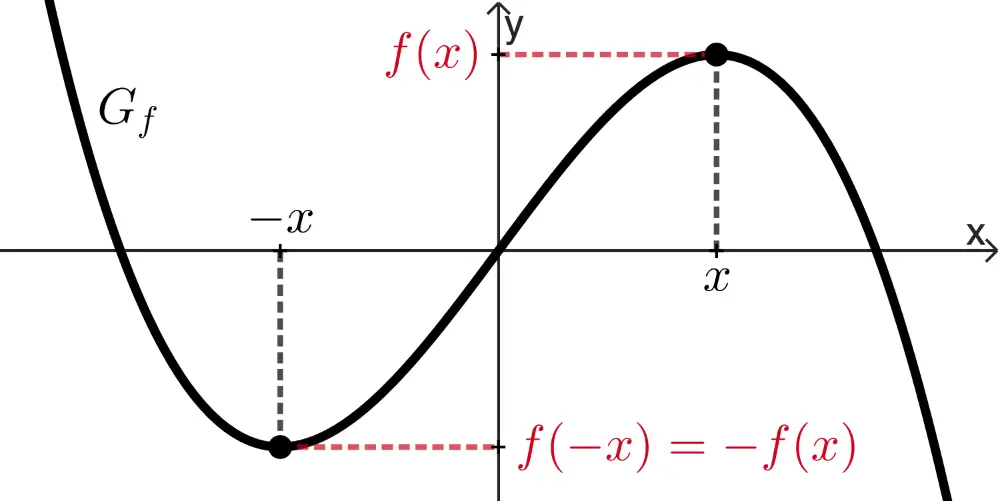
Der Graph der Funktion \(g\) ist punktsymmetrisch bezüglich des Koordinatenursprungs, falls gilt:
\[g(-x) = -g(x)\]
Unter Berücksichtigung der Punktsymmetrie des Graphen der Sinusfunktion \(x \mapsto \sin x\) lässt sich die Punktsymmetrie des Graphen der Funktion \(g\) nachweisen.
Das heißt, es gilt: \(\sin(-x) = -\sin x\).
\[\begin{align*} g(-x) &= (-x)^{2} \cdot \sin(-x) & &| \; \sin(-x) = -\sin{x} \\[0.8em] &= -x^{2} \cdot \sin{x} \\[0.8em] &= -g(x) \end{align*}\]
\(\Longrightarrow \quad\)Der Graph der Funktion \(g\) ist punktsymmetrisch bezüglich des Koordinatenursprungs.
Wert des Integrals \(\displaystyle \int_{-\pi}^{\pi} x^{2} \cdot \sin{x}\, dx\)
\[\int_{-\pi}^{\pi} x^{2} \cdot \sin{x}\, dx = 0\]
Begründung (nicht verlangt):
Ist \(f\) eine Funktion, deren Graph \(G_{f}\) bezüglich des Koordinatenursprungs punktsymmetrisch verläuft, so ist der Wert des bestimmten Integrals \(\displaystyle \int_{-a}^{a} f(x)\, dx\) mit den zum Koordinatenursprung symmetrischen Integrationsgrenzen \(-a\) und \(a\) \((a \in \mathbb R)\) gleich Null.
Der zum Koordinatenursprung punktsymmetrische Graph der Funktion \(g\) verläuft im Intervall \([-\pi;0]\) unterhalb der \(x\)-Achse und im Intervall \([0;\pi]\) oberhalb der \(x\)-Achse. Die Flächeninhalte, welche \(G_{g}\) im Intervall \([-\pi;0]\) bzw. im Intervall \([0;\pi]\) mit der \(x\)-Achse einschließt, sind dem Betrag nach gleich groß. Das Integral \(\displaystyle \int_{-\pi}^{\pi} x^{2} \cdot \sin{x}\, dx\) kann als Flächenbilanz dieser Flächeninhalte betrachtet werden. Dabei wird der unterhalb der \(x\)-Achse liegende Flächeninhalt negativ gezählt \((-A)\) und der oberhalb der \(x\)-Achse liegende Flächeninhalt positiv gezählt \((+A)\). Folglich ist die Flächenbilanz der Flächeninhalte gleich Null.
\[\int_{-\pi}^{\pi} x^{2} \cdot \sin{x}\, dx = \underbrace{\int_{-\pi}^{0} x^{2} \cdot \sin{x}\, dx}_{\Large{-A}} + \underbrace{\int_{0}^{\pi} x^{2} \cdot \sin{x}\, dx}_{\Large{+A}} = 0\]
![Graph der Funktion g, Flächenbilanz für x ∈ [-π;π] Graph der Funktion g, Flächenbilanz für x ∈ [-π;π]](/images/stories/B2016_PT_A_A_1/B2016_PT_A_A_1_2.png)
Graph der Funktion \(g \colon x \mapsto x^{2} \cdot \sin{x}\) und Flächenbilanz des Integrals \(\displaystyle \int_{-\pi}^{\pi} x^{2} \cdot \sin{x}\, dx\)


