Gegeben sind die in \(\mathbb R\) definierten Funktionen \(f\), \(g\) und \(h\) mit \(f(x) = x^2 - x + 1\), \(g(x) = x^3 - x + 1\) und \(h(x) = x^4 + x^2 + 1\).
Abbildung 1 zeigt den Graphen einer der drei Funktionen. Geben Sie an, um welche Funktion es sich handelt. Begründen Sie, dass der Graph die anderen beiden Funktionen nicht darstellt.
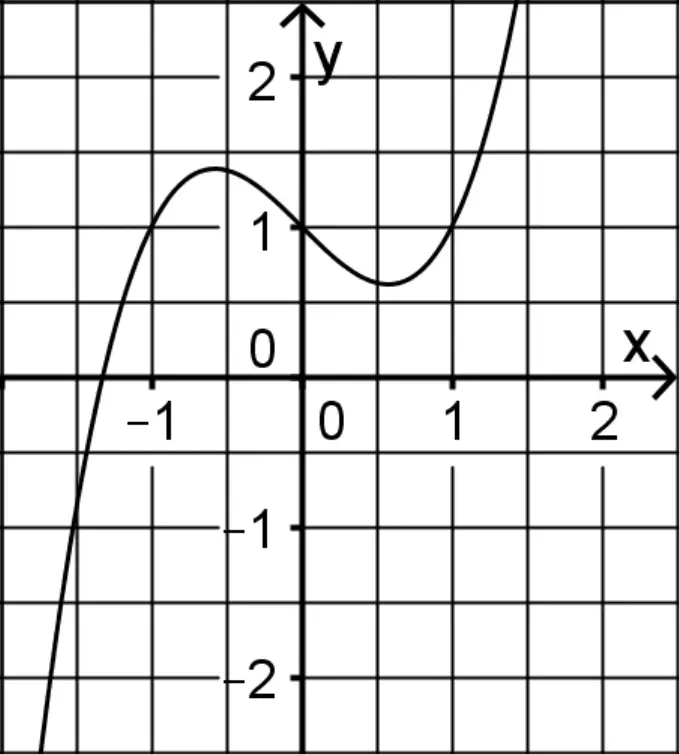Abb. 1
(3 BE)
Lösung zu Teilaufgabe 2a
Zuordnen von Funktionstermen
\[f(x) = x^2 - x + 1\,; \quad D _{f} = \mathbb R\]
\[g(x) = x^3 - x + 1\,; \quad D _{g} = \mathbb R\]
\[h(x) = x^4 + x^2 + 1\,; \quad D _{h} = \mathbb R\]
Abbildung 1 zeigt den Graphen der Funktion \(g\).
Funktion \(f\) kommt nicht in Frage, da
1) eine quadratische Funktion genau einen Extrempunkt (Scheitelpunkt) hat.
2) der Graph von \(f\) für \(x \to \pm\infty\) gegen \(+\infty\) geht.
\[\begin{align*} \lim \limits_{x \, \to \pm \infty} f(x) &= \lim \limits_{x \, \to \, \pm \infty} x^2 - x +1 \\[0.8em] &= \lim \limits_{x \, \to \, \pm \infty} x^2 \underbrace{\left( 1 - \frac{1}{x} + \frac{1}{x^{2}} \right)}_{\to \, 1} = +\infty \end{align*}\]
Funktion \(h\) kommt nicht in Frage, da
1) der Graph von \(h\) achsensymmetrisch zur \(y\)-Achse ist (ganzrationale Funktion mit ausschließlich geraden Exponenten).
Symmetrie von Funktionsgraphen bzgl. des Koordinatensystems
Der Graph einer Funktion \(f\) ist
achsensymmetrisch bzgl. der \(\boldsymbol{y}\)-Achse,
wenn für alle \(x \in D_f\) gilt: \(f(-x) = f(x)\).
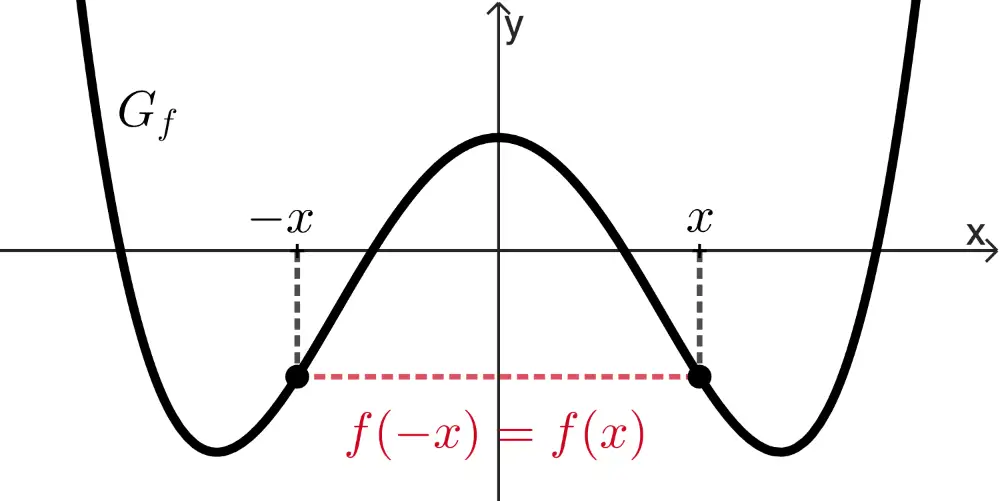
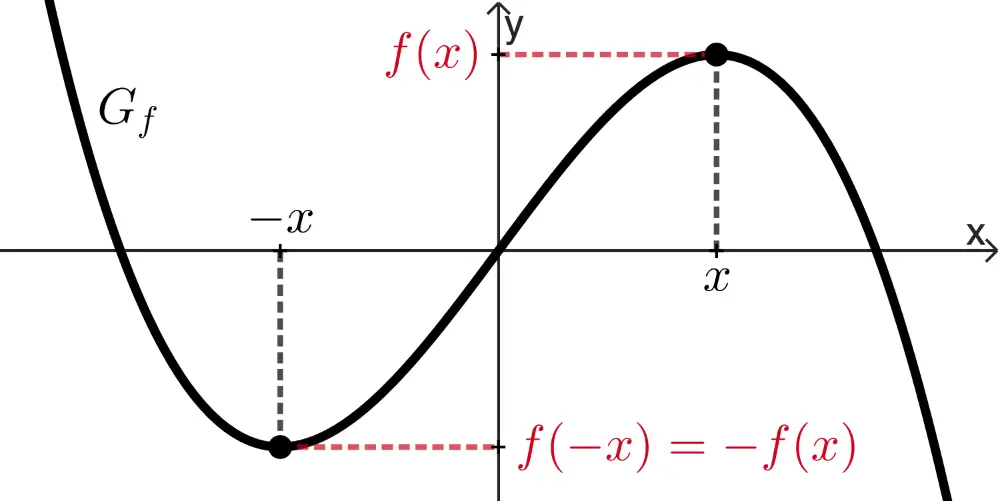
punktsymmetrisch bzgl. des Koordinatenursprungs,
wenn für alle \(x \in D_f\) gilt: \(f(-x) = -f(x)\)
\[h(-x) = (-x)^{4} + (-x)^{2} + 1 = x^{4} + x^{2} + 1 = h(x)\]
2) der Graph von \(h\) für \(x \to \pm\infty\) gegen \(+\infty\) geht.
\[\begin{align*} \lim \limits_{x \, \to \pm \infty} h(x) &= \lim \limits_{x \, \to \, \pm \infty} x^{4} + x^{2} +1 \\[0.8em] &= \lim \limits_{x \, \to \, \pm \infty} x^{4} \underbrace{\left( 1 + \frac{1}{x^{2}} + \frac{1}{x^{4}} \right)}_{\to \, 1} = +\infty \end{align*}\]
