Die Gerade \(g\) berührt die Kugel im Punkt \(B(-3|8|2)\). Ermitteln Sie eine mögliche Gleichung von \(g\).
(2 BE)
Lösung zu Teilaufgabe 1b
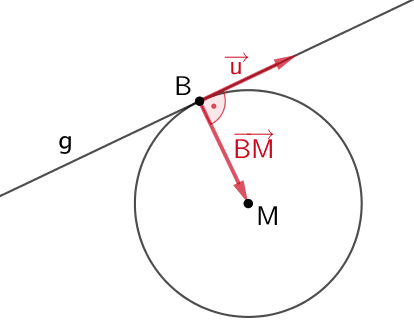
Es gibt unendliche viele Geraden, welche die Kugel im Punkt \(B\) berühren. Da eine Tangente an eine Kugel stets senkrecht zum Kugelradius verläuft, gilt für alle diese Geraden, dass der Richtungsvektor \(\overrightarrow{u}\) und der Verbindungsvektor \(\overrightarrow{BM}\) zueinander senkrecht sind.
Folglich muss das Skalarprodukt der Vektoren \(\overrightarrow{u}\) und \(\overrightarrow{BM}\) gleich Null sein.
Anwendung des Skalarprodukts:
Orthogonale (zueinander senkrechte) Vektoren (vgl. Merkhilfe)
\[\overrightarrow{a} \perp \overrightarrow{b} \; \Leftrightarrow \; \overrightarrow{a} \circ \overrightarrow{b} \quad (\overrightarrow{a} \neq \overrightarrow{0},\; \overrightarrow{b} \neq \overrightarrow{0})\]
\[\overrightarrow{u} \perp \overrightarrow{BM} \quad \Longleftrightarrow \quad \overrightarrow{u} \circ \overrightarrow{BM} = 0\]
Mit dem Aufpunkt \(B(-3|8|2)\) und dem Richtungsvektor \(\overrightarrow{u}\) ist einen Gleichung der Geraden \(g\) in Parameterform gegeben durch:
Gleichung einer Gerade / Strecke in Parameterform
Jede Gerade \(g\) kann durch eine Gleichung in der sogenannten Parameterform
\(g \colon \overrightarrow{X} = \overrightarrow{A} + \lambda \cdot \overrightarrow{u} \enspace\) mit dem Parameter \(\lambda \in \mathbb R\) beschrieben werden.
Dabei ist \(\overrightarrow{A}\) der Ortsvektor eines Aufpunkts (Stützvektor) und \(\overrightarrow{u}\) ein Richtungsvektor der Gerade \(g\).
Gleichung einer Strecke \([AB]\) in Parameterform:
\[\overrightarrow{X} = \overrightarrow{A} + \lambda \cdot \overrightarrow{AB}, \; \textcolor{#cc071e}{\lambda \in [0;1]} \]
\[g \colon \overrightarrow{X} = \begin{pmatrix} -3 \\ 8 \\ 2 \end{pmatrix} + \lambda \cdot \overrightarrow{u}, \; \lambda \in \mathbb R\]
Verbindungsvektor \(\overrightarrow{BM}\) berechnen:
\(B(-3|8|2)\), \(M(1|4|0)\)
\[\overrightarrow{BM} = \overrightarrow{M} - \overrightarrow{B} = \begin{pmatrix} 1 \\ 4 \\ 0 \end{pmatrix} - \begin{pmatrix} -3 \\ 8 \\ 2 \end{pmatrix} = \begin{pmatrix} 4 \\ -4 \\ -2 \end{pmatrix}\]
Richtungsvektor \(\overrightarrow{u}\) durch Überlegung bestimmen:
\[\begin{align*} \overrightarrow{u} \circ \overrightarrow{BM} &= 0 \\[0.8em] \overrightarrow{u} \circ \begin{pmatrix} 4 \\ -4 \\ -2 \end{pmatrix} &= 0 \end{align*}\]
Es gibt unendlich viele Möglichkeiten für den Richtungsvektor \(\overrightarrow{u} = \begin{pmatrix} u_{1} \\ u_{2} \\ u_{3} \end{pmatrix}\).
Wählt man beispielsweise für die dritte Vektorkoordinate \(u_{3} = 0\), so muss \(u_{1} = u_{2}\) gelten, damit die Vektorgleichung \(\overrightarrow{u} \circ \begin{pmatrix} 4 \\ -4 \\ -2 \end{pmatrix} = 0\) erfüllt ist.
Denn es gilt:
Skalarprodukt
Unter dem Skalarprodukt \(\overrightarrow{a} \circ \overrightarrow{b}\) zweier Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) versteht man das Produkt aus den Beträgen der beiden Vektoren und dem Kosinus des von den Vektoren eingeschlossenen Winkels \(\varphi\).
\[\overrightarrow{a} \circ \overrightarrow{b} = \vert \overrightarrow{a} \vert \cdot \vert \overrightarrow{b} \vert \cdot \cos{\varphi} \quad (0^{\circ} \leq \varphi \leq 180^{\circ})\]
Berechnung eines Skalarprodukts im \(\boldsymbol{\mathbb R^{3}}\) (vgl. Merkhilfe)
\[\overrightarrow{a} \circ \overrightarrow{b} = \begin{pmatrix} a_{1} \\ a_{2} \\ a_{3} \end{pmatrix} \circ \begin{pmatrix} b_{1} \\ b_{2} \\ b_{3} \end{pmatrix} = a_{1}b_{1} + a_{2}b_{2} + a_{3}b_{3}\]
\[\begin{align*}\begin{pmatrix} u_{1} \\ u_{2} \\ 0 \end{pmatrix} \circ \begin{pmatrix} 4 \\ -4 \\ -2 \end{pmatrix} &= 0 \\[0.8em] u_{1} \cdot 4 + u_{2} \cdot (-4) + 0 \cdot (-2) &= 0 \\[0.8em] 4u_{1} - 4u_{2} &= 0 &&| \; u_{1} = u_{2} \\[0.8em] 0 &= 0 \end{align*}\]
Beispielsweise ist \(\overrightarrow{u} = \begin{pmatrix} 1 \\ 1 \\ 0 \end{pmatrix}\) ein möglicher Richtungsvektor der Gleichung der Geraden \(g\), ebenso wie \(\begin{pmatrix} 2 \\ 2 \\ 0 \end{pmatrix}\) oder \(\begin{pmatrix} 3 \\ 3 \\ 0 \end{pmatrix}\) oder\( \begin{pmatrix} -10 \\ -10 \\ 0 \end{pmatrix}\) usw.
Eine mögliche Gleichung der Geraden \(g\) ist also:
\[g \colon \overrightarrow{X} = \begin{pmatrix} -3 \\ 8 \\ 2 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 1 \\ 1 \\ 0 \end{pmatrix}, \; \lambda \in \mathbb R\]


