Die Abbildung zeigt modellhaft einen Austellungspavillon, der die Form einer geraden vierseitigen Pyramide mit quadratischer Grundfläche hat und auf einer horizontalen Fläche steht. Das Dreieck \(BCS\) beschreibt im Modell die südliche Außenwand des Pavillons. Im Koordinatensystem entspricht eine Längeneinheit 1 m, d.h. die Grundfläche des Pavillons hat eine Seitenlänge von 12 m.
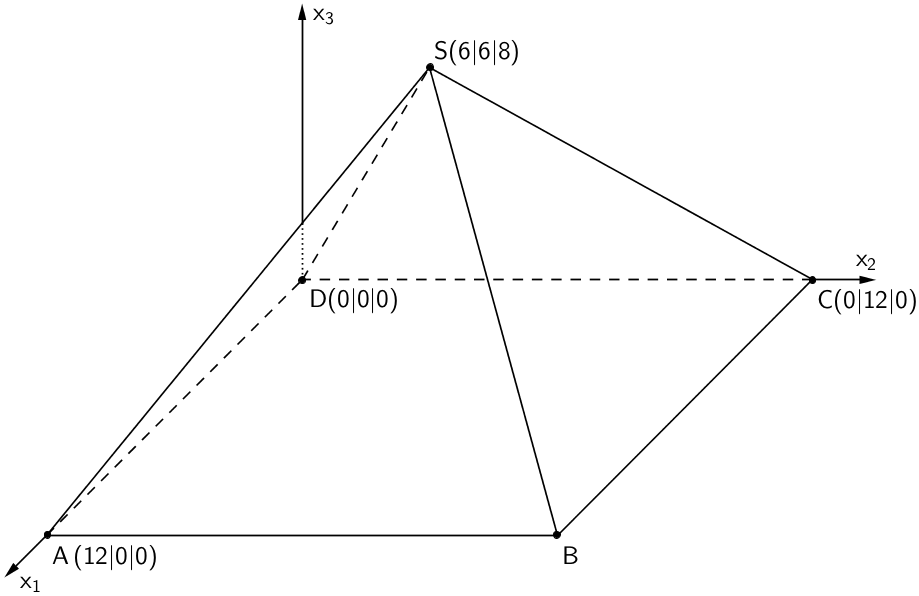
Geben Sie die Koordinaten des Punkts \(B\) an und bestimmen Sie das Volumen des Pavillons.
(3 BE)
Lösung zu Teilaufgabe 1a
Koordinaten des Punktes \(B\)
1. Lösungsansatz: Vektoraddition
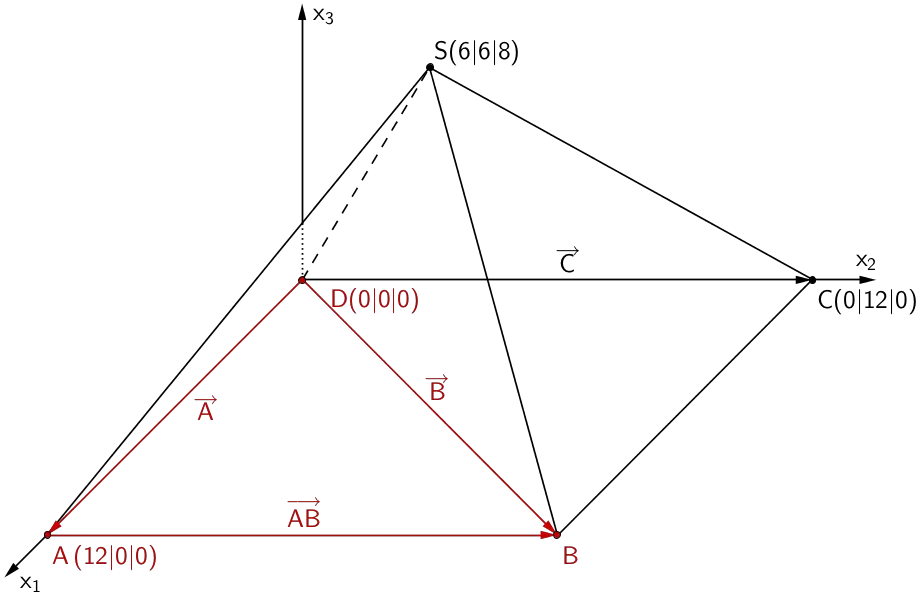
Die Koordinaten des Punktes \(B\) lassen sich durch Vektoraddition berechnen.
\[\begin{align*} \overrightarrow{B} &= \overrightarrow{A} + \overrightarrow{AB} & &| \; \overrightarrow{AB} = \overrightarrow{C} \\[0.8em] &= \overrightarrow{A} + \overrightarrow{C} \\[0.8em] &= \begin{pmatrix} 12 \\ 0 \\ 0 \end{pmatrix} + \begin{pmatrix} 0 \\ 12 \\ 0 \end{pmatrix} \\[0.8em] &= \begin{pmatrix} 12 \\ 12 \\ 0 \end{pmatrix} \end{align*}\]
\[\Longrightarrow \quad B\,(12|12|0)\]
2. Lösungsansatz: Argumentation mithilfe der Skizze und der Angabe

Gerade vierseitige Pyramide \(ABCDS\) mit quadratischer Grundfläche
Der Skizze sowie dem Text der Angabe entnimmt man folgende mathematische Sachverhalte:
Quadrat \(ABCD\)
\[B \in x_1x_2\text{-Ebene}\]
\[\begin{align*} \Longrightarrow \quad x_{1_B} &= x_{1_A} \\[0.8em] x_{2_B} &= x_{2_C} \\[0.8em] x_{3_B} &= 0 \end{align*}\]
\[\Longrightarrow \quad B\,(12|12|0)\]
Volumen des Pavillons
1. Lösungsansatz: \(V = \frac{1}{3} \cdot G \cdot h\)
Volumen einer Pyramide
\[V = \frac{1}{3} \cdot G \cdot h\]
\(G\): Flächeninhalt der Grundfläche der Pyramide
\(h\): Höhe der Pyramide
Die Höhe \(h\) einer Pyramide ist der Abstand der Spitze der Pyramide von der Ebene, in der die Grundfläche \(G\) liegt.
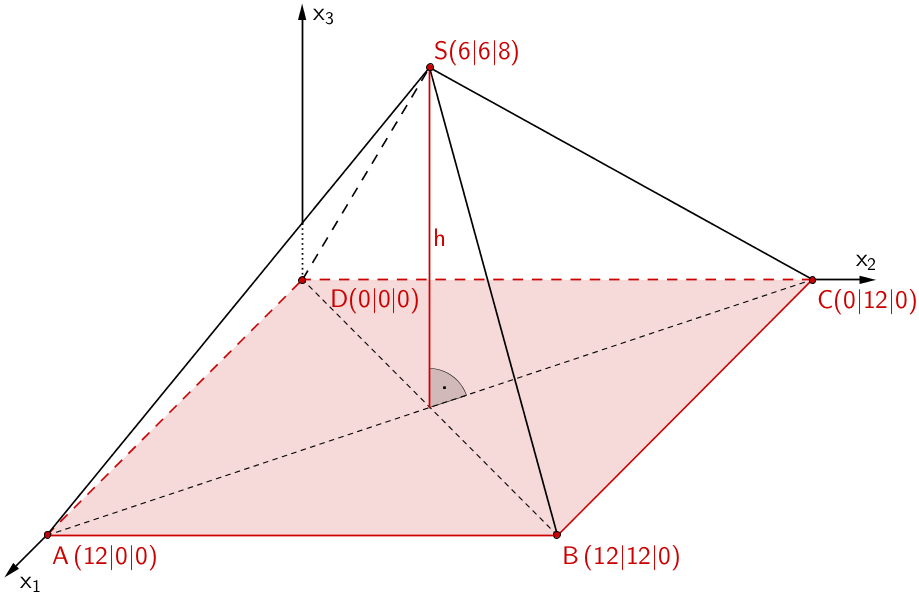
Quadratische Grundfläche \(ABCD\) und Höhe \(h\) der geraden vierseitigen Pyramide \(ABCDS\)
\[V_{ABCDS} = \frac{1}{3} \cdot A_{ABCD} \cdot h\]
Flächeninhalt \(A_{ABCD}\) der Grundfläche berechnen:
Die Grundfläche des Pavillons hat eine Seitenlänge von 12 m (siehe Angabe).
\[A_{ABCD} = 12^2 = 144\]
Höhe \(h\) der Pyramide \(ABCDS\) bestimmen:
\[h = d\,(S;x_1x_2\text{-Ebene}) = x_{3_S} = 8\]
Volumne der Pyramide \(ABCDS\) berechnen:
\[\begin{align*} V_{ABCDS} &= \frac{1}{3} \cdot A_{ABCD} \cdot h \\[0.8em] &= \frac{1}{3} \cdot 144 \cdot 8 \\[0.8em] &= 384 \end{align*}\]
Das Volumne des Pavillons beträgt 384 m³.
2. Lösungsansatz: Anwenden des Spatprodukts
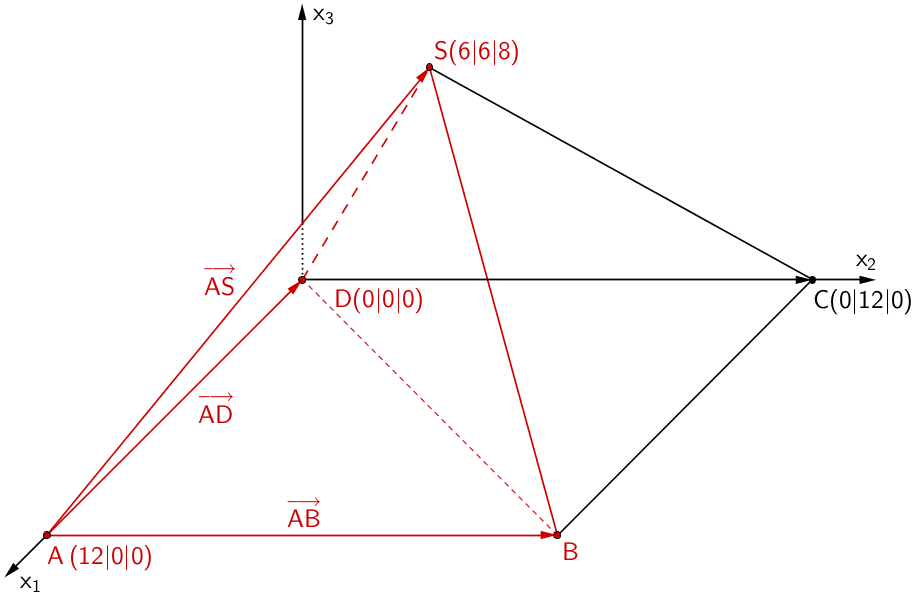
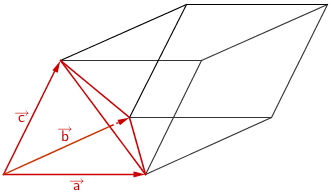
Die drei linear unabhängigen Vektoren \(\overrightarrow{AB}\), \(\overrightarrow{AD}\) und \(\overrightarrow{AS}\) spannen einen Spat auf. Das Volumen der dreiseitigen Pyramide \(ABDS\) beträgt ein sechstel des Volumens des Spats.
Anwendung des Vekorprodukts - Spatprodukt (vgl. Merkhilfe)
Volumen eines Spats
\[V_{\text{Spat}} = \left| \left( \overrightarrow{a} \times \overrightarrow{b} \right) \circ \overrightarrow{c} \; \right|\]
Volumen einer dreiseitigen Pyramide
\[V_{\text{Pyramide}} = \frac{1}{6} \left| \left( \overrightarrow{a} \times \overrightarrow{b} \right) \circ \overrightarrow{c} \; \right|\]
\[\begin{align*} V_{ABCDS} &= 2 \cdot \frac{1}{6} \cdot \left| \left( \overrightarrow{AB} \times \overrightarrow{AD} \right) \circ \overrightarrow{AS}\; \right| \\[0.8em] &= \frac{1}{3} \cdot \left| \left( \overrightarrow{AB} \times \overrightarrow{AD} \right) \circ \overrightarrow{AS}\; \right| \end{align*}\]
Vektoren \(\overrightarrow{AB}\), \(\overrightarrow{AD}\) und \(\overrightarrow{AS}\) bestimmen:
\[A\,(12|0|0)\,,\enspace B\,(12|12|0)\,, \enspace D\,(0|0|0)\,,\enspace S\,(6|6|8)\]
\[\overrightarrow{AB} = \overrightarrow{B} - \overrightarrow{A} = \begin{pmatrix} 12 \\ 12 \\ 0 \end{pmatrix} - \begin{pmatrix} 12 \\ 0 \\ 0 \end{pmatrix} = \begin{pmatrix} 0 \\ 12 \\ 0 \end{pmatrix}\]
\[\overrightarrow{AD} = \overrightarrow{D} - \overrightarrow{A} = \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix} - \begin{pmatrix} 12 \\ 0 \\ 0 \end{pmatrix} = \begin{pmatrix} -12 \\ 0 \\ 0 \end{pmatrix}\]
\[\overrightarrow{AS} = \overrightarrow{S} - \overrightarrow{A} = \begin{pmatrix} 6 \\ 6 \\ 8 \end{pmatrix} - \begin{pmatrix} 12 \\ 0 \\ 0 \end{pmatrix} = \begin{pmatrix} -6 \\ 6 \\ 8 \end{pmatrix}\]
Volumen der Pyramide \(ABCDS\) berechnen:
Vektorprodukt (Kreuzprodukt)
Das Vektorprodukt \(\overrightarrow{a} \times \overrightarrow{b}\) zweier Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) erzeugt einen neuen Vektor \(\overrightarrow{c} = \overrightarrow{a} \times \overrightarrow{b}\) mit den Eigenschaften:
\(\overrightarrow{c}\) ist sowohl zu \(\overrightarrow{a}\) als auch zu \(\overrightarrow{b}\) senkrecht.
\[\overrightarrow{c} = \overrightarrow{a} \times \overrightarrow{b} \quad \Longrightarrow \quad \overrightarrow{c} \perp \overrightarrow{a}, \enspace \overrightarrow{c} \perp \overrightarrow{b}\]
Der Betrag des Vektorprodukts zweier Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) ist gleich dem Produkt aus den Beträgen der Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) und dem Sinus des von ihnen eingeschlossenen Winkels \(\varphi\).
\[\vert \overrightarrow{a} \times \overrightarrow{b} \vert = \vert \overrightarrow{a} \vert \cdot \vert \overrightarrow{b} \vert \cdot \sin{\varphi} \quad (0^{\circ} \leq \varphi \leq 180^{\circ})\]
Die Vektoren \(\overrightarrow{a}\), \(\overrightarrow{b}\) und \(\overrightarrow{c}\) bilden in dieser Reihenfolge ein Rechtssystem. Rechtehandregel: Weist \(\overrightarrow{a}\) in Richtung des Daumens und \(\overrightarrow{b}\) in Richtung des Zeigefingers, dann weist \(\overrightarrow{c} = \overrightarrow{a} \times \overrightarrow{b}\) in Richtung des Mittelfingers.
Berechnung eines Vektorprodukts im \(\boldsymbol{\mathbb R^{3}}\) (vgl. Merkhilfe)
\[\overrightarrow{a} \times \overrightarrow{b} = \begin {pmatrix} a_1 \\ a_2 \\ a_3 \end {pmatrix} \times \begin {pmatrix} b_1 \\ b_2 \\ b_3 \end {pmatrix} = \begin {pmatrix} a_2 \cdot b_3 - a_3 \cdot b_2 \\ a_3 \cdot b_1 - a_1 \cdot b_3 \\ a_1 \cdot b_2 - a_2 \cdot b_1 \end {pmatrix}\]
Skalarprodukt
Unter dem Skalarprodukt \(\overrightarrow{a} \circ \overrightarrow{b}\) zweier Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) versteht man das Produkt aus den Beträgen der beiden Vektoren und dem Kosinus des von den Vektoren eingeschlossenen Winkels \(\varphi\).
\[\overrightarrow{a} \circ \overrightarrow{b} = \vert \overrightarrow{a} \vert \cdot \vert \overrightarrow{b} \vert \cdot \cos{\varphi} \quad (0^{\circ} \leq \varphi \leq 180^{\circ})\]
Berechnung eines Skalarprodukts im \(\boldsymbol{\mathbb R^{3}}\) (vgl. Merkhilfe)
\[\overrightarrow{a} \circ \overrightarrow{b} = \begin{pmatrix} a_{1} \\ a_{2} \\ a_{3} \end{pmatrix} \circ \begin{pmatrix} b_{1} \\ b_{2} \\ b_{3} \end{pmatrix} = a_{1}b_{1} + a_{2}b_{2} + a_{3}b_{3}\]
\[\begin{align*} V_{ABCDS} &= \frac{1}{3} \cdot \left| \left( \overrightarrow{AB} \times \overrightarrow{AD} \right) \circ \overrightarrow{AS}\; \right| \\[0.8em] &= \frac{1}{3} \cdot \left| \left[ \begin{pmatrix} 0 \\ 12 \\ 0 \end{pmatrix} \times \begin{pmatrix} -12 \\ 0 \\ 0 \end{pmatrix} \right] \circ \begin{pmatrix} -6 \\ 6 \\ 8 \end{pmatrix} \right| \\[0.8em] &= \frac{1}{3} \cdot \left| \begin{pmatrix} 12 & \cdot & 0 & - & 0 & \cdot & 0 \\ 0 & \cdot & (-12) & - & 0 & \cdot & 0 \\ 0 & \cdot & 0 & - & 12 & \cdot & (-12) \end{pmatrix} \circ \begin{pmatrix} -6 \\ 6 \\ 8 \end{pmatrix} \right| \\[0.8em] &= \frac{1}{3} \cdot \left| \begin{pmatrix} 0 \\ 0 \\ 144 \end{pmatrix} \circ \begin{pmatrix} -6 \\ 6 \\ 8 \end{pmatrix} \right| \\[0.8em] &= \frac{1}{3} \cdot \left| 0 \cdot (-6) + 0 \cdot 6 + 144 \cdot 8 \right| \\[0.8em] &= 384 \end{align*}\]
Das Volumne des Pavillons beträgt 384 m³.

