Der Graph von \(F\) verläuft durch den Punkt \((\ln 2|0{,}5)\). Begründen Sie ohne weitere Rechnung, dass \(F\) keine größeren Werte als \(0{,}5\) annehmen kann und bei \(x = \ln 4\) eine Wendestelle besitzt. Berechnen Sie die \(y\)-Koordinate des zugehörigen Wendepunkts.
(5 BE)
Lösung zu Teilaufgabe 1d
Extrempunkt und Wendepunkt des Graphen einer Stammfunktion
\[F(x) = 2e^{-x} -2e^{-2x}; \; D_{F} = \mathbb R\]
\[(\ln{2}|0{,}5) \in G_{F}\]
Begründung, dass \(F\) keine größeren Werte als \(0{,}5\) annehmen kann
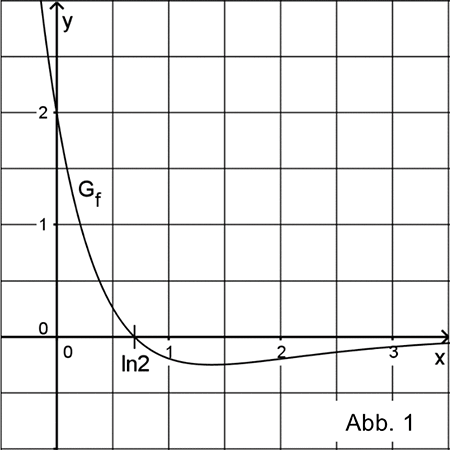
Laut der Angabe zu Aufgabe 1 und Abbildung 1 ist \(x = \ln{2}\) einzige Nullstelle der Funktion \(f\). Zudem zeigt der Verlauf von \(G_{f}\) in Abbildung 1, dass die Funktion \(f\) an der einfachen Nullstelle \(x = \ln{2}\) das Vorzeichen von \(+\) nach \(-\) wechselt.
\[f(\ln{2}) = 0\]
\(f(x) > 0\) für \(x < \ln{2}\)
\(f(x) < 0\) für \(x > \ln{2}\)
Gemäß der Definition einer Stammfunktion gilt:
Stammfunktion
Eine differenzierbare Funktion \(F(x)\) heißt eine Stammfunktion von \(f(x)\), wenn
\(F'(x) = f(x)\) mit \(D_{F} = D_{f}\)
gilt.
\[F'(x) = f(x)\]
Folglich ist \(x = \ln{2}\) einzige Extremstelle der Stammfunktion \(F\) und \(G_{F}\) besitzt den absoluten Hochpunkt \(HoP(\ln{2}|0{,}5)\). Damit kann die Stammfunktion \(F\) keine größeren Werte als \(0{,}5\) annehmen.
Anwendung der Differentialrechnung:
Extrempunkte
Ist \(f'(x_{0}) = 0\) und wechselt \(f'\) an der Stelle \(x_{0}\) das Vorzeichen, so hat \(G_{f}\) an der Stelle \(x_{0}\) einen Extrempunkt.
(vgl. Merkhilfe)
\[\left. \begin{align*} &F'(x) > 0 \; \text{für} \; x < \ln{2} \\[0.8em] &F'(\ln{2}) = 0 \\[0.8em] &F'(x) < 0 \; \text{für} \; x > \ln{2} \end{align*} \right\} \enspace \Rightarrow \enspace \text{absoluter Hochpunkt}\; HoP(\ln{2}|0{,}5)\]
Begründung, dass \(F\) bei \(x = \ln{4}\) eine Wendestelle besitzt
Aus Teilaufgabe 1b ist bekannt, dass \(x = \ln{4}\) die Extremstelle der Funktion \(f\) ist und \(G_{f}\) den Tiefpunkt \(TiP\Big( \ln{4} \Big| -\frac{1}{4}\Big)\) hat. Abbildung 1 bestätigt dieses Ergebnis.
Zudem wurde durch den Nachweis des Tiefpunkts in Teilaufgabe 1b gezeigt, dass \(f'(x) < 0\) für \(x < \ln{4}\) und \(f'(x) > 0\) für \(x > \ln{4}\) gilt.
Stammfunktion
Eine differenzierbare Funktion \(F(x)\) heißt eine Stammfunktion von \(f(x)\), wenn
\(F'(x) = f(x)\) mit \(D_{F} = D_{f}\)
gilt.
Mit \(F''(x) = f'(x)\) folgt daraus, dass die Stammfunktion \(F\) bei \(x = \ln{4}\) eine Wendestelle besitzt.
Anwendung der Differetialrechnung:
Wendepunkt
Ist \(f''(x_0) = 0\) und wechselt \(f''\) an der Stelle \(x_0\) das Vorzeichen, so hat \(G_f\) an der Stelle \(x_0\) einen Wendepunkt.
(vgl. Merkhilfe)
Alternative:
Es muss \(f''(x_{0}) = 0\) und \(f'''(x_{0}) \neq 0\) gelten.
\[\left. \begin{align*} &F''(x) < 0 \; \text{für} \; x < \ln{4} \\[0.8em] &F''(\ln{4}) = 0 \\[0.8em] &F''(x) > 0 \; \text{für} \; x > \ln{4} \end{align*} \right\} \enspace \Rightarrow \enspace \text{Wendepunkt}\; W(\ln{4}|F(\ln{4}))\]
\(y\)-Koordinate des Wendepunkts von \(G_{F}\)
Die Stelle \(x = \ln{4}\) ist Wendestelle der Stammfunktion \(F\). Folglich hat der Wendepunkt des Graphen \(G_{F}\) die Koordinaten \(W(\ln{4}|F(\ln{4}))\).
\[F(x) = 2e^{-x} -2e^{-2x}; \; D_{F} = \mathbb R\]
\[\begin{align*} F(\ln{4}) &= 2e^{-\ln{4}} - 2e^{-2\ln{4}} & &| \; n \cdot \log_{a}{b} = \log_{a}\left( b^{n} \right) \\[0.8em] &= 2e^{\ln\big( 4^{-1} \big)} - 2e^{\ln\big( 4^{-2} \big)} & &| \; a^{-n} = \frac{1}{a^{n}} \\[0.8em] &= 2e^{\left( \frac{1}{4} \right)} - 2e^{\ln\left( \frac{1}{4^{2}} \right)} & &| \; e^{\ln{x}} = x \; \left( \text{allg.:} \; a^{\log_{a}{x}} = x \right) \\[0.8em] &= 2 \cdot \frac{1}{4} - 2 \cdot \frac{1}{16} \\[0.8em] &= \frac{1}{2} - \frac{1}{8} \\[0.8em] &= \frac{3}{8} \end{align*}\]
\[\Longrightarrow \quad W \left( \ln{4} \bigg| \frac{3}{8} \right)\]
