Die Punkte \(M\) und \(P\) sind die Mittelpunkte der Kanten \([AD]\) bzw. \([BC]\). Der Punkt \(K\,(0|y_K|4)\) liegt auf der Kante \([DF]\). Bestimmen Sie \(y_K\) so, dass das Dreieck \(KMP\) in \(M\) rechtwinklig ist.
(3 BE)
Lösung zu Teilaufgabe 1b
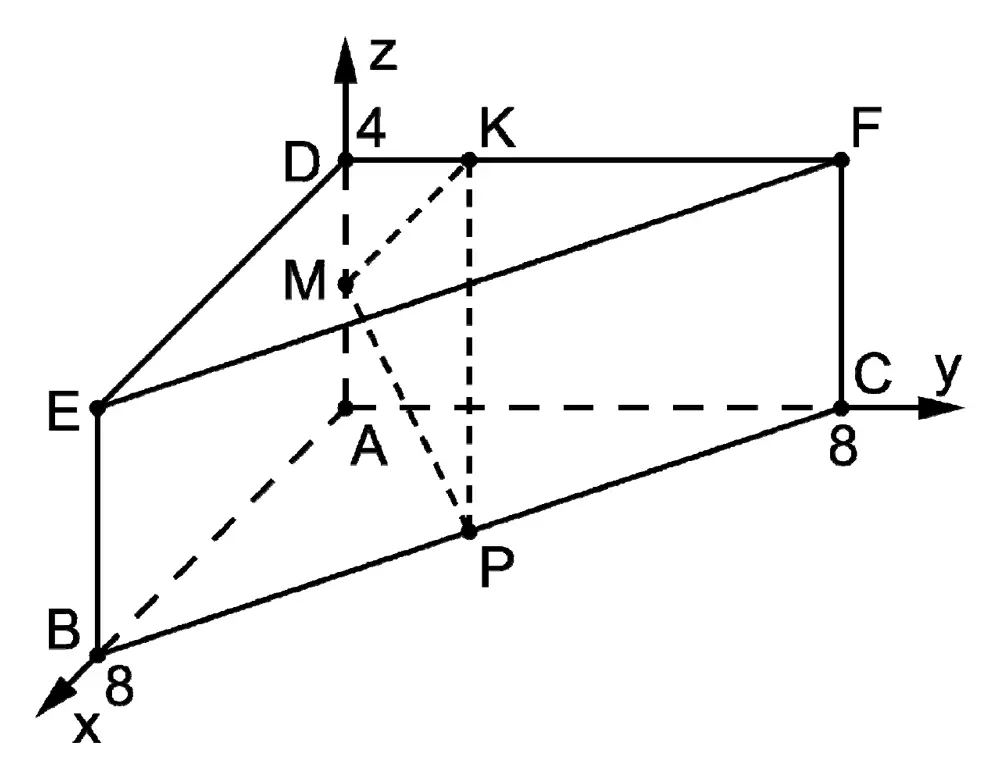
Das Dreieck \(KMP\) ist in \(M\) rechtwinklig, wenn die Strecken \([MK]\) und \([MP]\) bzw. die Vektoren \(\overrightarrow{MK}\) und \(\overrightarrow{MP}\) zueinander senkrecht sind.
Anwendung des Skalarprodukts:
Orthogonale (zueinander senkrechte) Vektoren (vgl. Merkhilfe)
\[\overrightarrow{a} \perp \overrightarrow{b} \; \Leftrightarrow \; \overrightarrow{a} \circ \overrightarrow{b} \quad (\overrightarrow{a} \neq \overrightarrow{0},\; \overrightarrow{b} \neq \overrightarrow{0})\]
\[\overrightarrow{MK} \perp \overrightarrow{MP} \quad \Longleftrightarrow \quad \overrightarrow{MK} \circ \overrightarrow{MP} = 0\]
Vektoren \(\overrightarrow{M}\) und \(\overrightarrow{P}\) berechnen:
Mittelpunkt einer Strecke
Für den Ortsvektor \(\overrightarrow{M}\) des Mittelpunkts \(M\) einer Strecke \([AB]\) gilt:
\[\overrightarrow{M} = \frac{1}{2} \left( \overrightarrow{A} + \overrightarrow{B} \right)\]
\[\overrightarrow{M} = \frac{1}{2} \cdot \left( \overrightarrow{A} + \overrightarrow{D}\right) = \frac{1}{2} \cdot \overrightarrow{D} = \frac{1}{2} \cdot \begin{pmatrix} 0 \\ 0 \\ 4 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ 2 \end{pmatrix}\]
\[\overrightarrow{P} = \frac{1}{2} \cdot \left( \overrightarrow{B} + \overrightarrow{C}\right) = \frac{1}{2} \cdot \left[ \begin{pmatrix} 8 \\ 0 \\ 0 \end{pmatrix} + \begin{pmatrix} 0 \\ 8 \\ 0 \end{pmatrix} \right] = \frac{1}{2} \cdot \begin{pmatrix} 8 \\ 8 \\ 0 \end{pmatrix} = \begin{pmatrix} 4 \\ 4 \\ 0 \end{pmatrix}\]
Koordinate \(y_{K}\) berechnen:
Skalarprodukt
Unter dem Skalarprodukt \(\overrightarrow{a} \circ \overrightarrow{b}\) zweier Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) versteht man das Produkt aus den Beträgen der beiden Vektoren und dem Kosinus des von den Vektoren eingeschlossenen Winkels \(\varphi\).
\[\overrightarrow{a} \circ \overrightarrow{b} = \vert \overrightarrow{a} \vert \cdot \vert \overrightarrow{b} \vert \cdot \cos{\varphi} \quad (0^{\circ} \leq \varphi \leq 180^{\circ})\]
Berechnung eines Skalarprodukts im \(\boldsymbol{\mathbb R^{3}}\) (vgl. Merkhilfe)
\[\overrightarrow{a} \circ \overrightarrow{b} = \begin{pmatrix} a_{1} \\ a_{2} \\ a_{3} \end{pmatrix} \circ \begin{pmatrix} b_{1} \\ b_{2} \\ b_{3} \end{pmatrix} = a_{1}b_{1} + a_{2}b_{2} + a_{3}b_{3}\]
\[\begin{align*} \overrightarrow{MK} \circ \overrightarrow{MP} &= 0 \\[0.8em] (\overrightarrow{K} - \overrightarrow{M}) \circ (\overrightarrow{P} - \overrightarrow{M}) &= 0 \\[0.8em] \left[ \begin{pmatrix} 0 \\ y_{K} \\ 4 \end{pmatrix} - \begin{pmatrix} 0 \\ 0 \\ 2 \end{pmatrix} \right] \circ \left[ \begin{pmatrix} 4 \\ 4 \\ 0 \end{pmatrix} - \begin{pmatrix} 0 \\ 0 \\ 2 \end{pmatrix} \right] &= 0 \\[0.8em] \begin{pmatrix} 0 \\ y_{K} \\ 2 \end{pmatrix} \circ \begin{pmatrix} 4 \\ 4 \\ -2 \end{pmatrix} &= 0 \\[0.8em] 0 \cdot 4 + y_{K} \cdot 4 + 2 \cdot (-2) &= 0 \\[0.8em] 4y_{K} - 4 &= 0 & &| +4 \\[0.8em] 4y_{K} &= 4 & &| : 4 \\[0.8em] y_{K} &= 1 \end{align*}\]
\[\Longrightarrow \quad K\,(0|1|4)\]
Das Dreieck \(KMP\) ist für \(y_{K} = 1\) in \(M\) rechtwinklig.
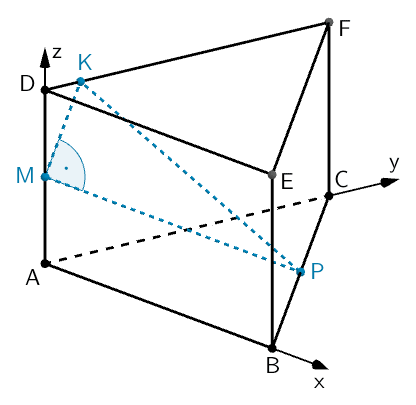
Gerades Prisma \(ABCDEF\), rechtwinkliges Dreieck \(KMP\)


