Abiturlösungen Mathematik Bayern 2017 Prüfungsteil A Stochastik 2
Nebenstehende Vierfeldertafel gehört zu einem Zufallsexperiment mit den stochastisch unabhängigen Ereignissen \(A\) und \(B\). Tragen Sie alle fehlenden Wahrscheinlichkeiten ein.
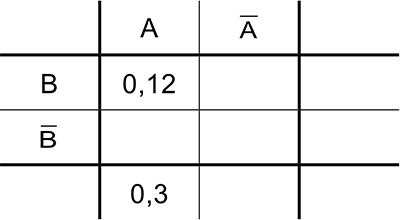
(3 BE)
- Details
- Hauptkategorie: Prüfungsteil A
Im Vorfeld einer Wahl wird eine wahlberechtigte Person zufällig ausgewählt und befragt. Betrachtet werden folgende Ereignisse:
\(C\): „Die Person ist älter als 50 Jahre."
\(D\): „Die Person will die derzeitige Regierungspartei wählen."
Erläutern Sie, was in diesem Sachzusammenhang eine stochastische Unabhängigkeit der Ereignisse \(C\) und \(D\) bedeuten würde.
(2 BE)
- Details
- Hauptkategorie: Prüfungsteil A
Schwarze und weiße Kugeln sind wie folgt auf drei Urnen verteilt:
Aus Urne A wird zunächst eine Kugel zufällig entnommen und in Urne B gelegt. Anschließend wird aus Urne B eine Kugel zufällig entnommen und in Urne C gelegt. Bestimmen Sie die Wahrscheinlichkeit dafür, dass sich danach in Urne C zwei weiße Kugeln und eine schwarze Kugel befinden.
(2 BE)
- Details
- Hauptkategorie: Prüfungsteil A
Die drei Urnen mit den in der Abbildung dargestellten Inhalten bilden den Ausgangspunkt für folgendes Spiel:
Es wird zunächst ein Einsatz von 1 € eingezahlt. Anschließend wird eine der drei Urnen zufällig ausgewählt und danach aus dieser Urne eine Kugel zufällig gezogen. Nur dann, wenn diese Kugel schwarz ist, wird ein bestimmter Geldbetrag ausgezahlt.
Ermitteln Sie, wie groß dieser Geldbetrag sein muss, damit bei diesem Spiel auf lange Sicht Einsätze und Auszahlungen ausgeglichen sind.
(3 BE)
- Details
- Hauptkategorie: Prüfungsteil A
2023 Christian Rieger・mathelike
