Das Volumen des Wassers im Aquarium lässt sich analog zum Rauminhalt eines Prismas mit Grundfläche \(G\) und Höhe \(h\) berechnen. Erläutern Sie, dass der Term \(\displaystyle 24 \cdot \int_{0{,}2}^{4} \left( f(0{,}2) - f(x) \right) dx\) das Wasservolumen im vollgefüllten Aquarium in Kubikmetern beschreibt.
(3 BE)
Lösung zu Teilaufgabe 2e
Volumen eines Prismas: \(V = G \cdot h\)
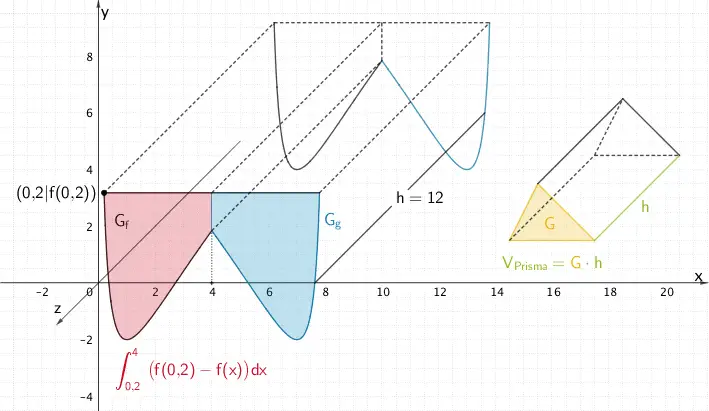
Das Integral \(\displaystyle \textcolor{#cc071e}{\int_{0{,}2}^{4} \left( f(0{,}2) - f(x) \right)dx}\) errechnet die Maßzahl des Inhalts des Flächenstücks, welches die Gerade \(y = f(0{,}2)\) (vorderer oberer Beckenrand) und \(G_{f}\) im Intervall \([0{,}2;4]\) einschließen. Das Doppelte dieses Flächeninhalts entspricht der Grundfläche \(G\) eines Prismas. Die Länge 12 m des Aquariums entspricht der Höhe \(h\) eines Prismas.
\[G = 2 \cdot \textcolor{#cc071e}{\int_{0{,}2}^{4} \left( f(0{,}2) - f(x) \right)dx}; \; h = 12\]
\[\begin{align*}V &= G \cdot h \\[0.8em] &= 2 \cdot \int_{0{,}2}^{4} \left( f(0{,}2) - f(x) \right)dx \cdot 12 \\[0.8em] &= 24 \cdot \int_{0{,}2}^{4} \left( f(0{,}2) - f(x) \right)dx \end{align*}\]
Da eine Längeneinheit im Koordinatensystem einem Meter in der Realität entspricht (vgl. Angabe), hat die Grundfläche \(G\) die Einheit Quadratmeter. Die Höhe \(h\) beträgt 12 Meter (vgl. Angabe). Also beschreibt der Term \(\displaystyle 24 \cdot \int_{0{,}2}^{4} \left( f(0{,}2) - f(x) \right) dx\) das Wasservolumen des vollgefüllten Aquariums in Kubikmetern.


