Für eine Quizshow sucht ein Fernsehsender Abiturientinnen und Abiturienten als Kandidaten. Jeder Bewerber gibt in einem online auszufüllenden Formular die Duchschnittsnote seines Abiturzeugnisses an.
Insgesamt bewerben sich dreimal so viele weibliche wie männliche Personen, wobei 80 % der weiblichen und 75 % der männlichen Bewerber eine Durchschnittsnote von 1,5 oder besser angeben. Bestimmen Sie den Anteil der Personen unter allen Bewerbern, die eine schlechtere Durchschnittsnote als 1,5 angeben.
(4 BE)
Lösung zu Teilaufgabe 1
Ereignisse festlegen:
\(W\,\): weiblicher Bewerber
\(M\,\): männlicher Bewerber
\(D\,\): Berwerber gibt Duchschnittsnote 1,5 oder besser an
\(\overline{D}\,\): Bewerber gibt schlechtere Duchschnittsnote als 1,5 an
Analyse der Angabe:
"... bewerben sich dreimal so viele weibliche wie männliche Personen, ..."
\[\Longrightarrow \quad \vert W \vert = 3 \cdot \vert M \vert\]
"... wobei 80 % der weiblichen ... Bewerber eine Durchschnittsnote von 1,5 oder besser angeben."
\[\Longrightarrow \quad P_W(D) = 0{,}8\]
Bedingte Wahrscheinlichkeit
Die Wahrscheinlichkeit für das Eintreten des Ereignisses \(B\) unter der Voraussetzung oder der Bedingung, dass das Ereignis \(A\) bereits eingetreten ist, heißt bedingte Wahrscheinlichkeit von \(\boldsymbol{B}\) unter der Bedingung \(\boldsymbol{A}\) und wird durch die Schreibweise \(P_{A}(B)\) gekennzeichnet.
Es gilt: \(P_{A}(B) = \dfrac{P(A \cap B)}{P(A)} \quad (P(A) \neq 0)\)
(vgl. Merkhilfe)
"... wobei 75 % der männlichen Bewerber eine Durchschnittsnote von 1,5 oder besser angeben."
\[\Longrightarrow \quad P_M(D) = 0{,}75\]
1. Lösungsansatz: Baumdiagramm
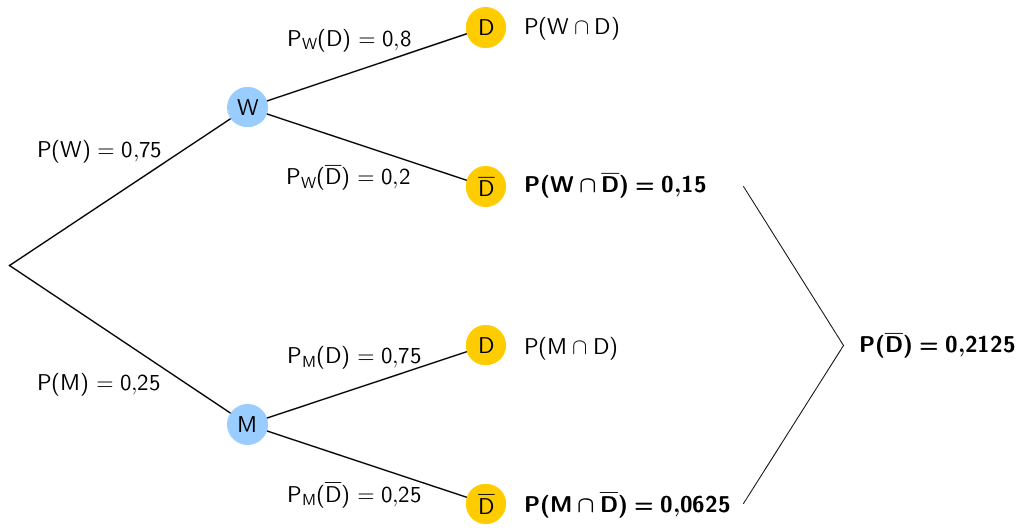
Pfadregeln
Verzweigungsregel (Knotenregel)
Die Summe der Wahrscheinlichkeiten an den Ästen, die von einem Knoten ausgehen, ist gleich eins.
1. Pfadregel (Produktregel)
Die Wahrscheinlichkeit eines Ergebnisses ist gleich dem Produkt der Wahrscheinlichkeiten entlang des Pfades, der zu dem Ergebnis führt.
2. Pfadregel (Summenregel)
Die Wahrscheinlichkeit eines Ereignisses ist gleich der Summe der Wahrscheinlichkeiten der Ergebnisse, die zu diesem Ereignis gehören.
Anwenden der Knotenregel:
\[\left. \begin{align*} \vert W \vert = 3 \cdot \vert M \vert \\[0.8em] P(W) + P(M) = 1 \end{align*} \right\} \Longrightarrow \quad P(W) = 0{,}75\,; \enspace P(M) = 0{,}25\]
\[\begin{align*} P_W(D) + P_W(\overline{D}) &= 1 \\[0.8em] P_W(\overline{D}) &= 1 - P_W(D) = 1 - 0{,}8 = 0{,}2 \end{align*}\]
\[\begin{align*} P_M(D) + P_M(\overline{D}) &= 1 \\[0.8em] P_M(\overline{D}) &= 1 - P_M(D) = 1 - 0{,}75 = 0{,}25 \end{align*}\]
Anwenden der 1. Pfadregel:
\[\begin{align*} P(W \cap \overline{D}) &= P(W) \cdot P_W(\overline{D}) \\[0.8em] &= 0{,}75 \cdot 0{,}2 \\[0.8em] &= 0{,}15 \end{align*}\]
\[\begin{align*} P(M \cap \overline{D}) &= P(M) \cdot P_M(\overline{D}) \\[0.8em] &= 0{,}25 \cdot 0{,}25 \\[0.8em] &= 0{,}0625 \end{align*}\]
Anwenden der 2. Pfadregel:
\[\begin{align*} P(\overline{D}) &= P(W \cap \overline{D}) + P(M \cap \overline{D}) \\[0.8em] &= 0{,}15 + 0{,}0625 \\[0.8em] &= 0{,}2125 = 21{,}25\,\% \end{align*}\]
2.Lösungsansatz: Vierfeldertafel der Wahrscheinlichkeiten
Gegeben:
\[P(W) = 0{,}75 \hspace{50px} P_W(D) = 0{,}8\]
\[P(M) = 0{,}25 \hspace{50px} P_M(D) = 0{,}75\]
\(P(\overline{D})\,\) mithilfe der Vierfeldertafel berechnen:
| \(D\) | \(\overline D\) | ||
| \(W\) | \(0{,}8 \cdot 0{,}75\) | \(\bf{0{,}15}\) | \(0{,}75\) |
| \(M\) | \(0{,}75 \cdot 0{,}25\) | \(\bf{0{,}0625}\) | \(0{,}25\) |
| \(\bf{0{,}2125}\) | \(1\) |
\[\begin{align*} P(W \cap \overline{D}) &= P(W) - P(W \cap D) \\[0.8em] &= 0{,}75 - 0{,}8 \cdot 0{,}75 \\[0.8em] &= 0{,}15 \end{align*}\]
\[\begin{align*} P(M \cap \overline{D}) &= P(M) - P(M \cap D) \\[0.8em] &= 0{,}25 - 0{,}75 \cdot 0{,}25 \\[0.8em] &= 0{,}0625 \end{align*}\]
\[\begin{align*} P(\overline{D}) &= P(W \cap \overline{D}) + P(M \cap \overline{D}) \\[0.8em] &= 0{,}15 + 0{,}0625 \\[0.8em] &= 0{,}2125 = 21{,}25\,\% \end{align*}\]

