Geben Sie \(g'(0)\) an un zeichnen Sie \(G_{g}\) im Bereich \(-4 \leq x \leq 4\) unter Berücksichtigung der bisherigen Ergebnisse und der Tatsache, dass \(G_{g}\) in \(W(0|g(0))\) seinen einzigen Wendepunkt hat, in ein Koordinatensystem ein.
(3 BE)
Lösung zu Teilaufgabe 2b
\[g(x) = \frac{e^{x}}{e^{x} + 1}; \; D_{g} = \mathbb R\]
\(g'(x) = \dfrac{e^{x}}{(e^{x} + 1)^{2}}\) (vgl. Teilaufgabe 2a)
Funktionswert \(g'(0)\)
\(g'(0)\) beschreibt die Steigung der Wendetangente im Wendepunkt \(W(0|g(0))\) (vgl. Angabe).
Anwendung der Differetialrechnung:
Steigung \(m_{T}\) einer Tangente \(T\) an den Graphen einer Funktion \(f\) im Punkt \(P\,(\,x_0\,|\,f(x_0)\,)\)
\[m_{T} = f'(x_0)\]
(vgl. Merkhilfe)
\[g'(\textcolor{#e9b509}{0}) = \frac{e^{\textcolor{#e9b509}{0}}}{(e^{\textcolor{#e9b509}{0}} + 1)^{2}} = \frac{1}{(1 + 1)^{2}}= \frac{1}{4}\]
Zeichnung von \(G_{g}\)
Bisherige Ergebnisse und Informationen:
- \(g\) ist in \(\mathbb R\) streng monoton zunehmend (vgl. Teilaufgabe 2a).
- \(g\) besitzt die Wertemenge \(]0;1[\,\)(vgl. Teilaufgabe 2a).
- \(W(0|g(0))\) ist einziger Wendepunkt von \(G_{g}\) mit \(g(0) = \dfrac{e^{0}}{e^{0} + 1} = \dfrac{1}{1 + 1}= \dfrac{1}{2}\).
- Steigung der Wendetangente: \(g'(0) = \textcolor{#cc071e}{\dfrac{1}{4}}\)
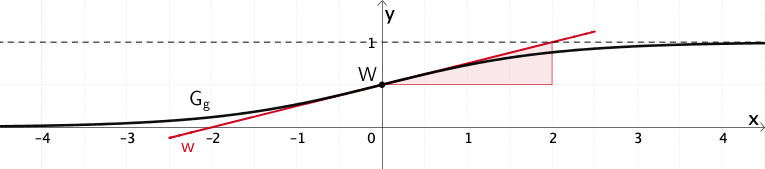
Graph der Funktion \(g\) mit Wendepunkt \(W\) und Wendetangente \(\textcolor{#cc071e}{w}\) (optional)

