Achsensymmetrie bzgl. der \(y\)-Achse
Der Graph einer Funktion \(f\) verläuft achsensymmetrisch zur \(y\)-Achse, wenn \(f(-x) = f(x)\) gilt.
Achsensymmetrie von \(\boldsymbol{G_{f}}\) bzgl. der \(\boldsymbol{y}\)-Achse
\[f(-x) = f(x)\]
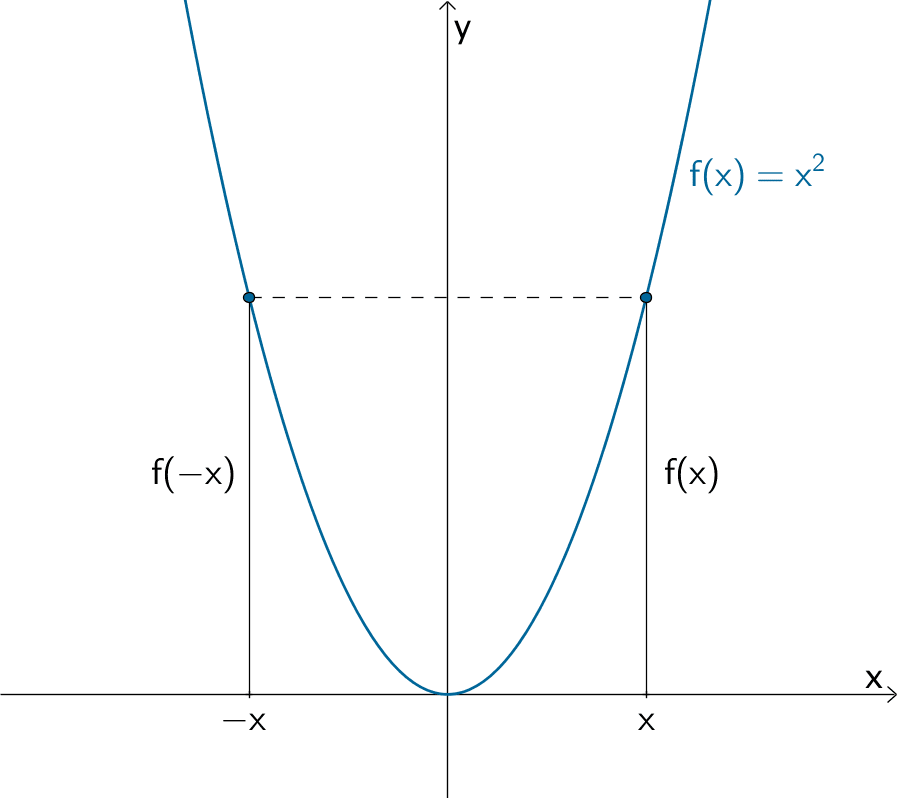
Normalparabel der Funktion \(f \colon x \mapsto x^{2}\)
Punktsymmetrie bzgl. des Ursprungs \(O(0|0)\)
Der Graph einer Funktion \(f\) verläuft punktsymmetrisch zum Ursprung, wenn \(f(-x) = -f(x)\) gilt.
Punktsymmetrie von \(\boldsymbol{G_{f}}\) bzgl. des Koordinatenursprungs \(\boldsymbol{O(0|0)}\)
\[f(-x) = -f(x)\]
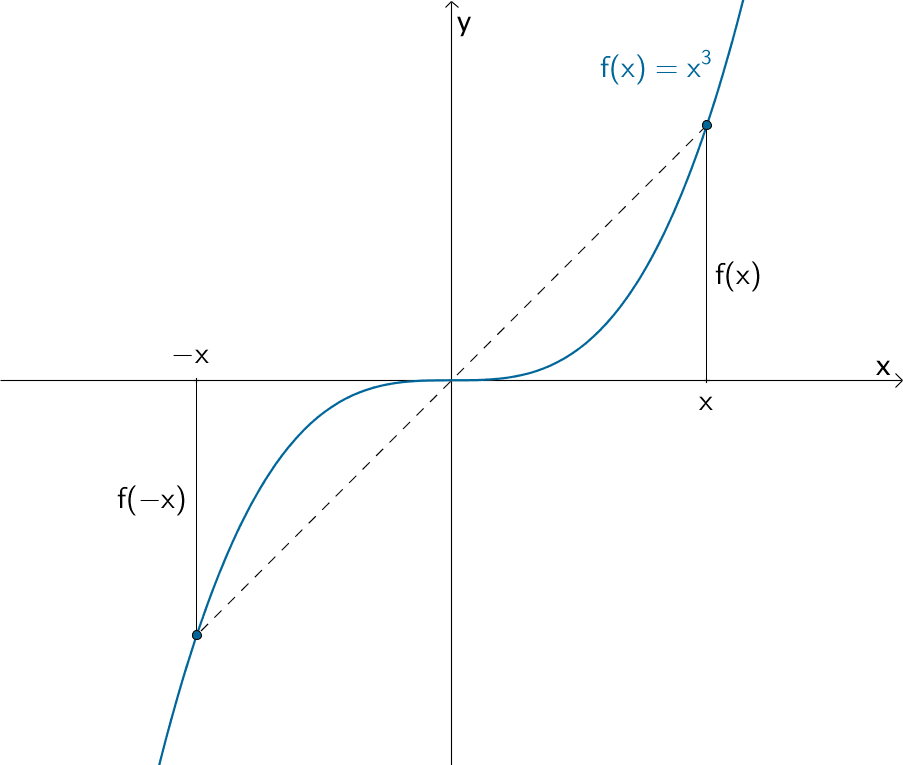
Graph der kubischen Funktion \(f\colon x \mapsto x^{3}\)
Beispielaufgabe
Gegeben sei die in \(\mathbb R\) definierte Funktion \(f \colon x \mapsto x^{2} \cdot \sin x\). Überprüfen Sie rechnerisch das Symmetrieverhalten des Graphen der Funktion \(f\) bzgl. des Koordinatensystems.
\[f(x) = x^{2} \cdot \sin x; \; D = \mathbb R\]
\[\begin{align*}f(-x) &= (-x)^{2} \cdot \sin {(-x)} & &| \; \sin {(-x)} = - \sin x \\[0.8em] &= -x^{2} \cdot \sin x \\[0.8em] &= -f(x) \end{align*}\]
\(\Longrightarrow \quad\)Der Graph der Funktion \(f\) ist punktsymmetrisch zum Ursprung.
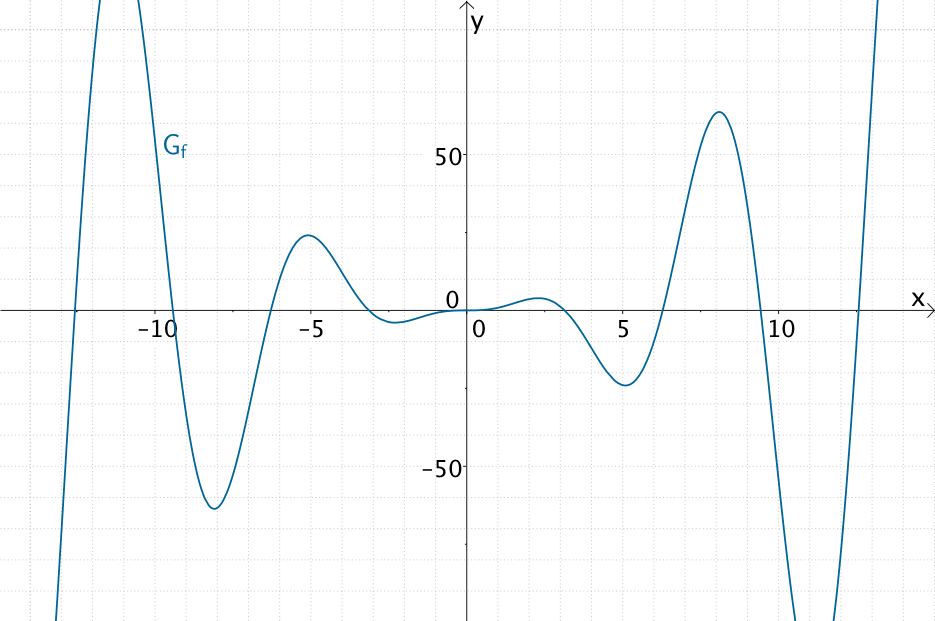
Graph der Funktion \(f \colon x \mapsto x^{2} \cdot \sin x\)


