Durch Spiegelung von \(G_{f}\) an der Geraden \(x = 4\) entsteht der Graph einer in \(]-\infty;8[\) definierten Funktion \(g\). Dieser Graph wird mit \(G_{g}\) bezeichnet.
Zeichnen Sie \(G_{g}\) in Abbildung 1 ein.
(2 BE)
Lösung zu Teilaufgabe 2a
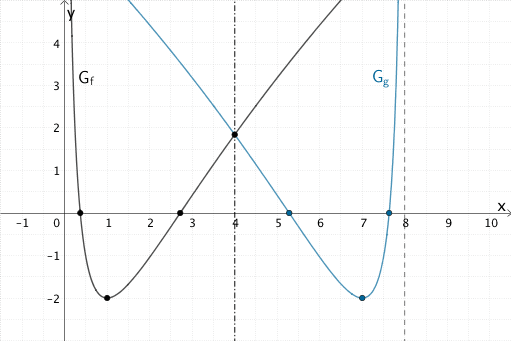
Für die Zeichnung von \(G_{g}\) empfiehlt sich die Spiegelung der bekannten Nullstellen und des Tiefpunkts von \(G_{f}\) sowie die Berücksichtigung des Fixpunktes \((4|f(4))\) auf der Spiegelachse. Die senkrechte Asymptote von \(G_{g}\) ergibt sich durch Spiegelung der \(y\)-Achse (senkrechte Asymptote von \(G_{f}\)).


