Gegeben sind die Punkte \(A(2|1|-4)\), \(B(6|1|-12)\) und \(C(0|1|0)\).
Weisen Sie nach, dass der Punkt \(C\) auf der Geraden \(AB\), nicht aber auf der Strecke \([AB]\) liegt.
(3 BE)
Lösung zu Teilaufgabe 1a
Geradengleichung in Parameterform, Punktprobe
Gleichung einer Gerade / Strecke in Parameterform
Jede Gerade \(g\) kann durch eine Gleichung in der sogenannten Parameterform
\(g \colon \overrightarrow{X} = \overrightarrow{A} + \lambda \cdot \overrightarrow{u} \enspace\) mit dem Parameter \(\lambda \in \mathbb R\) beschrieben werden.
Dabei ist \(\overrightarrow{A}\) der Ortsvektor eines Aufpunkts (Stützvektor) und \(\overrightarrow{u}\) ein Richtungsvektor der Gerade \(g\).
Gleichung einer Strecke \([AB]\) in Parameterform:
\[\overrightarrow{X} = \overrightarrow{A} + \lambda \cdot \overrightarrow{AB}, \; \textcolor{#cc071e}{\lambda \in [0;1]} \]
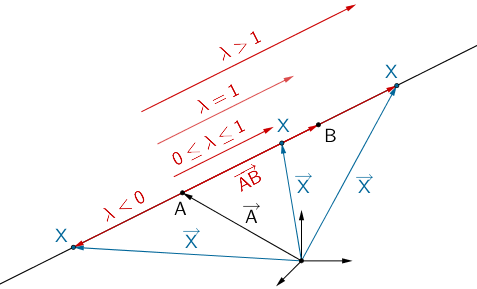
Lage eines beliebigen Punktes \(X\) einer Geraden \(AB\) durch die Punkte \(A\) und \(B\) in Abhängigkeit des Werts des Parameters \(\lambda\).
Der Punkt \(C\) liegt auf der Geraden \(AB\), wenn der Ortsvektor \(\overrightarrow{C}\) die Gleichung der Geraden \(AB\) in Parameterform erfüllt (Punktprobe). Der Punkte \(C\) liegt für \(0 < \lambda < 1\) auf der Strecke \([AB]\). Für \(\lambda < 0\) oder \(\lambda > 1\) liegt der Punkt \(C\) nicht auf der Strecke \([AB]\).
Gleichung der Geraden \(AB\) in Parameterform:
Beispielsweise wird der Ortsvektor \(\overrightarrow{A}\) als Stützvektor und der Verbindungsvektor \(\overrightarrow{AB}\) als Richtungsvektor der Gleichung der Geraden \(AB\) gewählt.
Gleichung einer Gerade / Strecke in Parameterform
Jede Gerade \(g\) kann durch eine Gleichung in der sogenannten Parameterform
\(g \colon \overrightarrow{X} = \overrightarrow{A} + \lambda \cdot \overrightarrow{u} \enspace\) mit dem Parameter \(\lambda \in \mathbb R\) beschrieben werden.
Dabei ist \(\overrightarrow{A}\) der Ortsvektor eines Aufpunkts (Stützvektor) und \(\overrightarrow{u}\) ein Richtungsvektor der Gerade \(g\).
Gleichung einer Strecke \([AB]\) in Parameterform:
\[\overrightarrow{X} = \overrightarrow{A} + \lambda \cdot \overrightarrow{AB}, \; \textcolor{#cc071e}{\lambda \in [0;1]} \]
\[AB \colon \overrightarrow{X} = \overrightarrow{A} + \lambda \cdot \overrightarrow{AB}; \; \lambda \in \mathbb R\]
Verbindungsvektor \(\overrightarrow{AB}\) berechnen:
\(A(2|1|-4)\), \(B(6|1|-12)\)
\[\overrightarrow{AB} = \overrightarrow{B} - \overrightarrow{A} = \begin{pmatrix} 6 \\ 1 \\ -12 \end{pmatrix} - \begin{pmatrix} 2 \\ 1 \\ -4 \end{pmatrix} = \begin{pmatrix} 4 \\ 0 \\ -8 \end{pmatrix}\]
Gleichung der Geraden \(AB\) formulieren:
\[AB \colon \overrightarrow{X} = \begin{pmatrix} 2 \\ 1 \\ -4 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 4 \\ 0 \\ -8 \end{pmatrix}; \; \lambda \in \mathbb R\]
Punktprobe \(C \in AB\):
\(C(0|1|0)\)
\[C \in AB \colon \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix} = \begin{pmatrix} 2 \\ 1 \\ -4 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 4 \\ 0 \\ -8 \end{pmatrix}\]
Liest man die Vektorgleichung koordinatenweise (zeilenweise), ergibt sich folgendes lineare Gleichungssystem:
\[\Longrightarrow \enspace \begin{cases} 0 = 2 + 4\lambda \quad \; \Longrightarrow \enspace \lambda = -\frac{1}{2} \\[0.8em] 1 = 1 \\[0.8em] 0 = -4 - 8\lambda \enspace \Longrightarrow \enspace \lambda = -\frac{1}{2} \end{cases}\]
Das Gleichungssystem hat die eindeutigen Lösung \(\lambda = -\frac{1}{2}\) und es gilt somit \(\lambda < 0\). Folglich liegt der Punkt \(C\) auf der Geraden \(AB\), nicht aber auf der Strecke \([AB]\).


