Eine Funktion \(f\) mit \(\displaystyle f(x) = \sqrt[n]{x} = x^{\frac{1}{n}}\) und \(n \in \mathbb N\) heißt Wurzelfunktion. Der mathematische Ausdruck unter dem Wurzelzeichen heißt Radikand und \(n\) heißt Wurzelexponent. Der Wert des Radikanden muss stets größer oder gleich Null sein.
Definitionsbereich: \(D_{f} = \mathbb R^{+}_{0}\)
Wertebereich: \(W_{f} = \mathbb R^{+}_{0}\)
Eigenschaften der Wurzelfunktion
Einzige Nullstelle: \(x = 0\)
Der Graph einer Wurzelfunktion \(f\) verläuft für \(n \in \mathbb N\) im I. Quadranten durch den Punkt \((1|1) \; (\sqrt[n]{1} = 1\)) und ist streng monoton steigend.
Der Graph einer Wurzelfunktion \(f\) mündet an der Stelle \(x = 0\) senkrecht zur \(x\)-Achse. Dieses Verhalten ist umso ausgeprägter, je größer \(n\) ist. Die Steigung der Tangente an den Graphen einer Wurzelfunktion geht an der Stelle \(x = 0\) gegen \(+\infty\).
Beispiel Quadratwurzel:
\(\lim \limits_{x\, \to \, 0^{+}} \left( \sqrt{x} \right)' = \lim \limits_{x\,\to\,0^{+}} \dfrac{1}{2\sqrt{x}} = +\infty\) (vgl. Abiturskript - 1.5.2 Ableitungsregeln).
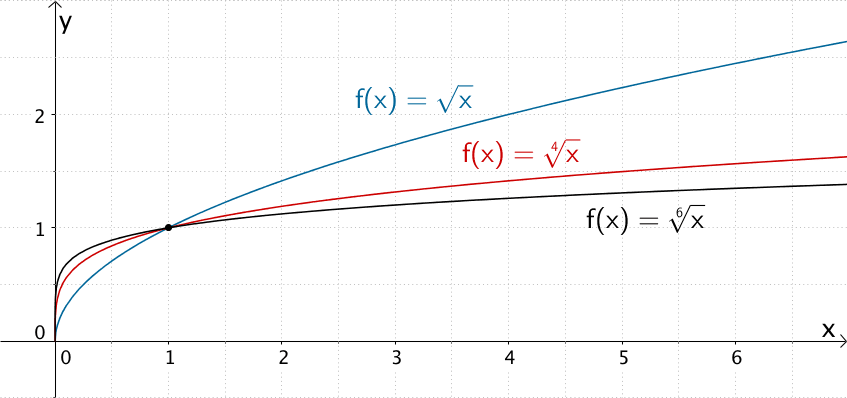
Graphen der Wurzelfunktionen \(f\colon x\mapsto \sqrt{x}\), \(f\colon x\mapsto \sqrt[4]{x}\) und \(f\colon x\mapsto \sqrt[6]{x}\)
Wurzelgleichungen
Bei Wurzelgleichungen tritt die unbekannte Größe (Variable) innerhalb von Wurzelausdrücken auf. Wurzelgleichungen lassen sich im Allgemeinen nicht durch äquivalente Umformungen lösen.
Anmerkung:
Eine äquivalente Umformung lässt die Lösungsmenge einer Gleichung unverändert (z.B. Addition, Subtraktion). Nicht äquivalenten Umformungen (z.B. Quadrieren, ) können zu einer Veränderung der Lösungsmenge führen. Das heißt, es können „Scheinlösungen" auftreten, welche durch eine Vorbetrachtung der möglichen Lösungen oder durch eine Probe aller Lösungen auszuschließen sind.
Im Folgenden werden ausschließlich Wurzelgleichungen betrachtet, bei denen die unbekannte Größe im Radikanden einer Quadratwurzel auftritt.
Beispiel:
\[\sqrt{4x + 2} - 3x + 6 = 0\]
Der Wurzelausdruck wird zunächst isoliert, um diesen in einem zweiten Schritt durch Quadrieren der Gleichung zu beseitigen.
\[\begin{align*}\sqrt{4x + 2} - 3x + 6 &= 0 & &| + 3x - 6 \; \text{(Wurzel isolieren)} \\[0.8em] \sqrt{4x + 2} &= 3x - 6\end{align*}\]
Das Quadrieren der Gleichung ist keine äquivalent Umformung. Deshalb erfolgt vorab eine Betrachtung der möglichen Lösungen der Gleichung.
1. Bedingung: Der Radikand der Wurzel darf nicht negativ werden.
2. Bedingung: Eine Quadratwurzel ist stets größer oder gleich Null. Folglich muss auch der Term \(3x - 6\) größer oder gleich Null sein.
1. Bedingung
\[\begin{align*} 4x + 2 &\geq 0 & &| - 2 \\[0.8em] 4x &\geq -2 & &| : 4 \\[0.8em] x &\geq - \frac{1}{2} \end{align*}\]
2. Bedingung
\[\begin{align*} 3x - 6 &\geq 0 & &| + 6 \\[0.8em] 3x \geq 6 & &| : 3 \\[0.8em] x \geq 2 \end{align*}\]
Beide Bedingungen müssen gleichzeitig erfüllt sein, sodass nur Lösungen aus dem Intervall \(x \geq 2\) in Frage kommen. Treten im Verlauf des weiteren Lösungsverfahrens Werte \(x < 2\) auf, handelt es sich um „Scheinlösungen".
Wurzelausdruck durch Quadrieren beseitigen:
\[\begin{align*}\sqrt{4x + 2} &= 3x - 6 & &| \; (\dots)^{2} \; \text{(Gleichung quadrieren)} \\[0.8em] 4x + 2 &= \underbrace{(3x - 6)^{2}}_{\large{(a\,-\,b)^{2}}} & &| \; \text{2. Binomische Formel} \\[0.8em] 4x + 2 &= \underbrace{9x^{2} - 36x + 36}_{\large{a^{2}\,-\,2ab\,+\,b^{2}}}\end{align*}\]
Quadratische Gleichung formulieren und Lösungsformel für quadratische Gleichungen anwenden (vgl. Abiturskript - 1.1.2 Quadratische Funktion, Lösungsformel für quadratische Gleichungen, vgl. Merkhilfe):
\[\begin{align*} 4x + 2 &= 9x^{2} - 36x + 36 & &| - 4x - 2 \\[0.8em] 0 &= 9x^{2} - 40x + 34 \end{align*}\]
\[\begin{align*}x_{1,2} &= \frac{40 \pm \sqrt{40^{2} - 4 \cdot 9 \cdot 34}}{2 \cdot 9} \\[0.8em] &= \frac{40 \pm \sqrt{376}}{18} \\[0.8em] &= \frac{40 \pm 2\sqrt{94}}{18} \\[0.8em] &= \frac{20\pm\sqrt{94}}{9} \end{align*}\]
\[\left( x_{1} = \frac{20 - \sqrt{94}}{9} \approx 1{,}14 \right)\]
\[x_{2} = \frac{20 + \sqrt{94}}{20} \approx 3{,}30\]
\(x = \dfrac{20 + \sqrt{94}}{9}\) ist einzige Lösung der Wurzelgleichung.
Beispielaufgaben
1. Beispielaufgabe
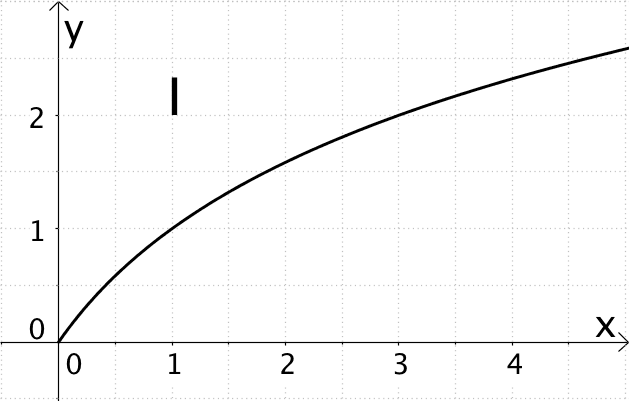
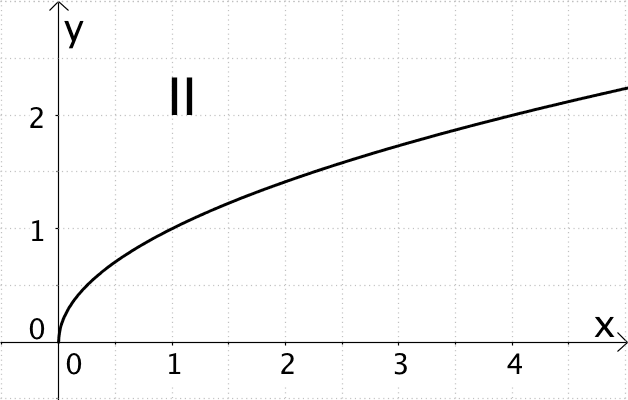
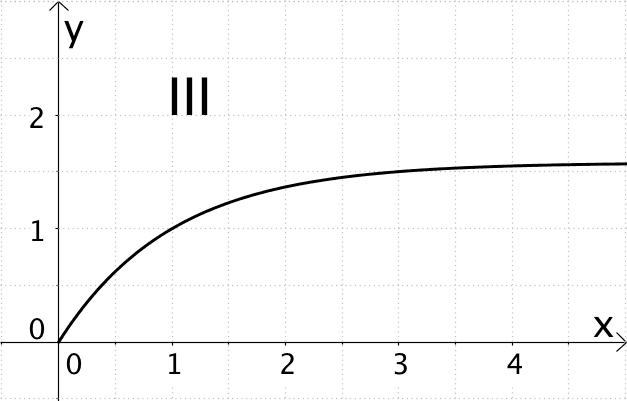
Einer der Graphen I, II oder III zeigt den Graphen der Funktion \(f(x) = \sqrt{x}\). Entscheiden Sie welcher und begründen Sie Ihre Wahl anhand geeigneter Aussagen über den Verlauf der Graphen I, II und III.
Graph II zeigt den Graphen der Funktion \(f\).
Begründung:
Graph III zeigt für \(x \to + \infty\) einen asymptotischen Verlauf. Zudem verläuft Graph III nicht durch den Punkt \((4|2) \; (\sqrt{4} = 2)\). Graph III kommt daher nicht als Graph der Funktion \(f\) in Frage.
Graph I nähert sich dem Koordinatenursprung mit einer Steigung von etwas größer als Eins. Zudem verläuft Graph I nicht durch den Punkt \((4|2)\). Graph I kommt daher nicht als Graph der Funktion \(f\) in Frage.
Graph II nähert sich steil dem Koordinatenursprung und verläuft durch den Punkt \((4|2)\). Graph II zeigt den Graphen der Funktion \(f\).
2. Beispielaufgabe
Der Graph \(G_{f}\) der Funktion \(f \colon x \mapsto \frac{1}{2} \sqrt{8x - 4} + x\) und der Graph \(G_{g}\) der Funktion \(g \colon x \mapsto \frac{1}{2} \sqrt{2x - 1} + 4\) schneiden sich im Punkt \(S\). Berechnen Sie die Schnittstelle \(x_{S}\).
\[f(x) = \frac{1}{2} \sqrt{8x - 4} + x\]
\[g(x) = \frac{1}{2} \sqrt{2x - 1} + 4\]
Für die Berechnung der Schnittstelle \(x_{S}\) werden die Funktionsterme \(f(x)\) und \(g(x)\) gleichgesetzt.
\[\begin{align*} f(x) &= g(x) \\[0.8em] \frac{1}{2} \sqrt{8x - 4} + x &= \frac{1}{2} \sqrt{2x - 1} + 4 \end{align*}\]
Eine Vorbetrachtung der möglichen Lösungen der Wurzelgleich fällt leichter, wenn die Gleichung zunächst vereinfacht wird. In diesem Fall ist es möglich, die beiden Wurzelausdrücke zu einem Wurzelausdruck zusammenzufassen.
\[\begin{align*} \frac{1}{2} \sqrt{8x - 4} + x &= \frac{1}{2} \sqrt{2x - 1} + 4 \\[0.8em] \frac{1}{2}\sqrt{4 \cdot (2x - 1)} + x &= \frac{1}{2}\sqrt{2x - 1} + 4 & &| \; \sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b} \\[0.8em] \frac{1}{2} \cdot 2 \cdot \sqrt{2x - 1} + x &= \frac{1}{2}\sqrt{2x - 1} + 4 \\[0.8em] \sqrt{2x - 1} + x &= \frac{1}{2}\sqrt{2x - 1} + 4 & &| - \frac{1}{2}\sqrt{2x - 1} - x \\[0.8em] \frac{1}{2}\sqrt{2x - 1} &= 4 - x \end{align*}\]
1. Bedingung: Der Radikand der verbleibenden Wurzel darf nicht negativ werden.
2. Bedingung: Eine Quadratwurzel ist stets größer oder gleich Null. Folglich muss auch der Term \(4 - x\) größer oder gleich Null sein.
1. Bedingung
\[\begin{align*} 2x - 1 &\geq 0 & &| + 1 \\[0.8em] 2x &\geq 1 & &| : 2 \\[0.8em] x &\geq \frac{1}{2} \end{align*}\]
2. Bedingung
\[\begin{align*} 4 - x &\geq 0 & &| + x \\[0.8em] 4 \geq x \end{align*}\]
Beide Bedingungen müssen gleichzeitig erfüllt sein, sodass nur Lösungen aus dem Intervall \(\frac{1}{2} \leq x \leq 4\) in Frage kommen. Treten im Verlauf des weiteren Lösungsverfahrens Werte außerhalb dieses Intervalls auf, handelt es sich um „Scheinlösungen", welche aufgrund einer nicht äquivalenten Umformung (Quadrieren) entstehen können.
Wurzelausdruck durch Quadrieren beseitigen:
\[\begin{align*}\frac{1}{2}\sqrt{2x - 1} &= 4 - x & &| \; (\dots)^{2} \; \text{Gleichung quadrieren} \\[0.8em] \frac{1}{4} \cdot (2x - 1) &= \underbrace{(4 - x)^{2}}_{\large{(a\,-\,b)^{2}}} & &| \; \text{2. Binomische Formel} \\[0.8em] \frac{1}{2}x - \frac{1}{4} &= \underbrace{16 - 8x + x^{2}}_{\large{a^{2}\,-\,2ab\,+\,b^{2}}} \end{align*}\]
Quadratische Gleichung formulieren und Lösungsformel für quadratische Gleichungen anwenden (vgl. Abiturskript - 1.1.2 Quadratische Funktion, Lösungsformel für quadratische Gleichungen, vgl. Merkhilfe):
\[\begin{align*} \frac{1}{2}x - \frac{1}{4} &= 16 - 8x + x^{2} & &| - \frac{1}{2}x + \frac{1}{4} \\[0.8em] 0 &= x^{2} - 8{,}5x + 16{,}25 \end{align*}\]
\[\begin{align*}x_{1,2} &= \frac{8{,}5 \pm \sqrt{(-8{,}5)^{2} - 4 \cdot 1 \cdot 16{,}25}}{2 \cdot 1} \\[0.8em] &= \frac{8{,}5 \pm \sqrt{7{,}25}}{2} \end{align*}\]
\[x_{1} = \frac{8{,}5 - \sqrt{7{,}25}}{2} \approx 2{,}90\]
\[\left( x_{2} = \frac{8{,}5 + \sqrt{7{,}25}}{2} \approx 5{,}60 \right)\]
Der Graph der Funktion \(f\) und der Graph der Funktion \(g\) schneiden sich an der Stelle \(x_{S} = 2{,}90\).
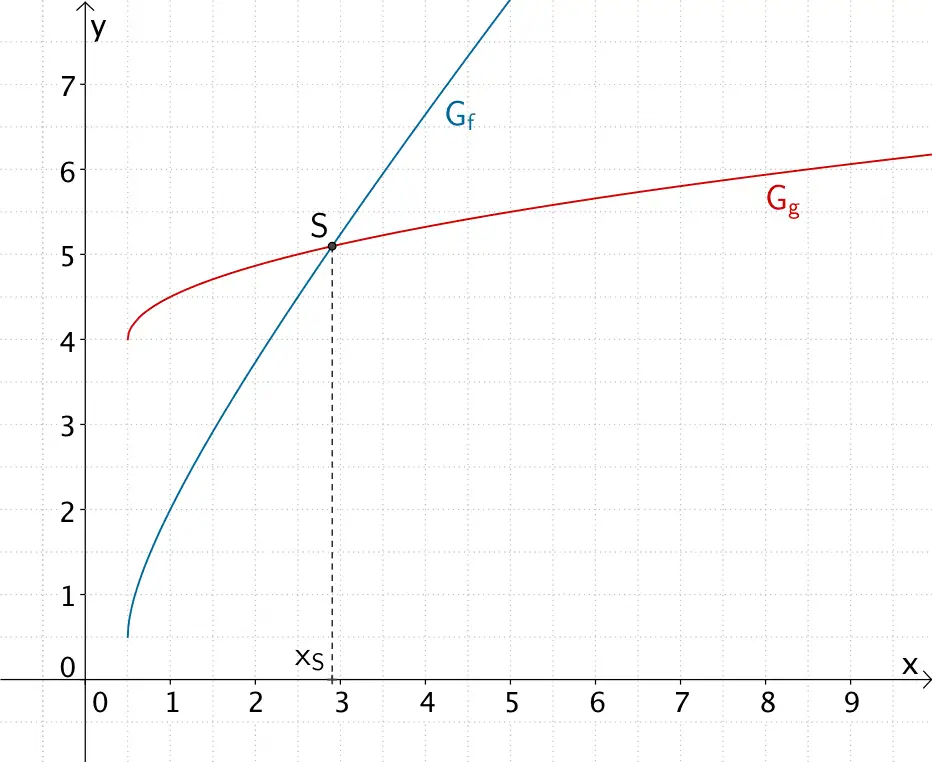
Schnittstelle \(x_{S}\) des Graphen der Funktion \(f \colon x \mapsto \frac{1}{2} \sqrt{8x - 4} + x\) und des Graphen der Funktion \(g \colon x \mapsto \frac{1}{2}\sqrt{2x - 1} + 4\)


