Betrachtet wird die in \([1;+\infty[\) definierte Funktion \(h\) mit \(h(x) = f(x)\).
Begründen Sie, dass die Funktion \(f\) nicht umkehrbar, die Funktion \(h\) jedoch umkehrbar ist. Geben Sie den Definitions- und Wertebereich der Umkehrfunktion von \(h\) an.
(6 BE)
Lösung zu Teilaufgabe 1c
\[f(x) = 5x \cdot e^{-x}; \; D_f = \mathbb R\]
\[h(x) = f(x); \; D_h = [1;+\infty[\]
Begründungen, weshalb \(f\) nicht umkehrbar und \(h\) umkehrbar ist
Die Begründungen können zweckmäßig mithilfe von Abbildung 1 oder unter Berücksichtigung des einzigen Extrempunkts \(\big(1|\frac{5}{e}\big)\) des Graphen von \(f\) erfolgen (vgl. Teilaufgabe 1a).
Kriterium für die Umkehrbarkeit einer Funktion
Ist eine Funktion \(f\) auf ihrem Definitionsbereich bzw. einem Teilbereich des Definitionsbereichs entweder nur streng monoton zunehmend oder nur streng monoton abnehmend, ist sie dort umkehrbar.
Graphische Untersuchung der Umkehrbarkeit: Wenn jede Parallele zur \(x\)-Achse den Funktionsgraphen höchstens einmal schneidet, ist die Funktion im dargestellten Bereich umkehrbar.
Graph einer im dargestellten Bereich umkehrbaren Funktion
Graph einer im dargestellten Bereich nicht umkehrbaren Funktion
Mögliche Begründungen, weshalb \(f\) nicht umkehrbar ist:
ergänzende Darstellung
Aus Abbildung 1 ist ersichtlich, dass es Parallelen zur \(x\)-Achse gibt, die den Graphen \(G\) zweimal schneiden. Deshalb ist \(f\) in \(\mathbb R\) nicht umkehrbar.
ergänzende Darstellung
Abbildung 1 ist zu entnehmen, dass es beispielsweise zwei \(x\)-Werte mit dem Funktionswert \(f(x) = 1\) gibt. Deshalb ist \(f\) in \(\mathbb R\) nicht umkehrbar.
weitere mögliche Begründung:
Die Funktion \(f\) ist in \(\mathbb R\) nicht umkehrbar, da sie an der Extremstelle \(x = 1\) das Monotonieverhalten wechselt.
Mögliche Begründungen, weshalb \(h\) umkehrbar ist:
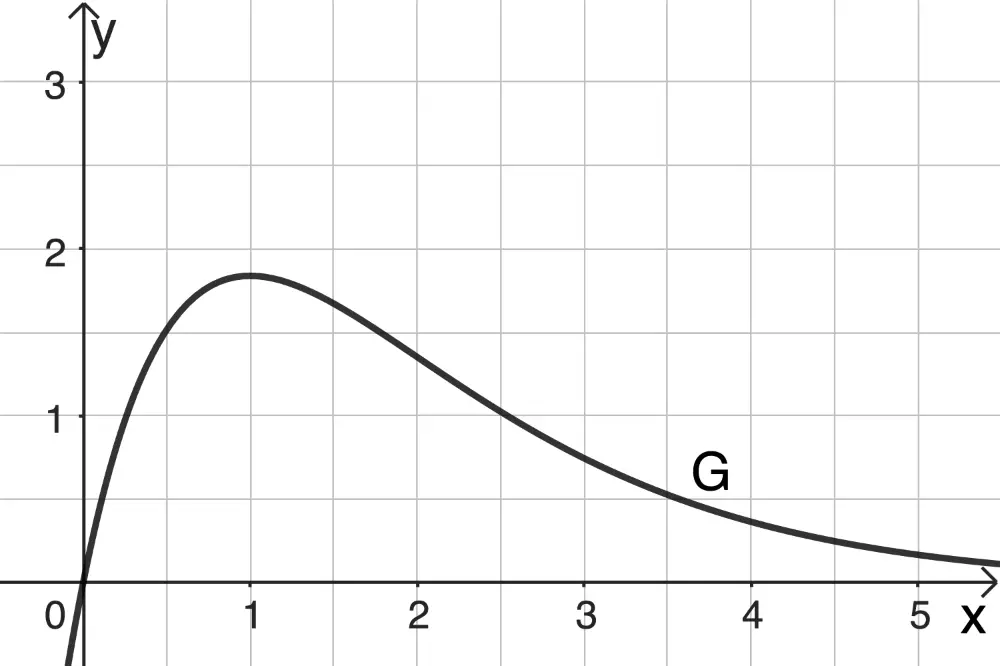Abb. 1
Graph der in \(\mathbb R\) definierten Funktion \(f\)
ergänzende Darstellung
Graph der Funktion \(h\) mit \(D_h = [1;+\infty[\)
Da die Funktion \(f\) nur die Extremstelle \(x = 1\) besitzt und Abbildung 1 dort einen Hochpunkt zeigt, ist die Funktion \(h\) auf ihrem Definitionsbereich \([1;+\infty[\) streng monoton abnehmend und deshalb umkehrbar.
rechnerische Begründung:
\(h'(x) = f'(x) = \textcolor{#0087c1}{\underbrace{(-5x+5)}_{\substack{\large{\leq \,0 \; \text{für}} \\ \large{x\, \in\, [1;+\infty[}}}} \cdot \textcolor{#e9b509}{\underset{>\,0}{e^{-x}}} \textcolor{#cc071e}{\leq 0}\) (vgl. Teilaufgabe 1a)
Mit \(h'(x) \textcolor{#cc071e}{\leq 0}\) für \(x \in [1;+\infty[\) ist die Funktion \(h\) auf ihrem Definitionsbereich streng monoton abnehmend und deshalb umkehrbar.
Definitions- und Wertebereich der Umkehrfunktion von \(h\)
Definitionsbereich der Umkehrfunktion von \(h\): \(\big]0;\frac{5}{e}\big]\)
Wertebereich der Umkehrfunktion von \(h\): \([1;+\infty[\)
Ergänzende Erklärung (nicht verlangt)
Der Definitionsbereich der Umkehrfunktion von \(h\) entspricht dem Wertebereich von \(h\) und der Wertebereich der Umkehrfunktion von \(h\) entspricht dem Definitionsbereich von \(h\).
Funktionsterm einer Umkehrfunktion bestimmen
1. Funktionsgleichung \(y = f(x)\) nach \(x\) auflösen.
2. Variablen \(x\) und \(y\) tauschen.
3. Funktionsterm \(y = f^{-1}(x)\) mit Definitions- und Wertemenge angeben. Es gilt: \(D_{f^{-1}} = W_f\) und \(W_{f^{-1}} = D_f\).
Es ist ebenso möglich, zuerst die Variablen zu tauschen, und anschließend die Gleichung \(x = f(y)\) nach \(y\) aufzulösen.
Funktionsgraph einer Umkehrfunktion skizzieren
Der Graph \(\textcolor{#cc071e}{G_{f^{-1}}}\) der Umkehrfunktion entsteht durch Spiegelung des Graphen \(G_f\) an der Winkelhalbierenden des I. und III. Quadranten mit der Gleichung \(\textcolor{#e9b509}{y = x}\). Existieren Schnittpunkte von \(G_f\) mit der Winkelhalbierenden, sind diese Fixpunkte der Spiegelung und somit Schnittpunkte von \(G_f\) und \(\textcolor{#cc071e}{G_{f^{-1}}}\).
Der Definitionsbereich von \(h\) ist mit \([1;+\infty[\) gegeben.
Wertebereich von \(h\):
Der Wertebereich von \(h\) ergibt sich mithilfe von Abbildung 1 und/oder nachfolgender Überlegung.
Da die Funktion \(h\) auf ihrem Definitionsbereich \([1;+\infty[\) streng monoton abnehmend ist, beschränkt einerseits das globale Maximum \(h(1) = f(1) = \frac{5}{e}\) und andererseits das Verhalten für \(x \to +\infty\) den Wertebereich von \(h\).
\[\lim \limits_{x\,\to\,+\infty} h(x) = \lim \limits_{x\,\to\,+\infty} 5x \cdot e^{-x} = \lim \limits_{x\,\to\,+\infty} \frac{5x}{e^x} = 0\]
Abb. 1
Wichtige Grenzwerte (jeweils \(r > 0\))
\(\lim \limits_{x \,\to\,+\infty} \dfrac{x^r}{e^x} = 0\)
Für \(x \to +\infty\) wächst \(e^x\) schneller als \(x^r\).
\(\lim \limits_{x\,\to\,+\infty} \dfrac{\ln{x}}{x^r} = 0\)
Für \(x \to +\infty\) wächst \(x^r\) schneller als \(\ln{x}\).
\[\lim \limits_{x\,\to\,0} \left(x^r \cdot \ln{x}\right) = 0\]
Somit ist \(\big]0;\frac{5}{e}\big]\) der Wertebereich von \(h\).
