Die Gerade \(g\) verläuft durch die Punkte \(A\,(0|1|2)\) und \(B\,(2|5|6)\).
Zeigen Sie, dass die Punkte \(A\) und \(B\) den Abstand 6 haben.
Die Punkte \(C\) und \(D\) liegen auf \(g\) und haben von \(A\) jeweils den Abstand 12. Bestimmen Sie die Koordinaten von \(C\) und \(D\).
(3 BE)
Lösung zu Teilaufgabe 1a
Abstand zweier Punkte, Koordinaten eines Punktes auf einer Geraden
\[A\,(0|1|2)\,, \enspace B\,(2|5|6)\]
\[A, B \in g\]
\[C, D \in g\,, \enspace d\,(A;C) = d\,(A;D) = 12\]
Nachweis, dass die Punkte \(A\) und \(B\) den Abstand 6 haben
Betrag eines Vektors
\[ \vert \overrightarrow{a} \vert = \sqrt{\overrightarrow{a} \circ \overrightarrow{a}} = \sqrt{{a_1}^2 + {a_2}^2 + {a_3}^2}\]
(vgl. Merkhilfe)
\[\begin{align*} d\,(A;B) = \overline{AB} &= \vert \overrightarrow{AB} \vert \\[0.8em] &= \vert \overrightarrow{B} - \overrightarrow{A} \vert \\[0.8em] &= \left| \begin{pmatrix} 2 \\ 5 \\ 6 \end{pmatrix} - \begin{pmatrix} 0 \\ 1 \\ 2 \end{pmatrix} \right| \\[0.8em] &= \left| \begin{pmatrix} 2 \\ 4 \\ 4 \end{pmatrix} \right| \\[0.8em] &= \sqrt{2^{2} + 4^{2} + 4^{2}} \\[0.8em] &= \sqrt{36} \\[0.8em] &= 6 \end{align*}\]
Koordinaten der Punkte \(C\) und \(D\)
\[A\,(0|1|2)\,, \enspace B\,(2|5|6)\]
\[A, B \in g\]
\[C, D \in g\,, \enspace d\,(A;C) = d\,(A;D) = 12\]
1. Lösungsansatz: Vektoraddition
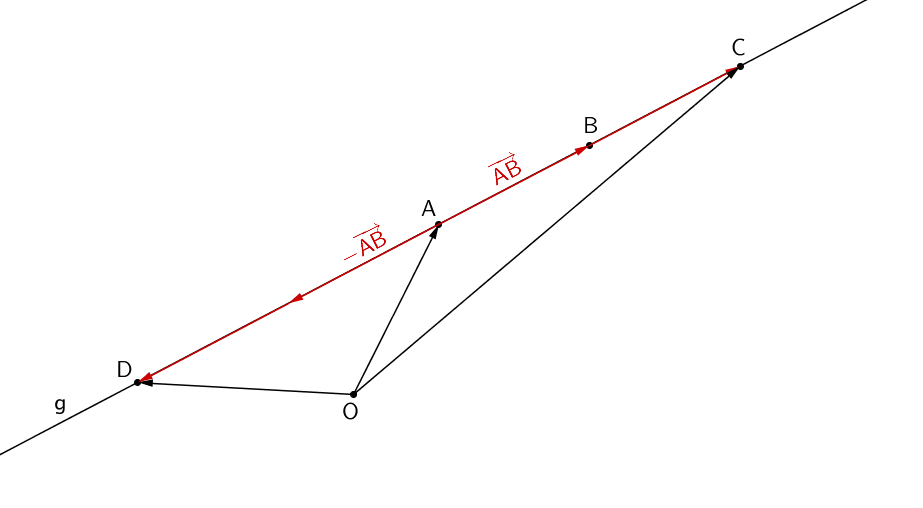
Mit \(\overline{AB} = 6\) (siehe oben) können die Ortsvektoren \(\overrightarrow{C}\) und \(\overrightarrow{D}\) durch Vektoraddition des Ortsvektors \(\overrightarrow{A}\) und dem Doppelten des Vektors \(\overrightarrow{AB}\) bzw. dessen Gegenvektor \(-\overrightarrow{AB}\) berechnet werden (Zeichnung nicht maßstabsgetreu).
Koordinaten des Punktes \(C\):
\(\overrightarrow{AB} = \begin{pmatrix} 2 \\ 4 \\ 4 \end{pmatrix}\) (siehe oben)
\[\begin{align*} \overrightarrow{C} &= \overrightarrow{A} + 2 \cdot \overrightarrow{AB} \\[0.8em] &= \begin{pmatrix} 0 \\ 1 \\ 2 \end{pmatrix} + 2 \cdot \begin{pmatrix} 2 \\ 4 \\ 4 \end{pmatrix} \\[0.8em] &= \begin{pmatrix} 0 \\ 1 \\ 2 \end{pmatrix} + \begin{pmatrix} 4 \\ 8 \\ 8 \end{pmatrix} \\[0.8em] &= \begin{pmatrix} 4 \\ 9 \\ 10 \end{pmatrix} \end{align*}\]
\[\Longrightarrow \quad C\,(4|9|10)\]
Probe:
Betrag eines Vektors
\[ \vert \overrightarrow{a} \vert = \sqrt{\overrightarrow{a} \circ \overrightarrow{a}} = \sqrt{{a_1}^2 + {a_2}^2 + {a_3}^2}\]
(vgl. Merkhilfe)
\[\begin{align*} d\,(A;C) = \overline{AC} &= \vert \overrightarrow{AC} \vert \\[0.8em] &= \vert \overrightarrow{C} - \overrightarrow{A} \vert \\[0.8em] &= \left| \begin{pmatrix} 4 \\ 9 \\ 10 \end{pmatrix} - \begin{pmatrix} 0 \\ 1 \\ 2 \end{pmatrix} \right| \\[0.8em] &= \left| \begin{pmatrix} 4 \\ 8 \\ 8 \end{pmatrix} \right| \\[0.8em] &= \sqrt{4^{2} + 8^{2} + 8^{2}} \\[0.8em] &= \sqrt{144} \\[0.8em] &= 12 \end{align*}\]
Koordinaten des Punktes \(D\):
\(\overrightarrow{AB} = \begin{pmatrix} 2 \\ 4 \\ 4 \end{pmatrix}\) (siehe oben)
\[\begin{align*} \overrightarrow{D} &= \overrightarrow{A} + 2 \cdot (-\overrightarrow{AB}) \\[0.8em] &= \begin{pmatrix} 0 \\ 1 \\ 2 \end{pmatrix} + 2 \cdot \begin{pmatrix} -2 \\ -4 \\ -4 \end{pmatrix} \\[0.8em] &= \begin{pmatrix} 0 \\ 1 \\ 2 \end{pmatrix} - \begin{pmatrix} 4 \\ 8 \\ 8 \end{pmatrix} \\[0.8em] &= \begin{pmatrix} -4 \\ -7 \\ -6 \end{pmatrix} \end{align*}\]
\[\Longrightarrow \quad D\,(-4|-7|-6)\]
Probe:
Betrag eines Vektors
\[ \vert \overrightarrow{a} \vert = \sqrt{\overrightarrow{a} \circ \overrightarrow{a}} = \sqrt{{a_1}^2 + {a_2}^2 + {a_3}^2}\]
(vgl. Merkhilfe)
\[\begin{align*} d\,(A;D) = \overline{AD} &= \vert \overrightarrow{AD} \vert \\[0.8em] &= \vert \overrightarrow{D} - \overrightarrow{A} \vert \\[0.8em] &= \left| \begin{pmatrix} -4 \\ -7 \\ -6 \end{pmatrix} - \begin{pmatrix} 0 \\ 1 \\ 2 \end{pmatrix} \right| \\[0.8em] &= \left| \begin{pmatrix} -4 \\ -8 \\ -8 \end{pmatrix} \right| \\[0.8em] &= \sqrt{(-4)^{2} + (-8)^{2} + (-8)^{2}} \\[0.8em] &= \sqrt{144} \\[0.8em] &= 12 \end{align*}\]
2. Lösungsansatz: Länge einer Strecke / Abstand zweier Punkte auf einer Geraden
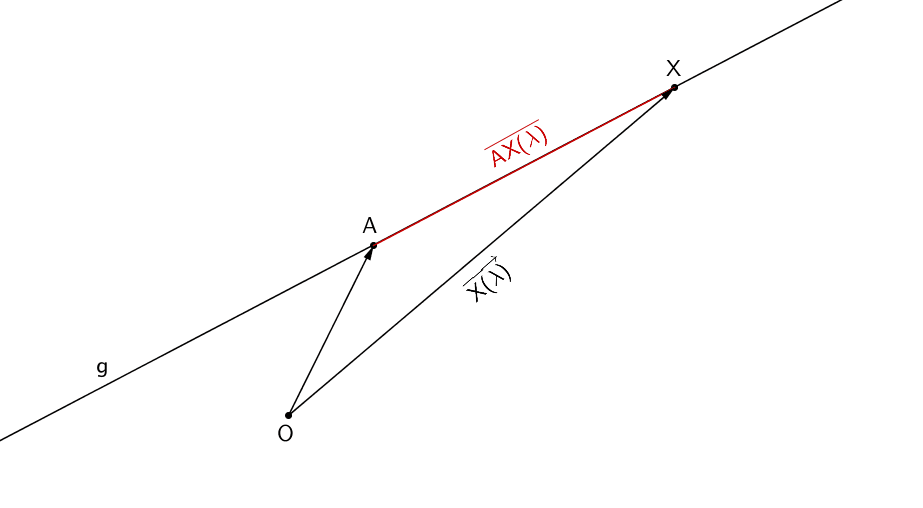
Unabhängig von dem Teilergebnis \(\overline{AB} = 6\) (siehe oben), lässt sich der Abstand \(d\,(X;A)\) eines beliebigen Punktes \(X \in g\) in Abhängigkeit des Parameters \(\lambda\) der Geradengleichung von \(g\) formulieren. Die Bedingung \(\overline{AX(\lambda)} = 12\) liefert die Parameterwerte für \(\lambda\), um die Koordinaten der Punkte \(C\) und \(D\) berechnen zu können (Zeichnung nicht maßstabsgetreu).
Gleichung der Gerden \(g\):
Es sei \(A\) der Aufpunkt der Geraden \(g\) und \(\overrightarrow{AB}\) der Richtungsvektor von \(g\).
\(A\,(0|1|2)\,, \enspace \overrightarrow{AB} = \begin{pmatrix} 2 \\ 4 \\ 4 \end{pmatrix}\) (siehe oben)
\[\begin{align*} g \colon \overrightarrow{X} &= \overrightarrow{A} + \lambda \cdot \overrightarrow{AB} \\[0.8em] g \colon \overrightarrow{X} &= \begin{pmatrix} 0 \\ 1 \\ 2 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 2 \\ 4 \\ 4 \end{pmatrix} \end{align*}\]
Bedingung \(d\,(X;A) = \overline{AX(\lambda)} = 12\) formulieren:
Betrag eines Vektors
\[ \vert \overrightarrow{a} \vert = \sqrt{\overrightarrow{a} \circ \overrightarrow{a}} = \sqrt{{a_1}^2 + {a_2}^2 + {a_3}^2}\]
(vgl. Merkhilfe)
\[\begin{align*} d\,(X;A) &= 12 \\[0.8em] \overline{AX(\lambda)} &= 12 \\[0.8em] \vert \overrightarrow{AX(\lambda)} \vert &= 12 \\[0.8em] \vert \overrightarrow{X(\lambda)} - \overrightarrow{A} \vert &= 12 & &| \; X \in g \\[0.8em] \left| \begin{pmatrix} 2\lambda \\ 1 + 4\lambda \\ 2 + 4\lambda \end{pmatrix} - \begin{pmatrix} 0 \\ 1 \\ 2 \end{pmatrix} \right| &= 12 \\[0.8em] \left| \begin{pmatrix} 2\lambda \\ 4\lambda \\ 4\lambda \end{pmatrix} \right| &= 12 \\[0.8em] \sqrt{(2\lambda)^{2} + (4\lambda)^{2} + (4\lambda)^{2}} &= 12 \\[0.8em] \sqrt{4{\lambda}^{2} + 16{\lambda}^{2} + 16{\lambda}^{2}} &= 12 \\[0.8em] \sqrt{36{\lambda}^{2}} &= 12 \\[0.8em] \pm 6\lambda &= 12 & &| : 6 \\[0.8em] \pm \lambda &= 2 \end{align*}\]
\[\lambda_{1} = 2\,; \enspace \lambda_{2} = -2\]
Zur Berechnung der Koordinaten der Punkte \(C\) und \(D\) werden die Parameterwerte \(\lambda_{1}\) und \(\lambda_{2}\) jeweils in die Geradengleichung der Geraden \(g\) eingesetzt.
\[g \colon \overrightarrow{X} = \begin{pmatrix} 0 \\ 1 \\ 2 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 2 \\ 4 \\ 4 \end{pmatrix}\]
\[\overrightarrow{C} = \begin{pmatrix} 0 \\ 1 \\ 2 \end{pmatrix} + 2 \cdot \begin{pmatrix} 2 \\ 4 \\ 4 \end{pmatrix} = \begin{pmatrix} 4 \\ 9 \\ 10 \end{pmatrix}\]
\[\overrightarrow{D} = \begin{pmatrix} 0 \\ 1 \\ 2 \end{pmatrix} - 2 \cdot \begin{pmatrix} 2 \\ 4 \\ 4 \end{pmatrix} = \begin{pmatrix} -4 \\ -7 \\ -6 \end{pmatrix}\]
Anmerkung: Unter Berücksichtigung des Teilergebnisses \(\overline{AB} = 6\) (siehe oben) beschreibt der erste Lösungsansatz mithilfe der Vektoraddition den schnellere Lösungsweg, um die Koordinaten der Punkte \(C\) und \(D\) zu berechnen. Der zweite Lösungsansatz kann generell gewählt werden, wenn die Koordinaten eines Punktes auf einer Geraden mit einem festen Abstand zu einem anderen gegebenen Punkt auf der Geraden berechnet werden sollen.


