Bei der Jubiläumsfeier können CDs sowohl zu einem Preis von 9 Euro pro Stück gekauft als auch bei einem Spiel gewonnen werden. Für das Spiel wird ein Glücksrad mit einem grauen und einem weißen Sektor verwendet (vgl. Abbildung). Für einen Einsatz von einem Euro wird das Glücksrad dreimal gedreht. Nur wenn dabei genau zweimal der grau markierte Sektor getroffen wird, erhält man eine CD. Die Größe des Öffnungswinkels des grauen Sektors im Bogenmaß wird mit \(b\) bezeichnet.
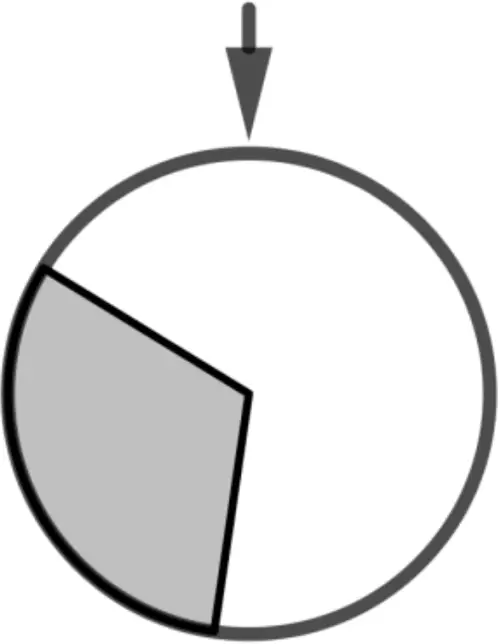
Zeigen Sie, dass die Wahrscheinlichkeit dafür, bei diesem Spiel eine CD zu erhalten, mithilfe des Terms \(\dfrac{3}{4\pi^2}b^2 - \dfrac{3}{8\pi^3}b^3\) berechnet werden kann.
(4 BE)
Lösung zu Teilaufgabe 3a
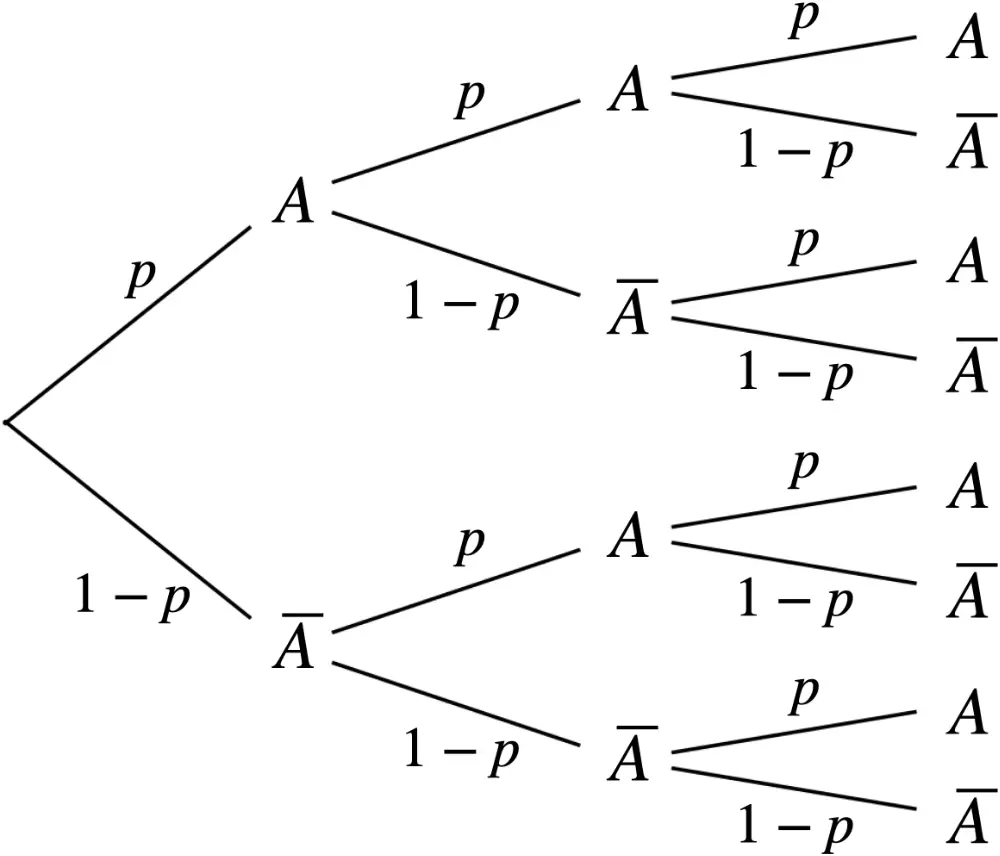
Es liegt eine Bernoulli-Kette der Länge \(n = 3\) vor. Die Wahrscheinlichkeit dafür, dass der graue Sektor getroffen wird, ist mit \(p\) konstant (Trefferwahrscheinlichkeit).
Bernoulli-Experiment, Bernoulli-Kette
Ein Zufallsexperiment, bei dem nur zwei sich gegenseitig ausschließende Ereignisse \(A\) und \(\overline{A}\) eintreten können, heißt Bernoulli-Experiment.
Ein betrachtetes Ereignis \(A\) wird als Treffer mit der Trefferwahrscheinlichkeit \(p\) und dessen Gegenereignis \(\overline{A}\) als Niete mit der Wahrscheinlichkeit \(q = 1- p\) bezeichnet.
Wird ein Bernoulli-Experiment \(n\)-mal hintereinander ausgeführt, und ist dabei die Trefferwahrscheinlichkeit \(p\) bei jeder Durchführung des Experiments konstant, entsteht eine Bernoulli-Kette der Länge \(n\) mit dem Parameter \(p\).
Zufallsgröße \(X\) (wird eingeführt): Gibt die Anzahl an, wie oft der graue Sektor getroffen wird.
Die Zufallsgröße \(X\) ist binomialverteilt nach \(B(3;p)\).
Binomialverteilte Zufallsgröße
Eine Zufallsgröße \(X\), die bei einer Bernoulli-Kette der Länge \(n\) die Anzahl der Treffer \(k \in \{0;1;\dots;n\}\) mit der Trefferwahrscheinlichkeit \(p\) angibt, heißt binomialverteilt nach \(B(n;p)\).
Binomialverteilung
Die Wahrscheinlichkeitsverteilung einer \(B(n;p)\)-verteilten Zufallsgröße \(X\) heißt Binomialverteilung.
Es gilt: \(\displaystyle P_{p}^{n}(X = k) = B(n;p;k) = \binom{n}{k} \cdot p^{k} \cdot (1 - p)^{n - k}\) mit \(k = \{0;1;\dots;n\}\) (Bernoulli-Formel)*
Kumulative Verteilungsfunktion einer \(\boldsymbol{B(n;p)}\)-verteilten Zufallsgröße \(\boldsymbol{X}\)
\(F_p^n(k) = P_p^n(X \leq k) = \sum \limits_{i\,=\,0}^k B(n;p;i)\) (von \(X = 0\) bis \(X = k\) aufsummierte Einzelwahrscheinlichkeiten \(B(n;p;i)\))*
* Kann mit dem wissenschaftlichen Taschenrechner (WTR) oder ggf. mit dem Tafelwerk (TW) bestimmt werden.
\[\begin{align*}P(\text{Gewinn (CD)}) = P_p^3(X = 2) &= \binom{3}{2} \cdot p^2 \cdot (1-p)^{3\,-\,2} \\[0.8em] &= 3 \cdot p^2 \cdot (1 - p) \\[0.8em] &= 3 \cdot (p^2 - p^3)\end{align*}\]
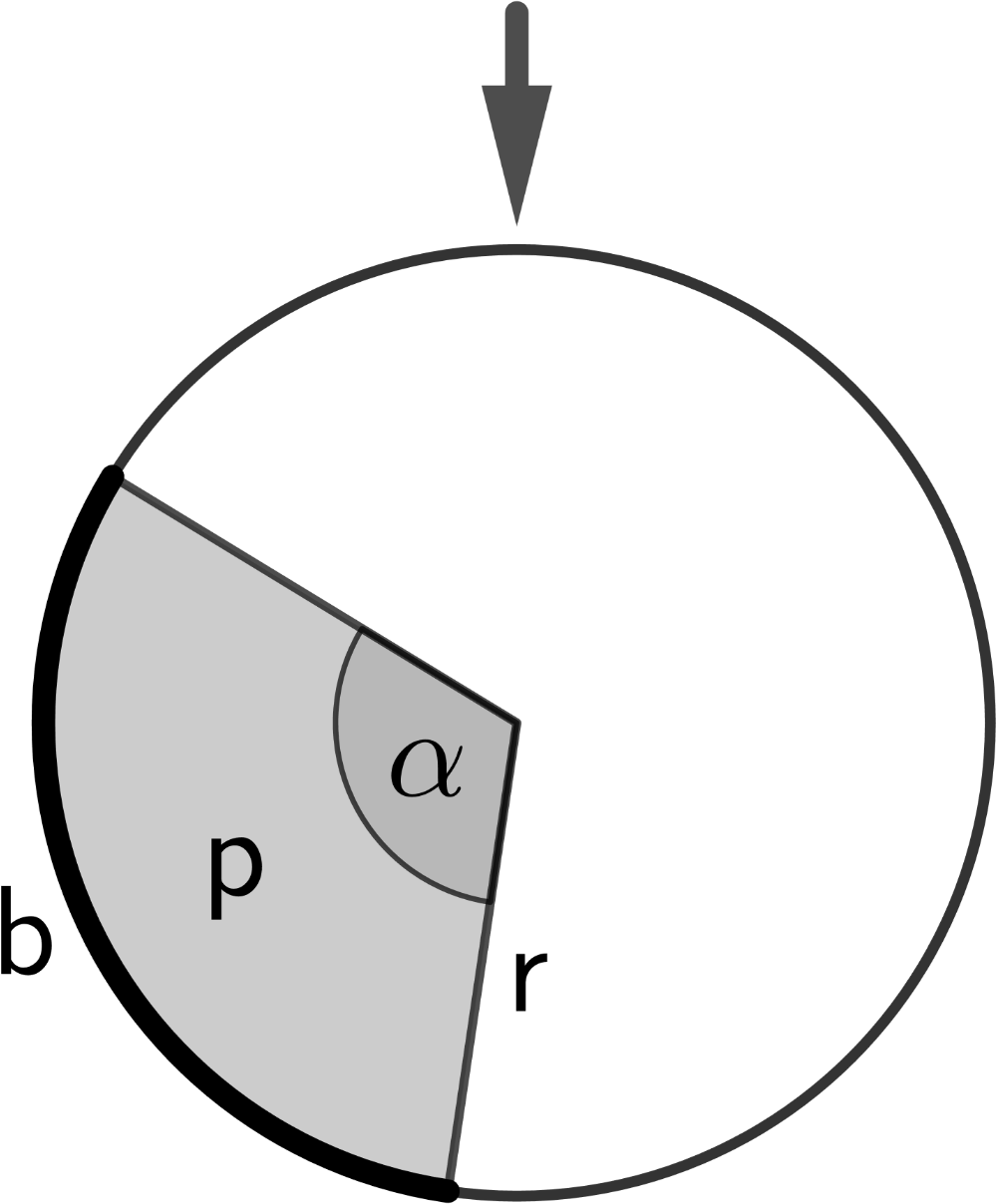
Glücksrad mit grauem Sektor und dessen zugehörigem Mittelpunktswinkel \(\alpha\) bzw. zugehöriger Bogenlänge \(b\)
Anteil \(p\) der Fläche des grauen Sektors an der Kreisfläche:
\[p = \frac{A_{\text{Sektor}}}{A_{\text{Kreis}}} = \frac{\frac{b}{2\pi}\cdot \cancel{r^2\pi}}{\cancel{r^2\pi}} = \frac{b}{2\pi}\]
oder
\[p = \frac{\alpha}{360^{\circ}} = \frac{b}{2\pi}\]
Damit ergibt sich:
\[\begin{align*}P(\text{Gewinn (CD)}) &= 3 \cdot (p^2 - p^3) \\[0.8em] &= 3 \cdot \left( \left( \frac{b}{2\pi} \right)^2 - \left( \frac{b}{2\pi} \right)^3 \right) \\[0.8em] &= 3 \cdot \left( \frac{b^2}{4\pi^2} - \frac{b^3}{8\pi^3} \right) \\[0.8em] &= \frac{3}{4\pi^2}b^2 - \frac{3}{8\pi^3}b^3 \end{align*}\]


