Die nebenstehende Abbildung 2 zeigt den Graphen einer Funktion \(f\).

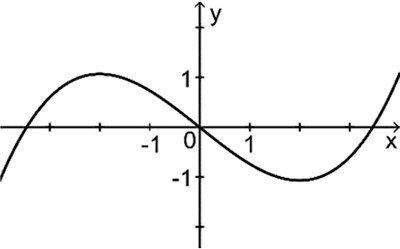Abb. 2

Einer der folgenden Graphen I, II und III gehört zur ersten Ableitungsfunktion von \(f\). Geben Sie diesen an. Begründen Sie, dass die beiden anderen Graphen dafür nicht infrage kommen.

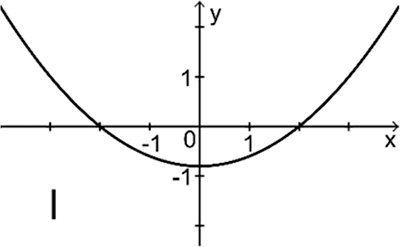
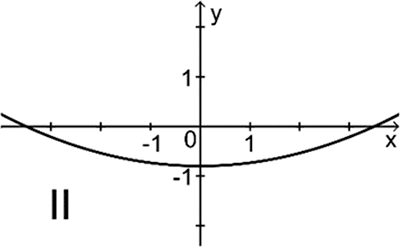
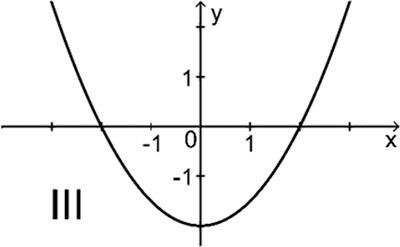Abb. 3

(3 BE)

Lösung zu Teilaufgabe 3a

Mögliche Vorgehensweise:

Der Graph von \(f\) zeigt unter anderem folgende Eigenschaften: zwei Extrempunkte und einen Wendepunkt.

Es gilt:

Die Extremstellen des Graphen einer Funktion sind die Nullstellen des Graphen der zugehörigen Ableitungsfunktion.

Im Wendepunkt des Graphen einer Funktion ist die Steigung des Graphen extremal (Steigung der Wendetangente). Der Graph der zugehörigen Ableitungsfunktion besitzt an der Wendestelle einen Extrempunkt, dessen \(y\)-Koordinate gleich dem Wert der Steigung der Wendetangente ist. 

Graph I gehört zur Ableitungsfunktion von \(f\).

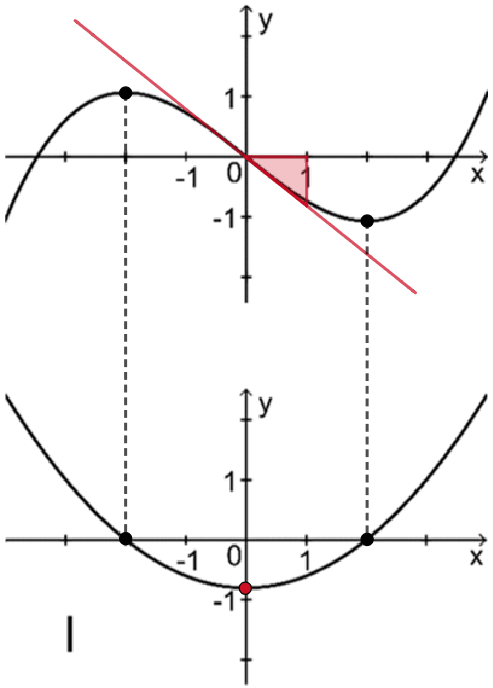
Begründung, dass die beiden anderen Graphen nicht infrage kommen

Graph II kommt nicht infrage, da der Graph von \(f\) bei \(x = -2\) und \(x = 2\) jeweils einen Extrempunkt besitzt, Graph II jedoch nicht die Nullstellen \(x = -2\) und \(x = 2\) zeigt.

Graph III kommt nicht infrage, da der Graph von \(f\) im Wendepunkt \((0|0)\) eine Wendetangente besitzt, deren Steigung größer \(\textcolor{#cc071e}{\mathbf{-1}}\) ist, die \(y\)-Koordinate des Tiefpunkts von Graph III jedoch kleiner \(\mathbf{-1}\) ist.