Das Fenster ist drehbar um eine Achse, die im Modell durch die Mittelpunkte der Strecken \([GH]\) und \([LK]\) verläuft. Die Unterkante des Fensters schwenkt dabei in das Zimmer; das Drehgelenk erlaubt eine zum Boden senkrechte Stellung der Fensterfläche.
Bestimmen Sie die Koordinaten des Mittelpunkts \(M\) der Strecke \([GH]\) und bestätigen Sie rechnerisch, dass das Fenster bei seiner Drehung den Boden nicht berühren kann.
(Teilergebnis: \(M\,(2|5|1{,}5)\))
(4 BE)
Lösung zu Teilaufgabe e
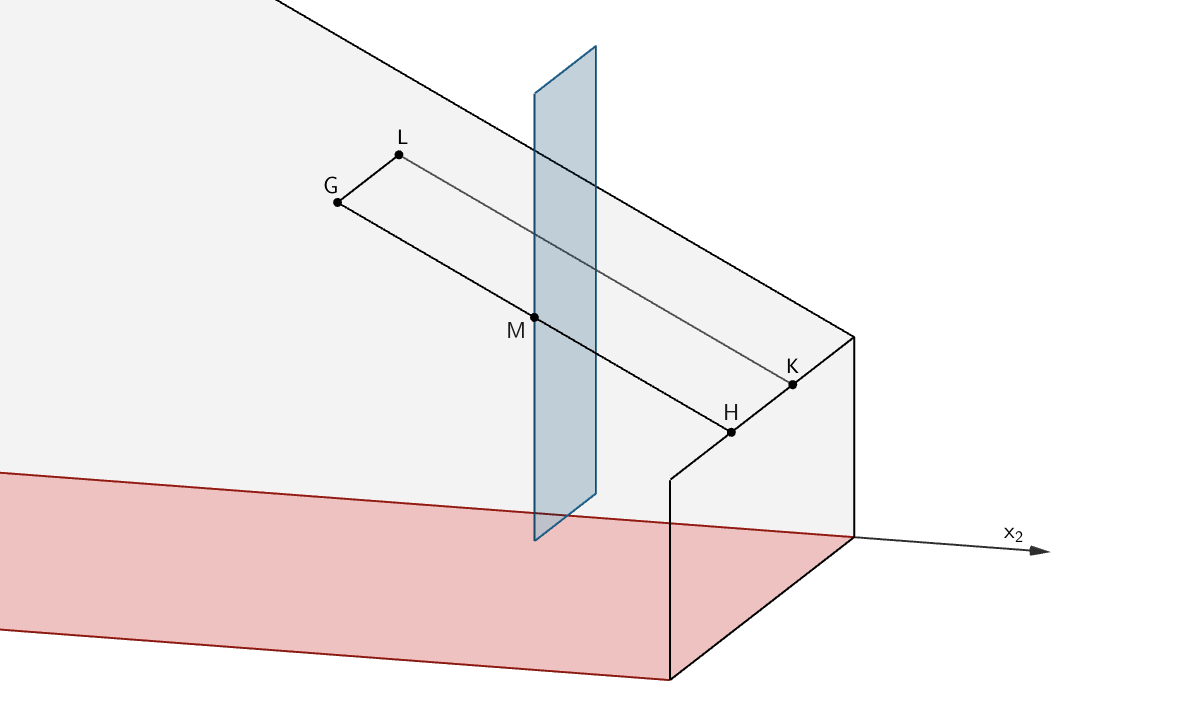
Zum Boden senkrechte Stellung der Fensterfläche
Mittelpunkt der Strecke \([GH]\)
Mittelpunkt einer Strecke
Für den Ortsvektor \(\overrightarrow{M}\) des Mittelpunkts \(M\) einer Strecke \([AB]\) gilt:
\[\overrightarrow{M} = \frac{1}{2} \left( \overrightarrow{A} + \overrightarrow{B} \right)\]
\(G\,(2|4|2)\,, \enspace H\,(2|6|1)\;\) (siehe Teilaifgabe c)
\[M = \frac{1}{2} \cdot \big( \overrightarrow{G} + \overrightarrow{H}\big) = \frac{1}{2} \cdot \left[ \begin{pmatrix} 2 \\ 4 \\ 2 \end{pmatrix} + \begin{pmatrix} 2 \\ 6 \\ 1 \end{pmatrix} \right] = \begin{pmatrix} 2 \\ 5 \\ 1{,}5 \end{pmatrix} \quad \Longrightarrow \quad M\,(2|5|1{,}5)\]
Nachweis, dass das Fenster den Boden nicht berührt
Damit das Fenster bei seiner Drehung den Boden nicht berührt, muss die Länge der Strecke \([MH]\) kleiner sein als der Abstand des Punktes \(M\) von der \(x_1x_2\)-Ebene.
Der Wert der \(x_{3}\)-Koordinate des Punktes \(M\) entspricht dem Abstand des Punktes \(M\) von der \(x_1x_2\)-Ebene.
\[M\,(2|5|\boldsymbol{1{,}5}) \quad \Longrightarrow \quad d\,(M;x_1x_2\text{-Ebene}) = 1{,}5\]
Länge der Strecke \([MH]\) berechnen:
\[\overline{MH} = \frac{1}{2} \cdot \overline{GH} = \frac{1}{2} \cdot \sqrt{5} \approx 1{,}12\]
\[\Longrightarrow \quad \overline{MH} < d\,(M;x_1x_2\text{-Ebene})\]
\(\Longrightarrow \quad\) Das Fenster berührt bei seiner Drehung nicht den Boden.


