Gegeben sind grüne und rote Würfel, deren Seitenflächen unterschiedlich beschriftet sind und beim Werfen mit jeweils gleicher Wahrscheinlichkeit auftreten. Jeder grüne Würfel trägt auf fünf Seitenflächen die Augenzahl 1 und auf einer die Augenzahl 6. Jeder rote Würfel trägt auf jeweils zwei Seitenflächen die Augenzahlen 1, 3 bzw. 6.
In einer Urne befinden sich drei grüne Würfel und zwei rote Würfel. Der Urne werden mit einem Griff zwei Würfel zufällig entnommen. Geben Sie einen Term an, mit dem man die Wahrscheinlichkeit dafür bestimmen kann, dass ein roter Würfel und ein grüner Würfel entnommen werden.
(2 BE)
Lösung zu Teilaufgabe a
Beispielsweise
\[\frac{\displaystyle \binom{2}{1} \cdot \binom{3}{1}}{\displaystyle \binom{5}{2}}\]
oder
\[\frac{2}{5} \cdot \frac{3}{4} + \frac{3}{5} \cdot \frac{1}{2}\]
Begründung (nicht verlangt)
Urne: 3 grüne und 2 rote Würfel
Das vorliegende Zufallsexperiment „Der Urne werden mit einem Griff zwei Würfel zufällig entnommen" lässt sich als zweistufiges Zufallsexperiment nach dem Urnenmodell „Ziehen ohne Zurücklegen und ohne Beachtung der Reihenfolge" auffassen, bei dem die beiden Würfel nacheinander entnommen werden.
1. Möglichkeit: Formel der Merkhilfe verwenden
Urnenmodell: „Ziehen ohne Zurücklegen und ohne Beachtung der Reihenfolge"
Werden aus einer Urne mit \(N\) Kugeln, von denen \(K\) Kugeln schwarz sind, \(n\) Kugeln mit einem Griff, d.h. ohne Zurücklegen und ohne Beachtung der Reihenfolge gezogen, so gilt für die Wahrscheinlichkeit, genau \(k\) schwarze Kugeln zu ziehen:
\[P(\text{„genau}\,k\,\text{schwarze Kugeln"}) = \frac{\displaystyle \binom{K}{k} \cdot \binom{N - K}{n - k}}{\displaystyle \binom{N}{n}}\]
\[P(\text{„genau}\,k\,\text{schwarze Kugeln"}) = \frac{\displaystyle \binom{K}{k} \cdot \binom{N - K}{n - k}}{\displaystyle \binom{N}{n}}\]
In diesem Fall bedeutet beispielsweise
\(N\): 5 Würfel sind in der Urne,
\(n\): 2 Würfel werden mit einem Griff entnommen,
\(\textcolor{#cc071e}{K}\): 2 rote Würfel sind in der Urne,
\(\textcolor{#cc071e}{k}\): 1 roter Würfel wird entnommen,
\(\textcolor{#89ba17}{N - K}\): 3 grüne Würfel sind in der Urne und
\(\textcolor{#89ba17}{n - k}\): 1 grüner Würfel wird entnommen.
Die Wahrscheinlichkeit dafür, dass ein roter und ein grüner Würfel entnommen werden, kann somit mit dem Term \(\dfrac{\textcolor{#cc071e}{\displaystyle \binom{2}{1}} \cdot \textcolor{#89ba17}{\displaystyle \binom{3}{1}}}{\displaystyle \binom{5}{2}}\) angeben werden.
Anmerkung:
Es ist ebenso möglich \(K\) bzw. \(k\) die grünen Würfel und \(N - K\) bzw. \(n - k\) die roten Würfel zuzuordnen.
2. Möglichkeit: Laplace-Wahrscheinlichkeit
Laplace-Wahrscheinlichkeit eines Ereignisses \(A\)
\[P(A) = \frac{\vert A \vert}{\vert \Omega \vert} = \frac{\text{Anzahl der für} \; A \; \text{günstigen Ergebnisse}}{\text{Anzahl der möglichen Ergebnisse}}\]
Voraussetzung: Alle Ergebnisse (alle Versuchsausgänge) des betrachteten Zufallsexperiments sind gleichwahrscheinlich (Laplace-Experiment).
Das vorliegende Zufallsexperiment „Der Urne werden mit einem Griff zwei Würfel zufällig entnommen" unterscheidet die Ergebnisse
„Beide entnommenen Würfel sind rot.",
„Beide entnommenen Würfel sind grün" und
„Einer der entnommenen zwei Würfel ist rot, einer ist grün."
Da jedes der drei möglichen Ergebnisse mit \(p = \frac{1}{3}\) gleichwahrscheinlich ist, liegt ein Laplace-Experiment vor.
Binomialkoeffizient
Der Binomialkoeffizient gibt an, wie viele Möglichkeiten es gibt, aus einer Menge mit \(n\) Elementen eine Teilmenge mit \(k\) Elementen zu bilden.
\[\binom{n}{k} = \frac{n!}{k! \cdot (n - k)!} = \frac{n \cdot (n - 1) \cdot ... \cdot (n - k + 1)}{k!}\]
(vgl. Merkhilfe)
Es gibt \(\displaystyle \binom{5}{2}\) Möglichkeiten von 5 Würfeln 2 Würfel mit einem Griff zu entnehmen.
Es gibt \(\textcolor{#cc071e}{\displaystyle \binom{2}{1}}\) Möglichkeiten von 2 roten Würfeln 1 roten Würfel zu entnehmen.
Es gibt \(\textcolor{#89ba17}{\displaystyle \binom{3}{1}}\) Möglichkeiten von 3 grünen Würfeln 1 grünen Würfel zu entnehmen.
Dann gibt es \(\displaystyle \textcolor{#cc071e}{\binom{2}{1}} \cdot \textcolor{#89ba17}{\binom{3}{1}}\) günstige Möglichkeiten für das Ereignis: „1 roter und 1 grüner Würfel werden entnommen."
Die Wahrscheinlichkeit dafür, dass ein roter und ein grüner Würfel entnommen werden, lässt sich damit durch folgenden Term angeben:
\[\dfrac{\overbrace{\textcolor{#cc071e}{\displaystyle \binom{2}{1}} \cdot \textcolor{#89ba17}{\displaystyle \binom{3}{1}}}^{\text{Anzahl der günstigen Möglichkeiten}}}{\underbrace{\displaystyle \binom{5}{2}}_{\text{Anzahl aller Möglichkeiten}}}\]
3. Möglichkeit: Baumdiagramm, Pfadregeln
Im Folgenden wird das vorliegende Zufallsexperiment „Der Urne werden mit einem Griff zwei Würfel zufällig entnommen" als zweistufiges Zufallsexperiment nach dem Urnenmodell „Ziehen ohne Zurücklegen und ohne Beachtung der Reihenfolge" aufgefasst, bei dem die beiden Würfel nacheinander entnommen werden.
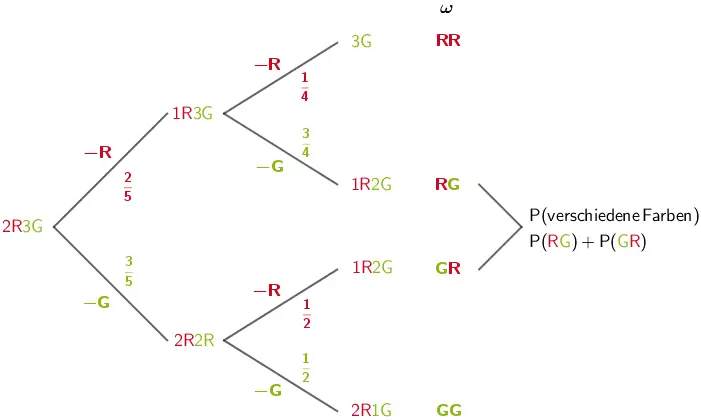
Das Baumdiagramm veranschaulicht den Anfangszustand der Urne sowie die Zustände nach der ersten und zweiten Stufe.
Dabei bedeutet \(\textcolor{#cc071e}{R}\): roter Würfel, \(\textcolor{#89ba17}{G}\): grüner Würfel, \(\textcolor{#cc071e}{-R}\): roter Würfel wird entnommen und \(\textcolor{#89ba17}{-G}\): grüner Würfel wird entnommen.
Mithilfe der ersten und der zweiten Pfadregel ergibt sich die Berechnung der Wahrscheinlichkeit für das Ereignis „Ein roter Würfel und ein grüner Würfel werden entnommen" (verschiedene Farben) wie folgt:
Pfadregeln
Verzweigungsregel (Knotenregel)
Die Summe der Wahrscheinlichkeiten an den Ästen, die von einem Knoten ausgehen, ist gleich eins.
1. Pfadregel (Produktregel)
Die Wahrscheinlichkeit eines Ergebnisses ist gleich dem Produkt der Wahrscheinlichkeiten entlang des Pfades, der zu dem Ergebnis führt.
2. Pfadregel (Summenregel)
Die Wahrscheinlichkeit eines Ereignisses ist gleich der Summe der Wahrscheinlichkeiten der Ergebnisse, die zu diesem Ereignis gehören.
\[\begin{align*}P(\text{verschiedene Farben}) &= \underbrace{P(\textcolor{#cc071e}{R}\textcolor{#89ba17}{G}) + P(\textcolor{#89ba17}{G}\textcolor{#cc071e}{R})}_{\large{\text{2. Pfadregel}}} \\[0.8em] &= \underbrace{\textcolor{#cc071e}{\frac{2}{5}} \cdot \textcolor{#89ba17}{\frac{3}{4}}}_{\large{\text{1. Pfadregel}}} + \underbrace{\textcolor{#89ba17}{\frac{3}{5}} \cdot \textcolor{#cc071e}{\frac{1}{2}}}_{\large{\text{1. Pfadregel}}}\end{align*}\]


