Der Freizeitpark veranstaltet ein Glücksspiel, bei dem Eintrittskarten für den Freizeitpark gewonnen werden können. Zu Beginn des Spiels wirft man einen Würfel, dessen Seiten mit den Zahlen 1 bis 6 durchnummeriert sind. Erzielt man dabei die Zahl 6, darf man anschließend einmal an einem Glücksrad mit drei Sektoren drehen (vgl. schematische Abbildung). Wird Sektor K erzielt, gewinnt man eine Kinderkarte im Wert von 28 Euro, bei Sektor E eine Erwachsenenkarte im Wert von 36 Euro. Bei Sektor N geht man leer aus. Der Mittelpunktswinkel des Sektors N beträgt 160°. Die Größen der Sektoren K und E sind so gewählt, dass pro Spiel der Gewinn im Mittel drei Euro beträgt. Bestimmen Sie die Größe der Mittelpunktswinkel der Sektoren K und E.
(6 BE)
Lösung zu Teilaufgabe 3
Betrachtung des Glücksrads:
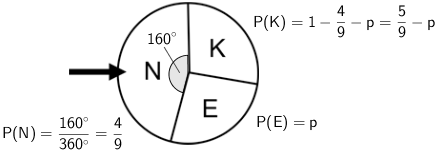
Anhand des Mittelpunktswinkel von Sektor N errechnet sich die Wahrscheinlichkeit \(P(N) = \dfrac{4}{9}\). Für den Sektor E wird beispielsweise die unbekannte Wahrscheinlichkeit \(P(E) = p\) gewählt. Da die Summe der Wahrscheinlichkeiten, einen der drei Sektoren zu erzielen, gleich eins ist, folgt \(P(K) = \dfrac{5}{9} - p\).
Es sei \(G\) die Zufallsgröße, welche jedem Ergebnis des Glücksspiels einen Gewinn in Euro zuordnet.
Da der Gewinn im Mittel drei Euro beträgt (vgl. Angabe), gilt für den Erwartungswert der Zufallsgröße \(G\):
Ist \(X\) eine Zufallsgröße, deren mögliche Werte \(x_{1}, x_{2}, ..., x_{n}\) sind, dann gilt:
Erwartungswert \(\boldsymbol{\mu}\) einer Zufallsgröße \(\boldsymbol{X}\)
\[\begin{align*}\mu = E(X) &= \sum \limits_{i = 1}^{n} x_{i} \cdot P(X = x_i) \\[0.8em] &= x_{1} \cdot P(X = x_1) + x_{2} \cdot P(X = x_2) + \cdots + x_{n} \cdot P(X = x_n) \end{align*}\]
Der Erwartungswert \(\mu = E(X)\) gibt den Mittelwert einer Zufallsgröße \(X\) pro Versuch an, der bei sehr häufiger Durchführung eines Zufallsexperiments (auf lange Sicht) zu erwarten ist.
\[E(G) = 3\]
Veranschaulichung des Glücksspiels als Baumdiagramm:
Es wird angenommen, dass es sich bei dem „Würfel" (vgl. Angabe) um einen Laplace-Würfel handelt (Bitte Anmerkung beachten).
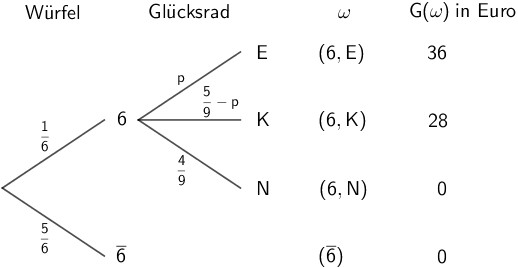
Mithilfe der Pfadregeln ergibt sich folgende Wagrscheinlichkeitsverteilung der Zufallsgröße \(G\):
Pfadregeln
Verzweigungsregel (Knotenregel)
Die Summe der Wahrscheinlichkeiten an den Ästen, die von einem Knoten ausgehen, ist gleich eins.
1. Pfadregel (Produktregel)
Die Wahrscheinlichkeit eines Ergebnisses ist gleich dem Produkt der Wahrscheinlichkeiten entlang des Pfades, der zu dem Ergebnis führt.
2. Pfadregel (Summenregel)
Die Wahrscheinlichkeit eines Ereignisses ist gleich der Summe der Wahrscheinlichkeiten der Ergebnisse, die zu diesem Ereignis gehören.
| \(\omega\) | \((6,N); (\overline{6})\) | \((6,K)\) | \((6,E)\) |
| \(G = g_{i}\) | \(\textcolor{#e9b509}{0}\) | \(\textcolor{#0087c1}{28}\) | \(\textcolor{#cc071e}{36}\) |
| \(P(G = g_{i})\) | \(\frac{1}{6} \cdot \frac{4}{9} + \frac{5}{6} = \textcolor{#e9b509}{\frac{49}{54}}\) | \(\textcolor{#0087c1}{\frac{1}{6}\cdot \left( \frac{5}{9} - p \right)}\) | \(\textcolor{#cc071e}{\frac{1}{6}\cdot p}\) |
Mit \(E(G) = 3\) folgt:
Ist \(X\) eine Zufallsgröße, deren mögliche Werte \(x_{1}, x_{2}, ..., x_{n}\) sind, dann gilt:
Erwartungswert \(\boldsymbol{\mu}\) einer Zufallsgröße \(\boldsymbol{X}\)
\[\begin{align*}\mu = E(X) &= \sum \limits_{i = 1}^{n} x_{i} \cdot P(X = x_i) \\[0.8em] &= x_{1} \cdot P(X = x_1) + x_{2} \cdot P(X = x_2) + \cdots + x_{n} \cdot P(X = x_n) \end{align*}\]
Der Erwartungswert \(\mu = E(X)\) gibt den Mittelwert einer Zufallsgröße \(X\) pro Versuch an, der bei sehr häufiger Durchführung eines Zufallsexperiments (auf lange Sicht) zu erwarten ist.
\[\begin{align*}\textcolor{#e9b50e}{0} \cdot \textcolor{#e9b509}{\frac{49}{54}} + \textcolor{#0087c1}{28} \cdot \textcolor{#0087c1}{\frac{1}{6}\cdot \left( \frac{5}{9} - p \right)} + \textcolor{#cc071e}{36} \cdot \textcolor{#cc071e}{\frac{1}{6} \cdot p} &= 3 \\[0.8em] \frac{1}{6} \cdot \left[ 28 \cdot \left( \frac{5}{9} - p \right) + 36p \right] &= 3 &&| \cdot 6 \\[0.8em] 28 \cdot \frac{5}{9} - 28p + 36p &= 18 \\[0.8em] \frac{140}{9} + 8p &= 18 &&| - \frac{140}{9} \\[0.8em] 8p &= \frac{22}{9} &&| : 8 \\[0.8em] p &= \frac{11}{36}\end{align*}\]
\[\Rightarrow \enspace P(E) = p = \frac{11}{36}\]
\[\Rightarrow \enspace P(K) = \frac{5}{9} - p = \frac{5}{9} - \frac{11}{36} = \frac{1}{4}\]
Größe der Mittelpunktswinkel der Sektoren E und K bestimmen:
\[P(E) \cdot 360^{\circ} = \frac{11}{36} \cdot 360^{\circ} = 110^{\circ}\]
\[P(K) \cdot 360^{\circ} = \frac{1}{4} \cdot 360^{\circ} = 90^{\circ}\]
Die Größe des Mittelpunktswinkels des Sektors E beträgt 110° und die des Sektors K beträgt 90°.
Auch wenn bei dieser Aufgabe - im Gegensatz zu vergleichbaren Abituraufgaben - nicht ausdrücklich von einem Laplace-Würfel oder idealen Würfel die Rede ist, ist es sinnvoll, vom naheliegendsten Fall eines Laplace-Würfels auszugehen.
Dennoch darf sich die Aufgabenstellung den Vorwurf einer unnötig interpretierbaren Formulierung gefallen lassen, weshalb unter anderem diese Aufgabe im Rahmen der Petition zum Mathematik Abitur Bayern 2021 bzw. der Analyse der Prüfungsangaben in die Kritik geraten ist.


