Geben Sie den Term einer in \(\mathbb R\) definierten Funktion \(f\) an, sodass die in \(\mathbb R\) definierte Integralfunktion \(\displaystyle F \colon x \mapsto \int_{-1}^x f(t)\,dt\) genau zwei Nullstellen besitzt. Geben Sie die Nullstellen von \(F\) an.
(3 BE)
Lösung zu Teilaufgabe 4b
\[F(x) = \int_{-1}^x f(t)\,dt\,; \quad D_F = \mathbb R\]
1. Nullstelle von \(F\)
Nullstelle einer Integralfunktion
Jede Integralfunktion \(\displaystyle I_{a} \colon x \mapsto \int_{a}^{x} f(t)\, dt\) besitzt an der unteren Integrationsgrenze \(x = a\) eine Nullstelle.
\[I_{a}(a) = \int_{a}^{a} f(t) \, dt = F(a) - F(a) = 0\]
\(F\) ist eine Stammfunktion von \(f\).
Die Integralfunktion \(\displaystyle F(x) = \int_{-1}^x f(t)\,dt\) hat unabhängig vom Term der Intgrandenfunktion \(f\) eine Nullstelle an der unteren Integrationsgrenze.
\[F(-1) = \int_{-1}^{-1} f(t)\,dt = 0\]
2. Nullstelle von \(F\)
Die Integralfunktion \(F\) einer zum Ursprung punktsymmetrische Integrandenfunktion \(f\), hat an der Stelle \(x = 1\) eine zweite Nullstelle. Wegen der Punktsymmetrie \(f(-t) = -f(t)\) verläuft der Graph von \(f\) in den Teilintervallen \([-1;0[\) und \(]0;1]\) einmal unterhalb und einmal oberhalb der \(x\)-Achse. Die Flächeninhalte der Flächenstücke, die \(G_f\) in den Teilintervallen \([-1;0[\) und \(]0;1]\) mit der \(x\)-Achse einschließt, sind dem Betrag nach gleich groß, gehen in die Berechnung der Flächenbilanz \(\displaystyle \int_{-1}^1 f(t)\,dt\) aber mit unterschiedlichem Vorzeichen ein. Somit ist die Flächenbilanz gleich Null.
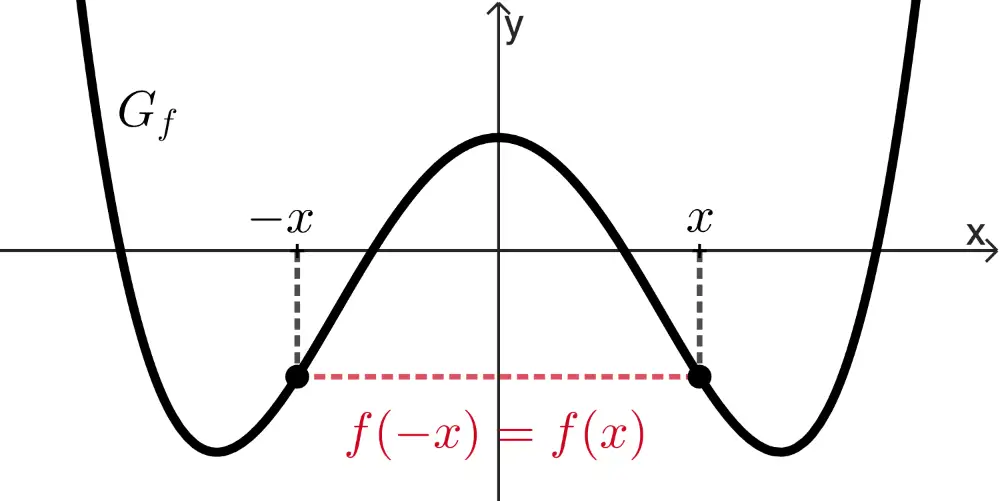
Symmetrie von Funktionsgraphen bzgl. des Koordinatensystems
Der Graph einer Funktion \(f\) ist
achsensymmetrisch bzgl. der \(\boldsymbol{y}\)-Achse,
wenn für alle \(x \in D_f\) gilt: \(f(-x) = f(x)\).
punktsymmetrisch bzgl. des Koordinatenursprungs,
wenn für alle \(x \in D_f\) gilt: \(f(-x) = -f(x)\)
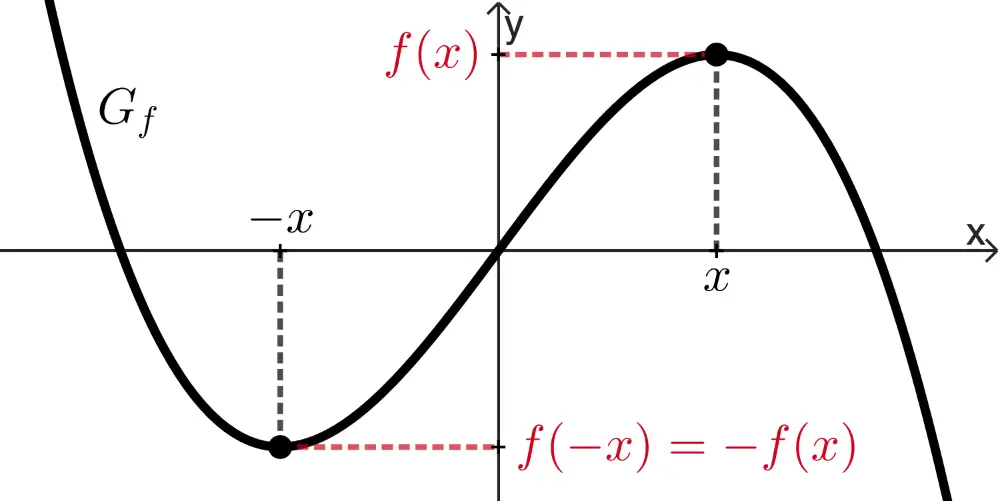
\[F(1) = \int_{-1}^1 f(t)\,dt = \int_{-1}^0 f(t)\,dt + \int_0^1 f(t)\,dt = 0\]
wobei gilt: \(\,f(-t) = -f(t)\,\) (Punktsymmetrie)
Da die Intergalfunktion genau zwei Nullstellen besitzen soll, wählt man sicherheitshalber eine punktsymmetrische Integrandenfunktion\(f\), welche in \(\mathbb R\) monoton steigt (fällt) bzw. für \(x > 1\) keine Nullstellen mit Vorzeichenwechsel besitzt (siehe Anmerkung).
Beispiel A
\[f(t) = t\,; \quad D_f = \mathbb R\]
Punktsymmetrie von \(f\):
Symmetrie von Funktionsgraphen bzgl. des Koordinatensystems
Der Graph einer Funktion \(f\) ist
achsensymmetrisch bzgl. der \(\boldsymbol{y}\)-Achse,
wenn für alle \(x \in D_f\) gilt: \(f(-x) = f(x)\).
punktsymmetrisch bzgl. des Koordinatenursprungs,
wenn für alle \(x \in D_f\) gilt: \(f(-x) = -f(x)\)
\[f(-t) = -t = -f(t)\]
2. Nullstelle von \(F\):
Stammfunktion einer Potenzfunktion
\[f(x) = x^r \quad \Longrightarrow \quad F(x) = \frac{1}{r + 1} \cdot x^{r + 1} + C\]
\[r \neq -1\]
Berechnung bestimmter Integrale
\[\int_{a}^{b} f(x)\,dx = [F(x)]_{a}^{b} = F(b) - F(a)\]
Dabei ist \(F\) eine beliebige Stammfunktion zu \(f\).
(vgl. Merkhilfe)
Eigenschaften des bestimmten Integrals - Integrationsregeln
Identische Integrationsgrenzen:
\[\int_{a}^{a} f(x)\,dx = 0\]
Faktorregel:
\(\displaystyle \int_{a}^{b} c \cdot f(x)\,dx = c \cdot \int_{a}^{b} f(x)\,dx\) mit \(c \in \mathbb R\)
Summenregel:
\[\int_{a}^{b} \left[f(x) \pm g(x) \right] dx = \int_{a}^{b}f(x)\,dx \pm \int_{a}^{b}g(x)\,dx\]
Vertauschungsregel:
\[\int_{a}^{b}f(x)\,dx = -\int_{b}^{a}f(x)\,dx\]
Zerlegung in Teilintervalle:
\(\displaystyle \int_{a}^{b}f(x)\,dx = \int_{a}^{c}f(x)\,dx + \int_{c}^{b}f(x)\,dx\) mit \(a \leq c \leq b\)
\[\begin{align*} F(1) &= \int_{-1}^1 t\,dt \\[0.8em] &= \left[ \frac{1}{2}t^2 \right]_{-1}^1 \\[0.8em] &= \frac{1}{2} \cdot 1^2 - \left( \frac{1}{2} \cdot (-1)^2 \right) \\[0.8em] &= \frac{1}{2} - \frac{1}{2} \\[0.8em] &= 0 \end{align*}\]
weitere Nullstellen:
Anwendung der Differetialrechnung:
Monotoniekriterium
\(\textcolor{#cc071e}{f'(x) < 0}\) im Intervall \( I \; \Rightarrow \; G_{f}\) fällt streng monoton in \(I\)
\(\textcolor{#0087c1}{f'(x) > 0}\) im Intervall \( I \; \Rightarrow \; G_{f}\) steigt streng monoton in \(I\)
(vgl. Merkhilfe)
Ableitung einer Potenzfunktion
\[f(x) = x^r \quad \Longrightarrow \quad f'(x) = rx^{r - 1} \quad (r \in \mathbb R)\]
(vgl. Merkhilfe)
\[f(t) = t \quad \Longrightarrow \quad f'(t) = 1 \quad \Longrightarrow \quad f'(t) > 0\]
Da \(G_f\) für \(x > 1\) streng monoton steigt, kann es keine weiteren Nullstellen von \(F\) geben.
\(\Longrightarrow \quad\) Genau zwei Nullstellen: \(\, x_1 = -1\,; \enspace x_2 = 1\)
![Graph der Punktsymmetrische Integrandenfunktion f(t) = t, Flächenbilanz Integralfunktion F im Intervall [-1;1]](/images/stories/B2012_A_II/B2012_A_II_T_1_4_01.png "Grafik 1 zur Lösung der Teilaufgabe 4b - Analysis II Teil 1 - Mathematik Abitur Bayern 2012")
Die in \(\,\mathbb R\,\) definierte Integralfunktion \(\displaystyle \,F(x) = \int_{-1}^x f(t)\,dt\,\) der zum Ursprung punktsymmetrischen, in \(\,\mathbb R\,\) streng monoton steigenden Intergrandenfunktion \(\,f(t) = t\,\) hat die Nullstelle \(\,x = 1\,\). Die Flächenbilanz des bestimmten Integrals \(\displaystyle \int_{-1}^1 f(t)\,dt\,\) ist gleich Null.
Beispiel B
\[f(t) = t^3\,; \quad D_f = \mathbb R\]
Punktsymmetrie von \(f\,\):
Symmetrie von Funktionsgraphen bzgl. des Koordinatensystems
Der Graph einer Funktion \(f\) ist
achsensymmetrisch bzgl. der \(\boldsymbol{y}\)-Achse,
wenn für alle \(x \in D_f\) gilt: \(f(-x) = f(x)\).
punktsymmetrisch bzgl. des Koordinatenursprungs,
wenn für alle \(x \in D_f\) gilt: \(f(-x) = -f(x)\)
\[f(-t) = (-t)^3 = -t^3 = -f(t)\]
2. Nullstelle von \(F\,\):
Stammfunktion einer Potenzfunktion
\[f(x) = x^r \quad \Longrightarrow \quad F(x) = \frac{1}{r + 1} \cdot x^{r + 1} + C\]
\[r \neq -1\]
Berechnung bestimmter Integrale
\[\int_{a}^{b} f(x)\,dx = [F(x)]_{a}^{b} = F(b) - F(a)\]
Dabei ist \(F\) eine beliebige Stammfunktion zu \(f\).
(vgl. Merkhilfe)
Eigenschaften des bestimmten Integrals - Integrationsregeln
Identische Integrationsgrenzen:
\[\int_{a}^{a} f(x)\,dx = 0\]
Faktorregel:
\(\displaystyle \int_{a}^{b} c \cdot f(x)\,dx = c \cdot \int_{a}^{b} f(x)\,dx\) mit \(c \in \mathbb R\)
Summenregel:
\[\int_{a}^{b} \left[f(x) \pm g(x) \right] dx = \int_{a}^{b}f(x)\,dx \pm \int_{a}^{b}g(x)\,dx\]
Vertauschungsregel:
\[\int_{a}^{b}f(x)\,dx = -\int_{b}^{a}f(x)\,dx\]
Zerlegung in Teilintervalle:
\(\displaystyle \int_{a}^{b}f(x)\,dx = \int_{a}^{c}f(x)\,dx + \int_{c}^{b}f(x)\,dx\) mit \(a \leq c \leq b\)
\[\begin{align*} F(1) &= \int_{-1}^1 t^3\,dt \\[0.8em] &= \left[ \frac{1}{4}t^4 \right]_{-1}^1 \\[0.8em] &= \frac{1}{4} \cdot 1^4 - \left( \frac{1}{4} \cdot (-1)^4 \right) \\[0.8em] &= \frac{1}{4} - \frac{1}{4} \\[0.8em] &= 0 \end{align*}\]
weitere Nullstellen:
Anwendung der Differetialrechnung:
Monotoniekriterium
\(\textcolor{#cc071e}{f'(x) < 0}\) im Intervall \( I \; \Rightarrow \; G_{f}\) fällt streng monoton in \(I\)
\(\textcolor{#0087c1}{f'(x) > 0}\) im Intervall \( I \; \Rightarrow \; G_{f}\) steigt streng monoton in \(I\)
(vgl. Merkhilfe)
Ableitung einer Potenzfunktion
\[f(x) = x^r \quad \Longrightarrow \quad f'(x) = rx^{r - 1} \quad (r \in \mathbb R)\]
(vgl. Merkhilfe)
\[f(t) = t^3 \quad \Longrightarrow \quad f'(t) = 3t^2 \quad \Longrightarrow \quad f'(t) > 0\]
Da \(G_f\) für \(x > 1\) streng monoton steigt, kann es keine weiteren Nullstellen von \(F\) geben.
\(\Longrightarrow \quad\) Genau zwei Nullstellen: \(\, x_1 = -1\,; \enspace x_2 = 1\)
![Graph der Punktsymmetrische Integrandenfunktion f(t) = t³, Flächenbilanz Integralfunktion F im Intervall [-1;1]](/images/stories/B2012_A_II/B2012_A_II_T_1_4_03.png "Grafik 2 zur Lösung der Teilaufgabe 4b - Analysis II Teil 1 - Mathematik Abitur Bayern 2012")
Die in \(\,\mathbb R\,\) definierte Integralfunktion \(\displaystyle F(x) = \int_{-1}^x f(t)\,dt\,\) der zum Ursprung punktsymmetrischen, in \(\,\mathbb R\,\) monoton steigenden Intergrandenfunktion \(\,f(t) = t^3\,\) hat die Nullstelle \(\,x = 1\,\). Die Flächenbilanz des bestimmten Integrals \(\displaystyle \int_{-1}^1 f(t)\,dt\,\) ist gleich Null.
Beispiel C
\[f(t) = t^3 - t\,; \quad D_f = \mathbb R\]
Punktsymmetrie von \(f\,\):
Symmetrie von Funktionsgraphen bzgl. des Koordinatensystems
Der Graph einer Funktion \(f\) ist
achsensymmetrisch bzgl. der \(\boldsymbol{y}\)-Achse,
wenn für alle \(x \in D_f\) gilt: \(f(-x) = f(x)\).
punktsymmetrisch bzgl. des Koordinatenursprungs,
wenn für alle \(x \in D_f\) gilt: \(f(-x) = -f(x)\)
\[f(-t) = (-t)^3 - (-t) = -t^3 + t = -(t^3 - t) = -f(t)\]
2. Nullstelle von \(F\,\):
Stammfunktion einer Potenzfunktion
\[f(x) = x^r \quad \Longrightarrow \quad F(x) = \frac{1}{r + 1} \cdot x^{r + 1} + C\]
\[r \neq -1\]
Berechnung bestimmter Integrale
\[\int_{a}^{b} f(x)\,dx = [F(x)]_{a}^{b} = F(b) - F(a)\]
Dabei ist \(F\) eine beliebige Stammfunktion zu \(f\).
(vgl. Merkhilfe)
Eigenschaften des bestimmten Integrals - Integrationsregeln
Identische Integrationsgrenzen:
\[\int_{a}^{a} f(x)\,dx = 0\]
Faktorregel:
\(\displaystyle \int_{a}^{b} c \cdot f(x)\,dx = c \cdot \int_{a}^{b} f(x)\,dx\) mit \(c \in \mathbb R\)
Summenregel:
\[\int_{a}^{b} \left[f(x) \pm g(x) \right] dx = \int_{a}^{b}f(x)\,dx \pm \int_{a}^{b}g(x)\,dx\]
Vertauschungsregel:
\[\int_{a}^{b}f(x)\,dx = -\int_{b}^{a}f(x)\,dx\]
Zerlegung in Teilintervalle:
\(\displaystyle \int_{a}^{b}f(x)\,dx = \int_{a}^{c}f(x)\,dx + \int_{c}^{b}f(x)\,dx\) mit \(a \leq c \leq b\)
\[\begin{align*} F(1) &= \int_{-1}^1 \big(t^3 - t\big)\,dt \\[0.8em] &= \left[ \frac{1}{4}t^4 - \frac{1}{2}t^2 \right]_{-1}^1 \\[0.8em] &= \frac{1}{4} \cdot 1^4 -\frac{1}{2} \cdot 1^2 - \left( \frac{1}{4} \cdot (-1)^4 - \frac{1}{2} \cdot (-1)^2 \right) \\[0.8em] &= -\frac{1}{4} + \frac{1}{4} \\[0.8em] &= 0 \end{align*}\]
weitere Nullstellen:
Anwendung der Differetialrechnung:
Monotoniekriterium
\(\textcolor{#cc071e}{f'(x) < 0}\) im Intervall \( I \; \Rightarrow \; G_{f}\) fällt streng monoton in \(I\)
\(\textcolor{#0087c1}{f'(x) > 0}\) im Intervall \( I \; \Rightarrow \; G_{f}\) steigt streng monoton in \(I\)
(vgl. Merkhilfe)
Ableitung einer Potenzfunktion
\[f(x) = x^r \quad \Longrightarrow \quad f'(x) = rx^{r - 1} \quad (r \in \mathbb R)\]
(vgl. Merkhilfe)
\(f(t) = t^3 - t \quad \Longrightarrow \quad f'(t) = 3t^2 - 1 \quad \Longrightarrow \quad f'(t) > 0\) für \(x > 1\)
Da \(G_f\) für \(x > 1\) streng monoton steigt, kann es keine weiteren Nullstellen von \(F\) geben.
\(\Longrightarrow \quad\) Genau zwei Nullstellen: \(\, x_1 = -1\,; \enspace x_2 = 1\)
![Graph der punktsymmetrischen Integrandenfunktion f(t) = t³ - t, Flächenbilanz der Integralfunktion F im Intervall [-1;1]](/images/stories/B2012_A_II/B2012_A_II_T_1_4_05.png "Grafik 3 zur Lösung der Teilaufgabe 4b - Analysis II Teil 1 - Mathematik Abitur Bayern 2012")
Die in \(\,\mathbb R\,\) definierte Integralfunktion \(\displaystyle F(x) = \int_{-1}^x f(t)\,dt\,\) der zum Ursprung punktsymmetrischen, in \(\,\mathbb R\,\) monoton steigenden Intergrandenfunktion \(\,f(t) = t^3 - t\,\) hat die Nullstelle \(\,x = 1\,\). Die Flächenbilanz des bestimmten Integrals \(\displaystyle \int_{-1}^1 f(t)\,dt\,\) ist gleich Null.
Anmerkung
Folgende zwei Beispiele zeigen in \(\mathbb R\) definierte Integralfunktionen \(F\,\) von in \(\mathbb R\) definierten, punktsymmetrischen Integrandenfunktion \(f\), die mehr als zwei Nullstellen besitzen.
1. Beispiel: \(\,\displaystyle F(x) = \int_{-1}^x \sin(t)\,dt\)
![Graph der Punktsymmetrische Integrandenfunktion f(t) = sin(t), Flächenbilanz der Integralfunktion F im Intervall [-1;2π + 1]](/images/stories/B2012_A_II/B2012_A_II_T_1_4_02b.png)
Aufgrund der Periodizität der Sinusfunktion, besitzt die in \(\,\mathbb R\,\) definierte Integralfunktion \(\displaystyle F(x) = \int_{-1}^x \sin(t)\,dt\,\) beliebig viele Nullstellen für \(x = 2k\pi + 1\,, \enspace k \in \mathbb Z\,\).
2. Beispiel: \(\displaystyle F(x) = \int_{-1}^x \big( t^5 - t^3 - t \big)\,dt\)
![Graph der punktsymmetrischen Integrandenfunktion f(t) = t⁵ - t³ - t, Flächenbilanz der Integralfunktion F im Intervall [-1;1]](/images/stories/B2012_A_II/B2012_A_II_T_1_4_04.png "Grafik 5 zur Lösung der Teilaufgabe 4b - Analysis II Teil 1 - Mathematik Abitur 2012")
Die Integralfunktion \(\displaystyle F(x) = \int_{-1}^x \big( t^5 - t^3 - t \big)\,dt\,\) besitzt eine dritte Nullstelle für \(\,x \approx 1{,}46\,\). Die Flächenbilanz für \(\displaystyle \int_{-1}^1 \big( t^5 - t^3 - 1 \big)\,dt\,\) sowie die Flächenbilanz für \(\displaystyle \int_1^{1{,}46} \big( t^5 - t^3 - t \big)\,dt\,\) ist jeweils gleich Null. Somit ist die Flächenbilanz für \(\displaystyle \int_{-1}^{1{,}46} \big( t^5 - t^3 - t \big)\,dt\,\) ebenfalls gleich Null.
