Die Abbildung zeigt einen Würfel \(ABCDEFGH\) der Kantenlänge 4 in einem Koordinatensystem. Drei Seitenflächen dieses Würfels liegen in Koordinatenebenen.
Die Ebene \(K\) enthält die Punkte \(A(0|0|0)\), \(B(4|0|0)\) und den Mittelpunkt der Kante \([FG]\).
Die Ebene \(K\) teilt den Würfel in zwei Teilkörper. Berechnen Sie das Volumen des kleineren Teilkörpers.

(2 BE)
Lösung zu Teilaufgabe a
Volumen eines geraden Prismas (vgl. Merkhilfe)
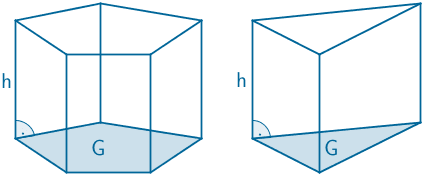
\[V_{\text{Prisma}} = G \cdot h\]
Der kleinere Teilkörper ist ein gerades Prisma mit einem rechtwinkligen Dreieck der Seitenlängen 4 und 2 als Grund- und Deckfläche. Die Höhe des Prismas entspricht der Kantenlänge 4 des Würfels \(ABCDEFGH\).
\[V_{\text{Prisma}}= \textcolor{#e9b509}{g} \cdot \textcolor{#0087c1}{h} = \textcolor{#e9b509}{\frac{1}{2} \cdot 4 \cdot 2} \cdot \textcolor{#0087c1}{4} = 16\]

Alternative:
Der Würfel lässt sich in vier kongruente Prismen zerlegen.
\[V_{\text{Prisma}} = \frac{1}{4} \cdot V_{\text{Würfel}} = \frac{1}{4} \cdot 4^3 = 16\]



