Gegeben ist die in \(\mathbb R\) definierte Funktion \(g \colon x \mapsto x^2-e^x\). Der Graph von \(g\) besitzt genau einen Wendepunkt \(W\). Bestimmen Sie rechnerisch die \(x\)-Koordinate von \(W\) und beurteilen Sie, ob \(W\) oberhalb der \(x\)-Achse liegt.
(5 BE)
Lösung zu Teilaufgabe 2
\[g(x) = x^2 - e^x; \; D_g = \mathbb R\]
Wendestelle des Graphen von \(g\)
Die notwendige Bedingung für eine Wendestelle von \(g\) lautet \(g''(x) = 0\).
Wendestellen(n)
Ist eine Funktion \(f\) in einem Intervall \(I =\, ]a;b[\) zweimal differenzierbar und \(x_0\) eine innere Stelle von \(I\), so gilt:
Die Stelle \(x_0\) ist genau dann eine Wendestelle von \(f\), wenn \(f''(x_0) = 0\) ist und \(f''\) an der Stelle \(x_0\) das Vorzeichen wechselt.
Wendestelle(n) und dritte Ableitung
Ist eine Funktion \(f\) in einem Intervall \(I =\, ]a;b[\) dreimal differenzierbar und \(x_0\) eine innere Stelle von \(I\), so gilt:
Die Stelle \(x_0\) ist eine Wendestelle von \(f\), wenn \(f''(x_0) = 0\) ist und \(f'''(x_0) \neq 0\) ist.
Zweite Ableitungsfunktion \(g''\) bilden:
Ableitungen der Grundfunktionen
\[c' = 0 \enspace (c \in \mathbb R)\]
\[\left( x^r \right)' = r \cdot x^{r - 1} \enspace (r \in \mathbb R)\]
\[\left( \sqrt{x} \right)' = \frac{1}{2\sqrt{x}}\]
\[\left( \sin{x} \right)' = \cos{x}\]
\[\left( \cos{x} \right)' = -\sin{x}\]
\[\left( \ln{x} \right)' = \frac{1}{x}\]
\[\left( \log_{a}{x}\right)' = \frac{1}{x \cdot \ln{a}}\]
\[\left( e^x \right)' = e^x\]
\[\left(a^x \right)' = a^x \cdot \ln{a}\]
Faktorregel
\[\begin{align*}f(x) &= a \cdot \textcolor{#0087c1}{u(x)} \\[0.8em] f'(x) &= a \cdot \textcolor{#0087c1}{u'(x)}\end{align*}\]
Summenregel
\[\begin{align*}f(x) &= \textcolor{#0087c1}{u(x)} + \textcolor{#cc071e}{v(x)} \\[0.8em] f'(x) &= \textcolor{#0087c1}{u'(x)} + \textcolor{#cc071e}{v'(x)}\end{align*}\]
Produktregel
\[\begin{align*}f(x) &= \textcolor{#0087c1}{u(x)} \cdot \textcolor{#cc071e}{v(x)} \\[0.8em] f'(x) &= \textcolor{#0087c1}{u'(x)} \cdot \textcolor{#cc071e}{v(x)} + \textcolor{#0087c1}{u(x)} \cdot \textcolor{#cc071e}{v'(x)}\end{align*}\]
Quotientenregel
\[\begin{align*}f(x) &= \dfrac{\textcolor{#0087c1}{u(x)}}{\textcolor{#cc071e}{v(x)}} \\[0.8em] f'(x) &= \dfrac{\textcolor{#0087c1}{u'(x)} \cdot \textcolor{#cc071e}{v(x)} - \textcolor{#0087c1}{u(x)} \cdot \textcolor{#cc071e}{v'(x)}}{[\textcolor{#cc071e}{v(x)}]^{2}}\end{align*}\]
Kettenregel
\[\begin{align*}f(x) &= \textcolor{#0087c1}{u(}\textcolor{#cc071e}{v(x)}\textcolor{#0087c1}{)} \\[0.8em] f'(x) &= \textcolor{#0087c1}{u'(}\textcolor{#cc071e}{v(x)}\textcolor{#0087c1}{)} \cdot \textcolor{#cc071e}{v'(x)}\end{align*}\]
\[g'(x) = 2x - e^x\]
\[g''(x) = 2 - e^x\]
Nullstelle von \(g''\) bestimmen:
\[\begin{align*}g''(x) &= 0 \\[0.8em] 2 - e^x &= 0 &&| +e^x \\[0.8em] 2 &= e^x &&|\; \ln\; \text{(Logarithmieren)} \\[0.8em] \ln{2} &= x \end{align*}\]
Da der Graph von \(g\) genau einen Wendepunkt besitzt (vgl. Angabe), ist \(x = \ln{2}\) die Wendestelle von \(g\).
Beurteilung, ob der Wendepunkt \(W\) oberhalb der \(x\)-Achse liegt
Es ist abzuschätzen, ob der Wert der \(y\)-Koordinate des Wendepunkts \(W(\ln{2}|g(\ln{2}))\) positiv oder negativ ist.
\[g(x) = x^2 - e^x\]
\[\begin{align*}g(\ln{2}) &= \left( \ln{2} \right)^2 - e^{\ln{2}} &&| \; e^{\ln{x}} = x \\[0.8em] &= \left( \ln{2} \right)^2 - 2\end{align*}\]
Wert von \(\left(\ln{2}\right)^2\) abschätzen:
Geeignete Vergleichswerte sind \(2 < e \approx 2{,}7\) sowie \(\ln{1} = 0\) (Jeder Logarithmus von eins ist null.) und \(\ln{e} = 1\). (Jeder Logarithmus von seiner eigenen Basis ist eins.)
Die natürliche Logarithmusfunktion \(x \mapsto \ln{x}\) ist auf ihrem Definitionsbereich \(D = \mathbb R^+\) streng monoton zunehmend.
Deshalb gilt \(0 = \ln{1} < \ln{2} < \ln{e} = 1\).
Dann hat auch \(\left( \ln{2}\right)^2\) einen Wert zwischen \(0\) und \(1\).
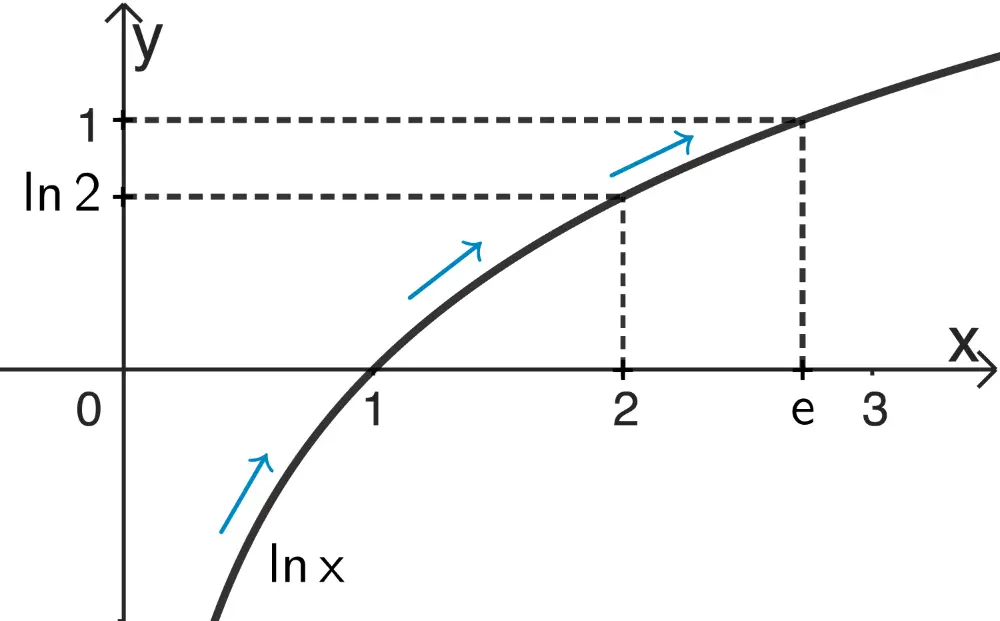ergänzende Darstellung
\[\textcolor{#cc071e}{g(\ln{2})} = \underbrace{\left( \ln{2} \right)^2}_{]0;1[} - 2 \textcolor{#cc071e}{< 0}\]
Da der Wert der \(y\)-Koordinate des Wendepunkts \(W(\ln{2}|\textcolor{#cc071e}{g(\ln{2})})\) negativ ist, liegt der Wendepunkt \(W\) des Graphen der Funktion \(g\) unterhalb der \(x\)-Achse.
